A point source is situated at a distance x<f from the pole of the concave mirror of focal length f. At time t=0 the point source starts moving away from the mirror with constant velocity. Which of the graphs below represents best, variation of image distance |v| with distance x between the pole of mirror and the source.


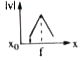
The correct Answer is:A
To solve the problem, we need to analyze the behavior of the image distance |v| as the object distance x changes when the point source moves away from the concave mirror. We will use the mirror formula and the properties of concave mirrors.
1. Understand the Setup:
- We have a concave mirror with a focal length f.
- The point source (object) is initially located at a distance x from the mirror, where x<f. This means the object is located between the mirror's pole and its focus.
2. Use the Mirror Formula:
- The mirror formula is given by:
1f=1v+1u
- Here, u is the object distance (which is negative for a concave mirror), and v is the image distance (which can be positive or negative depending on the position of the image).
3. Determine the Initial Conditions:
- Since the object is between the mirror's pole and focus, the object distance u=−x (negative because it's in front of the mirror).
- When the object is at this position, the image formed will be virtual and located behind the mirror.
4. Calculate the Image Distance:
- Rearranging the mirror formula gives us:
1v=1f−1u
- Substituting u=−x:
1v=1f+1x
- This implies:
v=fxx+f
- Since the image is virtual, we take the modulus |v|.
5. Analyze the Behavior as the Object Moves:
- As the object moves away from the mirror (increasing x), we note that |v| will change.
- When x approaches f, |v| approaches infinity (since the rays converge at the focus).
- When x is greater than f (the object moves beyond the focus), the image distance will start decreasing as the object distance increases further.
6. Graphical Representation:
- The graph of |v| vs. x will show that as x increases from a value less than f to f, |v| will increase towards infinity.
- After x exceeds f, |v| will decrease as the object moves further away from the mirror.
Conclusion:
The graph that best represents the variation of image distance |v| with the distance x is one that starts from a finite value (as x approaches f) and goes to infinity, then decreases as x continues to increase beyond f.
- We have a concave mirror with a focal length f.
- The point source (object) is initially located at a distance x from the mirror, where x<f. This means the object is located between the mirror's pole and its focus.
- The mirror formula is given by:
1f=1v+1u
- Here, u is the object distance (which is negative for a concave mirror), and v is the image distance (which can be positive or negative depending on the position of the image).
- Since the object is between the mirror's pole and focus, the object distance u=−x (negative because it's in front of the mirror).
- When the object is at this position, the image formed will be virtual and located behind the mirror.
- Rearranging the mirror formula gives us:
1v=1f−1u
- Substituting u=−x:
1v=1f+1x
- This implies:
v=fxx+f
- Since the image is virtual, we take the modulus |v|.
- As the object moves away from the mirror (increasing x), we note that |v| will change.
- When x approaches f, |v| approaches infinity (since the rays converge at the focus).
- When x is greater than f (the object moves beyond the focus), the image distance will start decreasing as the object distance increases further.
- The graph of |v| vs. x will show that as x increases from a value less than f to f, |v| will increase towards infinity.
- After x exceeds f, |v| will decrease as the object moves further away from the mirror.
The graph that best represents the variation of image distance |v| with the distance x is one that starts from a finite value (as x approaches f) and goes to infinity, then decreases as x continues to increase beyond f.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - PRACTICE SHEET (EXERCISE I LEVEL -II (ADVANCED) MORE THAN ONE CORRECT TYPE QUESTIONS)2videos
GEOMETRICAL OPTICS
- BOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - PRACTICE SHEET (EXERCISE I LEVEL -II (ADVANCED) LINKED COMPREHENSION TYPE QUESTIONS)6videos
GEOMETRICAL OPTICS
- BOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - PRACTICE SHEET (EXERCISE I LEVEL -I (MAIN) STRAIGHT OBJECTIVE TYPE QUESTIONS)11videos
GEOMETRICAL OPTICS
- BOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS10videos
ELEMENTS OF VECTORS
- BOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - PRACTICE EXERCISE106videos
LAWS OF MOTION
Similar Questions
An object is placed at a distance 20 cm from the pole of a convex mirror of focal length 20 cm. The image is produced at
View SolutionFind the nature of image when an object is placed at 2f from the pole of a convex mirror of focal length f
View SolutionFor a concave mirror of focal length f, image is 2 times larger. Then the object distance from the mirror can be
View SolutionAn object is placed at a distance f in the front of a convex mirror. If focal length of the mirror is f, then distance of image from pole of the mirror is
View SolutionA point object is placed at a distance 20 cm from the focus of a concave mirror of radius of curvature 20 cm. Find the distance (in cm) of the image from the focus.
View SolutionA point source of light is placed at a distance of 2f from a converging lens of focal length f. The intensity onteh other side of the lens is maximum at a distance
View SolutionThe image of an object placed on the principal axis of a concave mirror of focal length 12 cm is formed at a point which is 10cm more distance form the mirror than the object. The magnification of the image is
View SolutionAn infinitely long rod lies along the axis of a concave mirror of focal length f. The near end of the rod is distance u>f from the mirror. Its image will have length
View SolutionA convex mirror offocal length fforms an image which is 1/n times the object. The distance of the object from the mirror is:
View SolutionFind the distance of object from a concave mirror of focal length 10 cm so that image size is four time the size of the object.
View Solution

