A thin biconvex lens of focal length 6.25 cm is made of material of refractive index 1.5. It is cut into two identical pieces perpendicular to its principal axis. One of the pieces is placed in water of refractive index 43. The focal power of the piece immersed in water in diopter is
The correct Answer is:2
To find the focal power of the piece of the biconvex lens immersed in water, we will follow these steps:
Step 1: Understand the problem
We have a biconvex lens with a focal length of 6.25 cm and a refractive index of 1.5. When cut into two pieces, one piece is placed in water (refractive index = 4/3). We need to find the focal power of the piece in water.
Step 2: Use the Lens Maker's Formula
The Lens Maker's Formula is given by:
1f=(n2−n1)⋅1n1(1r1−1r2)
Where:
- f = focal length of the lens
- n1 = refractive index of the medium (air = 1)
- n2 = refractive index of the lens material (1.5)
- r1 and r2 are the radii of curvature of the lens.
Step 3: Determine the radii of curvature
Since the lens is biconvex and symmetric, we can assume:
- r1=r (the radius of the convex surface)
- r2=−r (the radius of the other convex surface, taken as negative)
Using the given focal length:
16.25=(1.5−1)⋅11(1r−1−r)
16.25=0.5⋅(2r)
16.25=1r
Thus, r=6.25 cm.
Step 4: Calculate the new focal length in water
Now, when the lens is cut, one piece has one flat surface (infinite radius of curvature) and the other surface with radius r=6.25 cm. The new focal length f′ when the lens is in water can be calculated using the modified Lens Maker's Formula:
1f′=(n2−n1)⋅1n1(1r1−1∞)
Where:
- n1=43 (refractive index of water)
- n2=1.5 (refractive index of the lens)
- r1=6.25 cm
Substituting the values:
1f′=(1.5−43)⋅143⋅16.25
Calculating 1.5−43=1.5⋅3−43=4.5−43=0.53:
1f′=(0.53)⋅(34)⋅16.25
1f′=0.54⋅6.25=0.525=150
Thus, f′=50 cm.
Step 5: Calculate the focal power in diopters
Focal power P in diopters is given by:
P=1f′ (in meters)
Converting f′ from cm to meters:
f′=0.50 m
Thus,
P=10.50=2 diopters
Final Answer
The focal power of the piece immersed in water is 2 diopters.
We have a biconvex lens with a focal length of 6.25 cm and a refractive index of 1.5. When cut into two pieces, one piece is placed in water (refractive index = 4/3). We need to find the focal power of the piece in water.
The Lens Maker's Formula is given by:
1f=(n2−n1)⋅1n1(1r1−1r2)
Where:
- f = focal length of the lens
- n1 = refractive index of the medium (air = 1)
- n2 = refractive index of the lens material (1.5)
- r1 and r2 are the radii of curvature of the lens.
Since the lens is biconvex and symmetric, we can assume:
- r1=r (the radius of the convex surface)
- r2=−r (the radius of the other convex surface, taken as negative)
16.25=(1.5−1)⋅11(1r−1−r)
16.25=0.5⋅(2r)
16.25=1r
Thus, r=6.25 cm.
Now, when the lens is cut, one piece has one flat surface (infinite radius of curvature) and the other surface with radius r=6.25 cm. The new focal length f′ when the lens is in water can be calculated using the modified Lens Maker's Formula:
1f′=(n2−n1)⋅1n1(1r1−1∞)
Where:
- n1=43 (refractive index of water)
- n2=1.5 (refractive index of the lens)
- r1=6.25 cm
1f′=(1.5−43)⋅143⋅16.25
Calculating 1.5−43=1.5⋅3−43=4.5−43=0.53:
1f′=(0.53)⋅(34)⋅16.25
1f′=0.54⋅6.25=0.525=150
Thus, f′=50 cm.
Focal power P in diopters is given by:
P=1f′ (in meters)
Converting f′ from cm to meters:
f′=0.50 m
Thus,
P=10.50=2 diopters
The focal power of the piece immersed in water is 2 diopters.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE -I (LEVEL-I(MAIN) STRAIGHT OBJECTIVE TYPE QUESTIONS)
21 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE -I (LEVEL-II LECTURE SHEET (ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS)
29 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - PRACTICE SHEET (EXERCISE III LEVEL -II (ADVANCED) LINKED COMPREHENSION TYPE QUESTIONS)
3 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
10 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - PRACTICE EXERCISE
106 Videos
Similar Questions
A plano-convex lens is made of refractive index of 1.6. The focal length of the lens is
View SolutionAn equiconvex lens of refractive index 1.6 has power 4D in air. Its power in water is:
View SolutionA convex lens of refractive index 1.5 has a focal length of 20 cm in air. Calculate the change in its focal length when it is immersed in water of refractive index 4/3.
View SolutionA thin equiconvex lens (μ=3/2) of focal length 10cm is cut and separated and a material of refractive index 3 is filled between them. What is the focal length of the combination?

View SolutionA converging lens has a focal length of 20cm in air. It is made of a material of refractive index 1.6. If it is immersed in a liquid of refractive index 1.3, what will be its new foacl length ?
View SolutionA thin lens made of a material of refractive index μ0 has a focal length f0 in air. Find the focal length of this lens if it is immersed in a liquid of refractive index μ.
View SolutionA concavo-convex lens is made of glass of refractive index 1.5. The radii of curvature of its two surfaces are 30cm and 50cm. Its focal length when placed in a liquid of refractive index 1.4 is
View SolutionA thin lens (μ=1.5) of focal length + 12 cm is immersed in water (μ=1.33). What is its new focal length ?
View SolutionA parallel beam of light falls successively on a thin convex lens of focal length 40 cm and then ono a thini convex lens of focal length 10cm as shown in figure.
In figure, the second lens is an equiconcave lens of focal length 10cm and made of a material of refractive index 1.5. In both the cases, the second lens has an aperture equal to 1cm.
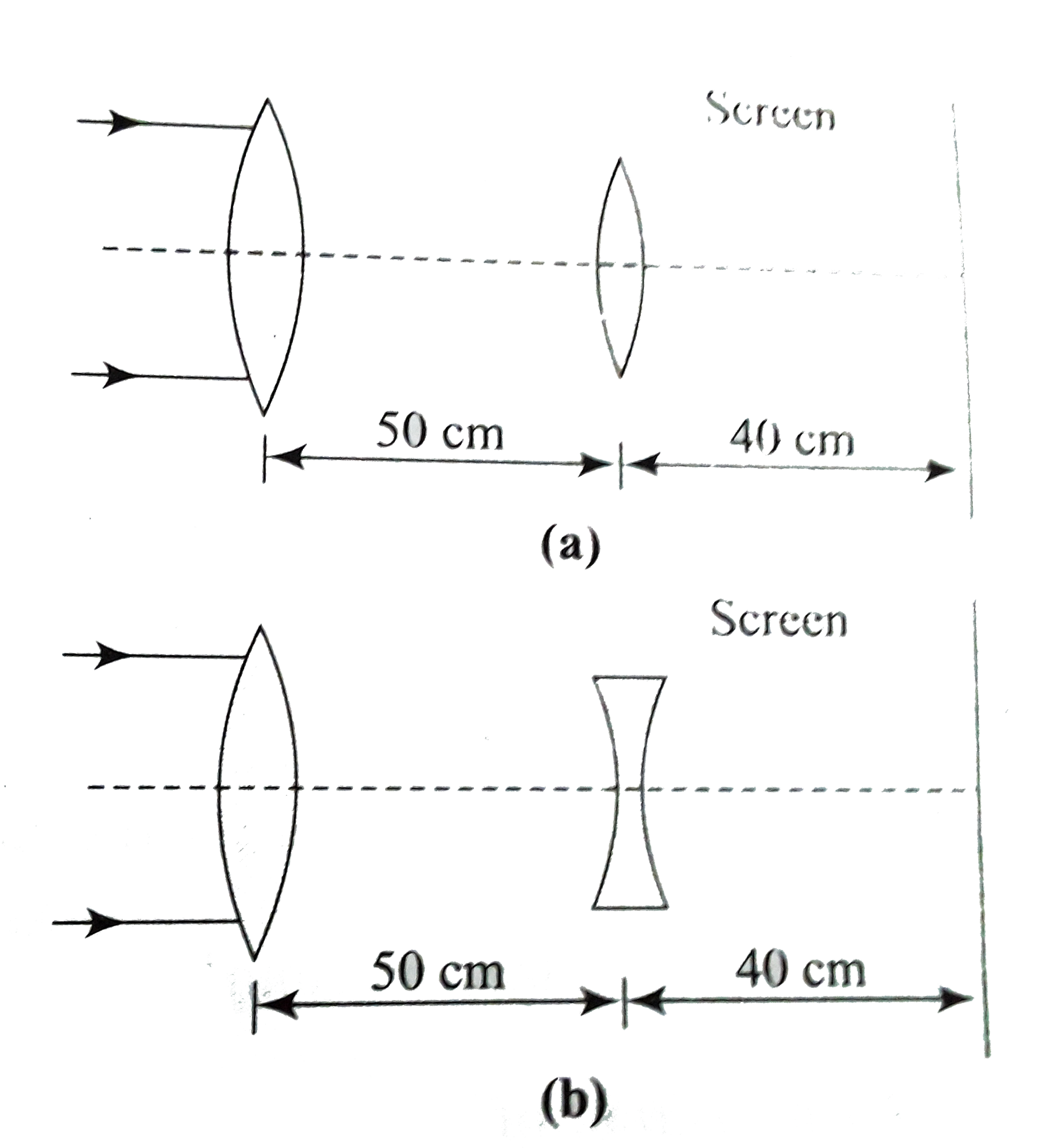
Q. Now, a liquid of refractive index μ is filled to the right of the second lens in case B such that the area illuminated in both the cases is the same. Determing the refractive index of the liquid.
View SolutionAn equi-convex lens of focal length F in air is is cut into two halves along the plane perpendicular to the optic axis. One of the halves is placed between a fixed object and a screen separated by distance of 90 cm . Two images are formed on the screen for two different positions of the lens with magnification 2 and 1/2 respectively. Find the value of F . what would be the value of the focal length of the equiconvex lens if the lens is immersed in water ? Refractive index of the material of the lens is 1.5 and that of water is μw=4/3.
View Solution
