A firm hires out 3 cars every day. The demand for a car on each day is distributed as a poisson distribution with mean 2.0. The probability that some demand is refused on a day is (e−2=0.135)
0.2177
0.1912
0.1455
0.0192
The correct Answer is:C
To solve the problem, we need to find the probability that some demand for cars is refused on a given day. This occurs when the demand exceeds the number of cars available for hire, which is 3 in this case. We can model the demand using a Poisson distribution with a mean (λ) of 2.0.
1. Define the Random Variable:
Let X be the number of cars hired per day. Since the demand follows a Poisson distribution with a mean of λ=2.0, we can express this as:
P(X=k)=e−λλkk!
2. Identify the Event of Interest:
We need to find the probability that some demand is refused. This happens when the demand X exceeds the number of cars available, which is 3. Therefore, we need to calculate:
P(X>3)=1−P(X≤3)
3. Calculate P(X≤3):
We can express P(X≤3) as:
P(X≤3)=P(X=0)+P(X=1)+P(X=2)+P(X=3)
Using the Poisson formula, we calculate each term:
- For k=0:
P(X=0)=e−2⋅200!=e−2⋅1=e−2
- For k=1:
P(X=1)=e−2⋅211!=e−2⋅2
- For k=2:
P(X=2)=e−2⋅222!=e−2⋅42=2e−2
- For k=3:
P(X=3)=e−2⋅233!=e−2⋅86=43e−2
4. Sum the Probabilities:
Now we sum these probabilities:
P(X≤3)=e−2+2e−2+2e−2+43e−2
Combine the terms:
P(X≤3)=e−2(1+2+2+43)=e−2(5+43)
Convert 5 to a fraction:
5=153⇒P(X≤3)=e−2(15+43)=e−2⋅193
5. Calculate P(X>3):
Now we can find P(X>3):
P(X>3)=1−P(X≤3)=1−e−2⋅193
6. Substitute the Value of e−2:
Given that e−2=0.135:
P(X>3)=1−0.135⋅193
Calculate 0.135⋅193:
=0.135⋅6.3333≈0.855
Therefore:
P(X>3)=1−0.855=0.145
Final Answer:
The probability that some demand is refused on a day is approximately 0.145.
Let X be the number of cars hired per day. Since the demand follows a Poisson distribution with a mean of λ=2.0, we can express this as:
P(X=k)=e−λλkk!
We need to find the probability that some demand is refused. This happens when the demand X exceeds the number of cars available, which is 3. Therefore, we need to calculate:
P(X>3)=1−P(X≤3)
We can express P(X≤3) as:
P(X≤3)=P(X=0)+P(X=1)+P(X=2)+P(X=3)
Using the Poisson formula, we calculate each term:
- For k=0:
P(X=0)=e−2⋅200!=e−2⋅1=e−2
- For k=1:
P(X=1)=e−2⋅211!=e−2⋅2
- For k=2:
P(X=2)=e−2⋅222!=e−2⋅42=2e−2
- For k=3:
P(X=3)=e−2⋅233!=e−2⋅86=43e−2
Now we sum these probabilities:
P(X≤3)=e−2+2e−2+2e−2+43e−2
Combine the terms:
P(X≤3)=e−2(1+2+2+43)=e−2(5+43)
Convert 5 to a fraction:
5=153⇒P(X≤3)=e−2(15+43)=e−2⋅193
Now we can find P(X>3):
P(X>3)=1−P(X≤3)=1−e−2⋅193
Given that e−2=0.135:
P(X>3)=1−0.135⋅193
Calculate 0.135⋅193:
=0.135⋅6.3333≈0.855
Therefore:
P(X>3)=1−0.855=0.145
The probability that some demand is refused on a day is approximately 0.145.
Similar Questions
If for a poisson distribution P(X=0)=0.2 then the variance of the distribution is
View SolutionIf the number of telephone calls an operator receives between 10:00 am to 10:10 pm follow poisson distribution with mean 3. The probability that the operator receives one call during that interval the next day is
View Solution
Knowledge Check
In a binomial distribute if probability of getting success is 14 and standard deviation is 32 then mean is
A1B3C9D12
In a city 10 accident take place in a span of 50 days. Assuming that the number of accidents follow the Poisson distribution, the probability that three or more accident occure in a day , is
View SolutionIn a Poisson distribution P(X=0) =2P(X=1) then the standard deviation =
View SolutionIn binomial probability distribution, mean is 3 and standard deviation is 32. Then the value of p is
View SolutionThe mean and variance of a random variable X having a binomial probability distribution are 6 and 3 respectively, then the probabiltiy P(X≥2) is
View SolutionDaya gets pocket money from his father every day. Out of the pocket money, he saves Rs 2.75 on first day, Rs 3.00 on second day, Rs 3.25 on third day and so on. Find:
the total amount saved by him in 30 days.
View SolutionIf it rains a dealer in rain coats can earn Rs . 500 Rs a day . If it is fair , he can loose Rs.40/- per day . His mean profit if the probability of a fair day is 0.6 is
View Solution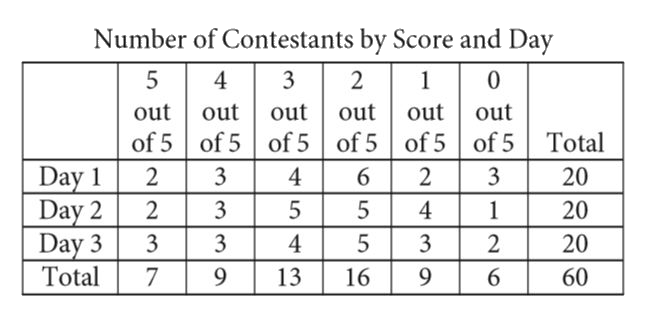
The same 20 contestants, on each of 3 days, answered 5 questions in order to win a prize. Each contestant received 1 point for each correct answer. The number of contestants receiving a given score on each day is shown in the table above.
No contestant received the same score on two different days. If a contestant is selected at random, what is the probability that the selected contestant received a score of 5 on Day 2 or Day 3, given that the contestant received a score of 5 on one of the three days?
View Solution
