A box of mass 4 Kg is placed on a rough inclined plane of inclination 60∘. Its downward motion can be prevented by applying an upward pull F. And it can be made to slide upwards by applying a force 3F. The coefficient of friction between the box and inclined plane is
2√3
√32
1√2
12
The correct Answer is:B
To solve the problem, we need to analyze the forces acting on the box on the inclined plane and set up equations based on the conditions given.
Step 1: Identify the forces acting on the box
The forces acting on the box are:
1. The weight of the box (mg) acting downward.
2. The normal force (N) acting perpendicular to the inclined plane.
3. The frictional force (f) acting opposite to the direction of motion.
Step 2: Resolve the weight into components
The weight can be resolved into two components:
- Parallel to the incline: mgsinθ
- Perpendicular to the incline: mgcosθ
Given:
- Mass m=4kg
- Inclination θ=60∘
- Gravitational acceleration g=9.8m/s2
Step 3: Write the equations for the two scenarios
1. Preventing downward motion:
The upward force F must balance the downward forces:
F=mgsinθ−μmgcosθ(1)
2. Sliding upwards:
The applied force 3F must overcome both the weight component and friction:
3F=mgsinθ+μmgcosθ(2)
Step 4: Substitute the values into the equations
Substituting m=4kg and g=9.8m/s2:
- mg=4×9.8=39.2N
- sin60∘=√32
- cos60∘=12
Now substituting these into equations (1) and (2):
1. From (1):
F=39.2⋅√32−μ⋅39.2⋅12
F=19.6√3−19.6μ
2. From (2):
3F=39.2⋅√32+μ⋅39.2⋅12
3F=19.6√3+19.6μ
Step 5: Relate the two equations
Now we can express F from both equations:
From (1):
F=19.6√3−19.6μ
From (2):
F=19.6√3+19.6μ3
Step 6: Set the two expressions for F equal to each other
19.6√3−19.6μ=19.6√3+19.6μ3
Step 7: Clear the fraction by multiplying through by 3
3(19.6√3−19.6μ)=19.6√3+19.6μ
58.8√3−58.8μ=19.6√3+19.6μ
Step 8: Rearranging the equation
58.8√3−19.6√3=58.8μ+19.6μ
39.2√3=78.4μ
Step 9: Solve for the coefficient of friction (μ)
μ=39.2√378.4=√32
Final Answer
The coefficient of friction μ between the box and the inclined plane is √32.
---
The forces acting on the box are:
1. The weight of the box (mg) acting downward.
2. The normal force (N) acting perpendicular to the inclined plane.
3. The frictional force (f) acting opposite to the direction of motion.
The weight can be resolved into two components:
- Parallel to the incline: mgsinθ
- Perpendicular to the incline: mgcosθ
- Mass m=4kg
- Inclination θ=60∘
- Gravitational acceleration g=9.8m/s2
1. Preventing downward motion:
The upward force F must balance the downward forces:
F=mgsinθ−μmgcosθ(1)
2. Sliding upwards:
The applied force 3F must overcome both the weight component and friction:
3F=mgsinθ+μmgcosθ(2)
Substituting m=4kg and g=9.8m/s2:
- mg=4×9.8=39.2N
- sin60∘=√32
- cos60∘=12
1. From (1):
F=39.2⋅√32−μ⋅39.2⋅12
F=19.6√3−19.6μ
3F=39.2⋅√32+μ⋅39.2⋅12
3F=19.6√3+19.6μ
Now we can express F from both equations:
From (1):
F=19.6√3−19.6μ
F=19.6√3+19.6μ3
19.6√3−19.6μ=19.6√3+19.6μ3
3(19.6√3−19.6μ)=19.6√3+19.6μ
58.8√3−58.8μ=19.6√3+19.6μ
58.8√3−19.6√3=58.8μ+19.6μ
39.2√3=78.4μ
μ=39.2√378.4=√32
The coefficient of friction μ between the box and the inclined plane is √32.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - MOTION IN A PLANE87videos
APPENDICES (REVISION EXERCISE)
- BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )52videos
APPENDICES ( REVISION EXERCISE )
- BOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - PRACTICE EXERCISE21videos
ATOMS
Similar Questions
A box of mass 8kg placed on a rough inclined plane of inclination θ its downward motion can be prevented by applying an upward pull F and it can be made to slide upward appliying a force 2F .The coefficient of friction between the box and the inclined plane is
View SolutionA box of mass 8kg placed on a rough inclined plane of inclened θ its downward motion can be prevented by applying an upward pull F and it can be made to slide upward appliying a force 2F .The coefficient of friction between the box and the inclined plane is
View SolutionA box of mass 8kg placed on a rough inclined plane of inclination θ its downward motion can be prevented by applying an upward pull F and it can be made to slide upward appliying a force 2F .The coefficient of friction between the box and the inclined plane is
View SolutionA block of mass 5 kg is placed on a rough inclined plane. The inclination of the plane is gradually increased till the block just begins to slide down. The inclination of the plane is than 3 in 5. The coefficient of friction between the block and the plane is (Take, g=10m/s2)
View SolutionA block of mass 5 kg is at rest on a rough inclined surface. If angle of inclination of plane is 60∘, then force applied by it on block is
View SolutionA block of mass 4 kg is pulled along a smooth inclined plane of inclination 30∘ with constant velocity 3 m/s as shown, power delivered by the force is
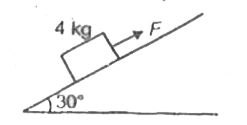 View Solution
View SolutionA block of mass 10 kg is placed on rough inclined plane of inclination angle 37∘ .Coefficient of friction between block & plane is 0⋅8, find minimum magnitude of F so that block remains at rest .
 View Solution
View SolutionA block of mass 10 kg is kept on a fixed rough (μ=0.8) inclined plane of angle of inclination 30∘. The frictional force acting on the block is
 View Solution
View SolutionAn object of mass 10kg is to be kept at rest on an inclined plane making an angle of 37∘to the horizontal by applying a force F along the plane upwards as shown in figure . The coefficient of static fiction between the object and the plane is 0.2 Find the magnitude of force F
[Take g=10ms−2]
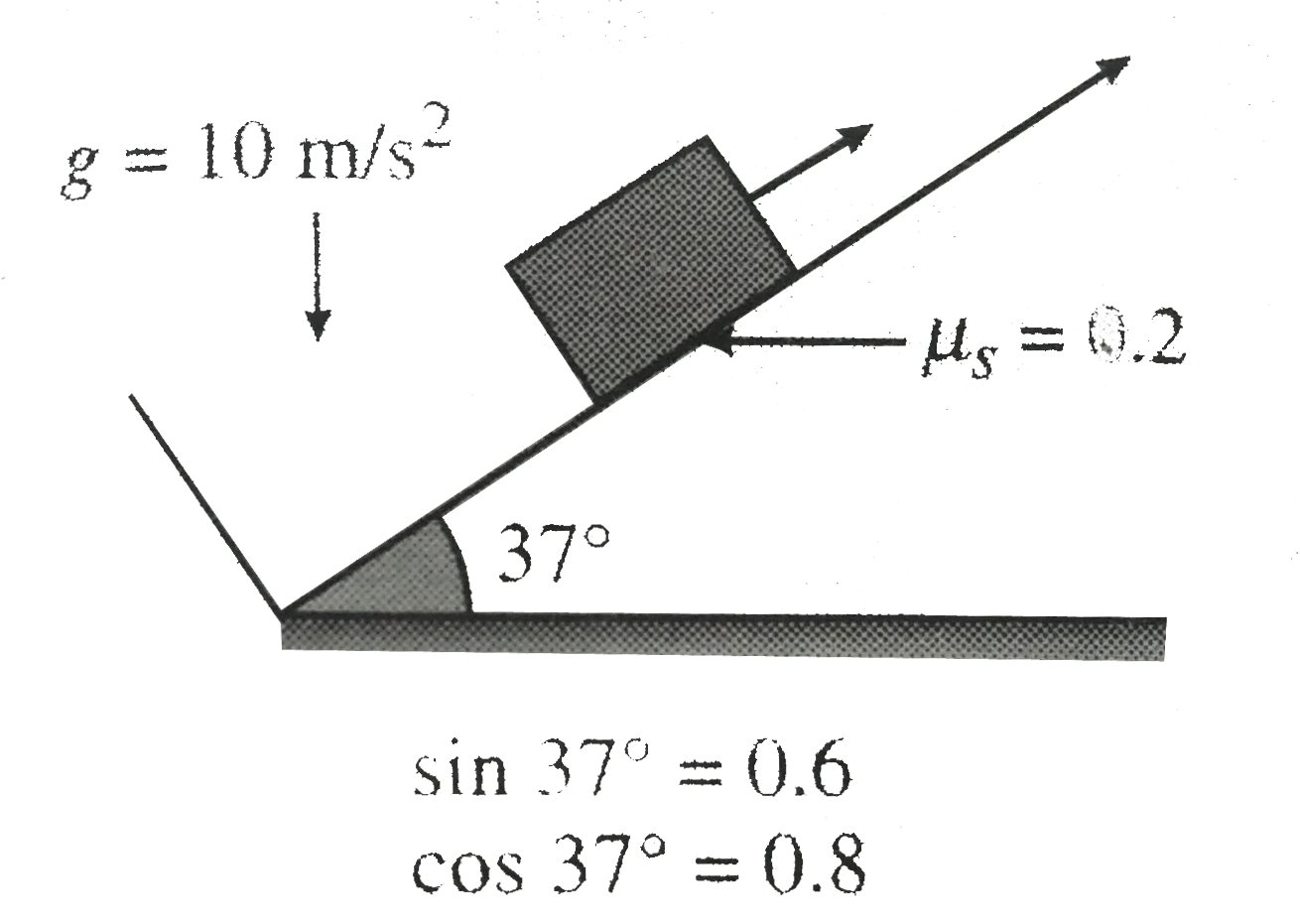 View Solution
View SolutionA block of mass m=3kg slides on a rough inclined plane of cofficient of friction 0.2 Find the resultant force offered by the plane on the block
 View Solution
View Solution

