A chain of 100 links is 1m long and has a mass of 2kg. With the ends fastened together it is set rotating at 3000 rpm, in a horizontal plane. The centripetal force on each link is
3.14N
31.4N
314N
3140N
The correct Answer is:C
To solve the problem of finding the centripetal force on each link of a chain rotating in a horizontal plane, we can follow these steps:
1. Identify the Given Data:
- Number of links, n=100
- Total length of the chain, L=1m
- Total mass of the chain, m=2kg
- Rotational speed, RPM=3000
2. Convert RPM to Revolutions per Second:
F=3000RPM60=50revolutions per second
3. Calculate the Radius of the Circle:
- The chain forms a circle when the ends are fastened together. The circumference of the circle is equal to the length of the chain.
L=2πr⟹r=L2π=12πm
4. Calculate Angular Velocity (ω):
ω=2πF=2π×50=100πrad/s
5. Calculate the Total Centripetal Force (F):
- The formula for centripetal force is given by:
F=mrω2
Substituting the values:
F=2×(12π)×(100π)2
Simplifying this:
F=2×12π×10000π2=10000N
6. Calculate the Centripetal Force on Each Link:
Centripetal force on each link=Fn=10000100=100N
Final Result:
The centripetal force on each link is 100 N.
- Number of links, n=100
- Total length of the chain, L=1m
- Total mass of the chain, m=2kg
- Rotational speed, RPM=3000
F=3000RPM60=50revolutions per second
- The chain forms a circle when the ends are fastened together. The circumference of the circle is equal to the length of the chain.
L=2πr⟹r=L2π=12πm
ω=2πF=2π×50=100πrad/s
- The formula for centripetal force is given by:
F=mrω2
Substituting the values:
F=2×(12π)×(100π)2
Simplifying this:
F=2×12π×10000π2=10000N
Centripetal force on each link=Fn=10000100=100N
The centripetal force on each link is 100 N.
Topper's Solved these Questions
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - MOTION IN A PLANE
87 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )
52 Videos
- ATOMSBOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - PRACTICE EXERCISE
21 Videos
Similar Questions
A chain of 125 links is 1.25 m long and has mass of 2 kg with the ends fastened together. It is set for rotating at 50 revolutions per second. The centripetal force on each link is
View SolutionThe thin rod shown below has mases M and length L. A force F acts at one end as shown and the rod is free to rotate about the other end in horizontal plane. Initial angular acceleration of the rod is :

View SolutionA body of mass 2 kg lying on a smooth surface is attached to a string 3 m long and then rotated in a horizontal circle making 60 rev/min. Calculate the centripetal acceleration.
View SolutionA stone of mass 100 g tied to the end of a string 80 cm long is whirled in a horizontal circle with a constant speed.If the stone makes 14 revolutions in 25 s, calculate the centripetal force acting on the stone.
View SolutionOne end of a string 0.5m long is fixed to a point A and the other end is fastened to a small object of weight 8N. The object is pulled aside by a horizontal force F, until it is0.3m from the vertical through A.Find the magnitude of the tension T in the string and force F.
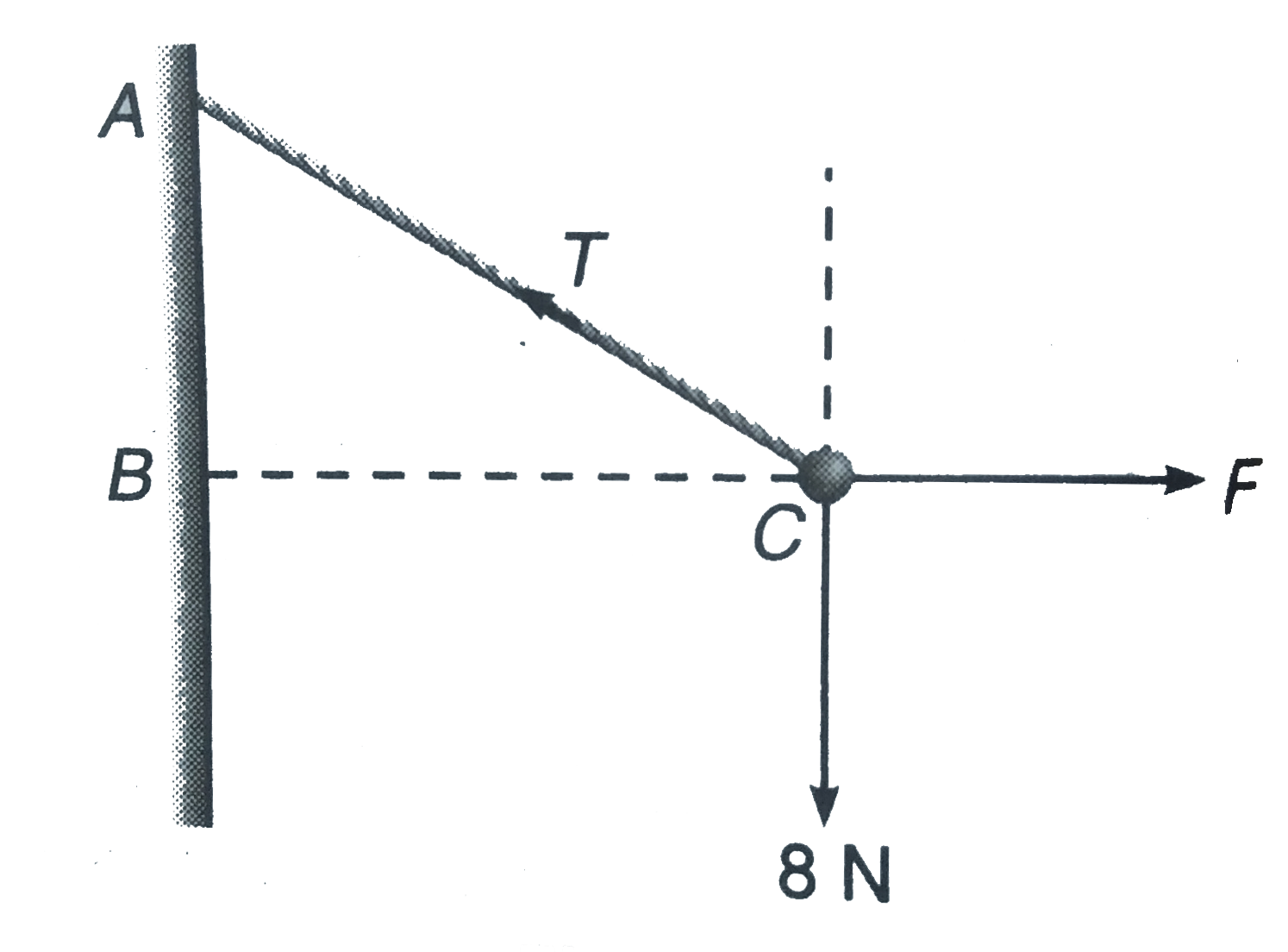
View SolutionOne end of a string 0.5m long is fixed to a point A and the other end is fastened to a small object of weight 8N. The object is pulled aside by a horizontal force F, until it is0.3m from the vertical through A.Find the magnitudes of the tension T in the string and force F.

View SolutionA metal bob of mass 0.6 kg is attached to the end of a string of length 1 m and the bob is whirled in a horizontal circle with a uniform speed of 12 m/s. What is the centripetal force acting on the bob ? If the speed of the bob is 5 m/s calculate the tension in the string.
View SolutionA string breaks under a load of 4.8kg A mass of 0.5 kg is attached to one end of a string 2 m long and is rotated in a horizontal circle . Calculate the greatest number of revolutions that the mass can make without breaking the string .
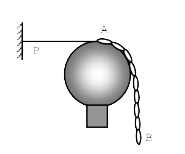
View SolutionA chain of mass per unit length λ and length 1.5 m rests on a fixed smooth sphere of radius R=2πm such that A end of chain is at the top of sphere while the other end is hanging freely. Chain is held stationary by a horizontal thread PA. The tension in the thread is:
View SolutionA particle of mass m and charge q is fastened to one end of a string of length. The other end of the string is fixed to the point O. The whole sytem liles on as frictionless horizontal plane. Initially, the mass is at rest at A. A uniform electric field in the direction shown in then switfched on. Then

View Solution
