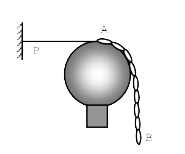
A chain of mass per unit length λ and length 1.5 m rests on a fixed smooth sphere of radius R=2πm such that A end of chain is at the top of sphere while the other end is hanging freely. Chain is held stationary by a horizontal thread PA. The tension in the thread is:
λg(12+2π)
λg(π2+2π)
λg(2π)
None of these
The correct Answer is:A
Length of the hanging part =(1.5−2πR4)=0.5m
∴T1=0.5λg
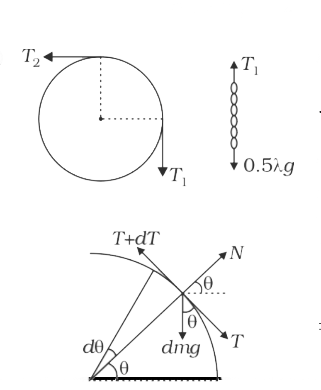
Consider the force diagram of a small mass dm=Rλdθ which subtends angle dθ at the centre and whose position vector with respect to the centre of the sphere makes an angle θ with horizontal.
⇒T+dT=T+(dm)gcosθ,N=(dm)gsinθ
⇒∫T2T1dT=Rλg∫π/20cosθ.dθ
⇒T2=T1+Rλg=0.5λg+2πλg=λg(12+2π)
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - LEVEL 2 ( NUMERICAL TYPE FOR JEE MAIN )16videos
DYNAMICS OF A PARTICLE
- BOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - JEE Main (Archive) Level - I29videos
DYNAMICS OF A PARTICLE
- BOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - LEVEL 175videos
DYNAMICS OF A PARTICLE
- BOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - JEE ADVANCED ARCHIVE68videos
DC CIRCUIT
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - IN-CHAPTER EXERCISE-G10videos
ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
Similar Questions
A unifrom flexible chain of length 32 m rests on a fixed smooth sphere of radius R=2π m such that one end A of chain is on the top of the sphere while the other end B is hanging freely. Chain is helpd stationary by a horizontal thread PA as shown . Calculate the acceleration of chain when the horizontal string PA is burnt ( g = 10 m/s2)
View SolutionA chain of length l and mass m lies on the surface of a smooth sphere of radius R>l with one end tied to the top of the sphere.
View SolutionA chain of length l and mass m lies of the surface of a smooth hemisphere of radius R>l with one end tied to the top of the hemisphere. Taking base of the hemisphere as reference line, find the gravitational potential energy of the chain.
 View Solution
View SolutionA chain of mass m and length L is held at rest on smooth horizontal surface such that a part I of the chain is hanging vertically from the table. If the chain is let go, what is its speed as its end just leaves the horizontal surface?
View SolutionA chain of length l is placed on a smooth spherical surface of radius R with one of its ends fixed at the top of the sphere. What will be the acceleration w of each element of the chain when its upper end is released? It is assumed that the length of the chain l<12πR.
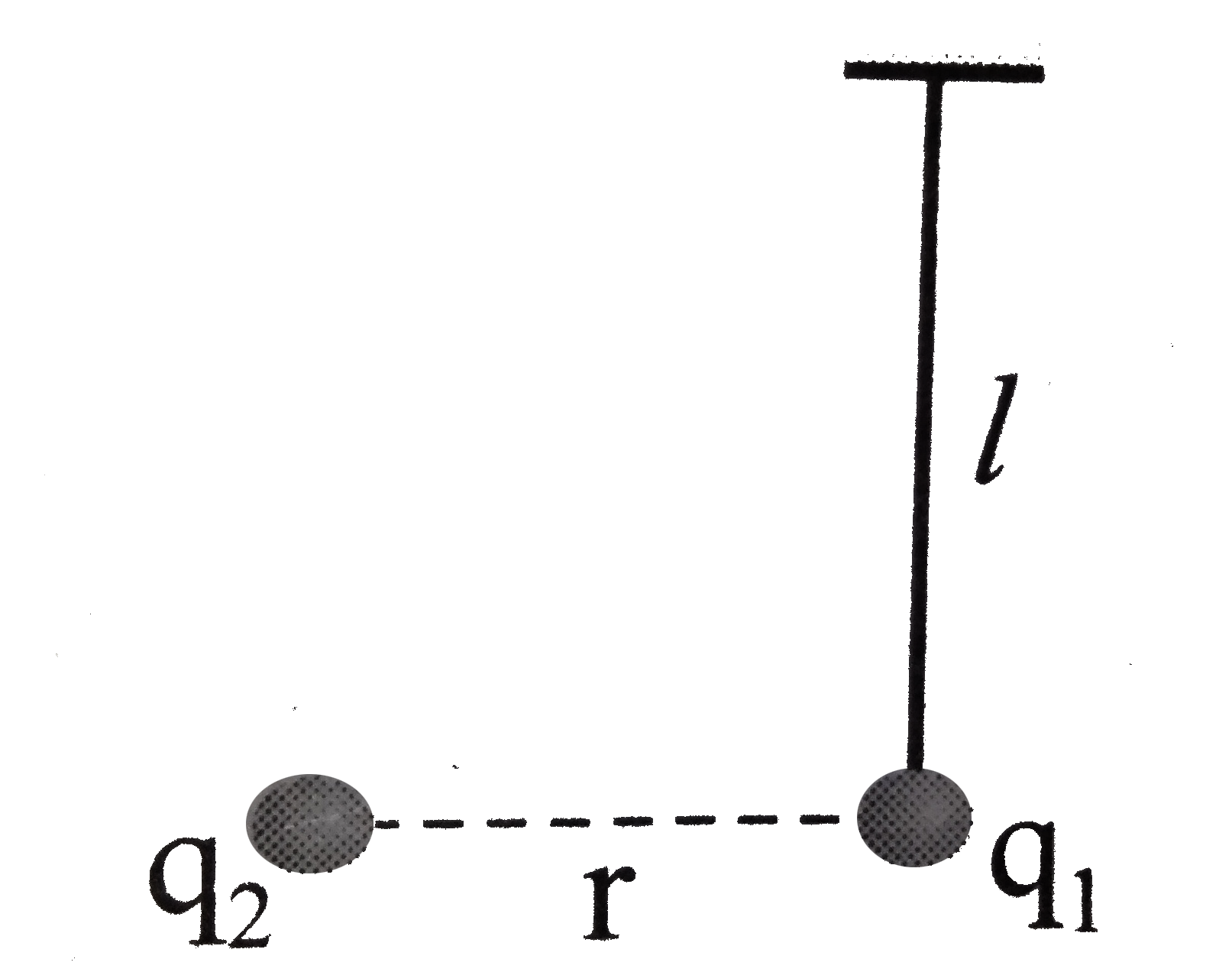
View SolutionAn isolated charge q1 of mass m is suspended freely by a thread of length l. Another charge q2 is brought near it (r>>l). When q1 is in equilibrium tension in thread will be
 View Solution
View SolutionA uniform chain of mass m & length L is kept on a smooth horizontal table such that Lnportion of the chaing hangs from the table. The work dione required to slowly bringsthe chain completely on the table is
View SolutionA block of mass M is resting on a smooth horizontal plane. One end of a uniform rope of mass M4 is fixed to the block , which pulled it in the horizontal direction by applying a force F at the other ends . The tension in the middle of the rope is
View SolutionA sphere of mass 20 g is whirled around in a horizontal circular path on the end of a string, the other end of which is stationary. If the tension in the string is 12.62 N, calculate the length of the string.
View SolutionA block of mass 1kg is tied to a string of length 1m the other end of which is fixed The block is moved on a smooth horizontal table with constant speed 10ms−1. Find the tension in the string
View Solution

