Give the magnitude and direction of the net force acting on .
a drop of rain falling down with a constant speed.
(b) a cork of mass 10 g floating on water.
(c ) a kite skillfully held stationary in the sky.
(d) high-speed electron in space far from all material objects. Give the direction electric and magnetic fields.
(a) As the rain drop is falling with a constant speed, its acceleration a = 0. Hence net force F = ma = 0.
(b) As the cork is floating on water, its weight is being balanced by the upthrust (equal to weight of water displaced). Hence net force on the cork is zero.
(c ) As the kite is held stationary, net force on the kite is zero, in accordance with Newton.s first law.
(d) Force is being applied to overcome the force of friction. But as velocity of the car is constant, its acceleration.
a = 0. Hence net force on the car F = ma = 0.
(e ) As no field (gravitational / electric / magnetic) is acting on the electron, net force on it is zero.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - Application6videos
LAWS OF MOTION
- BOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - I157videos
LAWS OF MOTION
- BOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWER5videos
LAWS OF MOTION
- BOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)10videos
GEOMETRICAL OPTICS
- BOOK - AAKASH SERIESCHAPTER - LOGIC GATESEXERCISE - Exercise (Very Short Answer)10videos
LOGIC GATES
Similar Questions
Give the magnitude and direction of the net force acting on
a Cork of mass 10 g floating on waterView SolutionGive the magnitude and direction of the net force acting on
(a) a drop of rain falling down with a constant speed
(b) a cork of mass 10 g floating on water
(c) a kite skillfully held stationary in the sky
(d) a car moving with a constant velocity of 30kh/h on a rough road
(e) a high speed electron in space free from all gravitational objects and free of electric and magnetic fields.View SolutionGive the magnitude and direction of the net force acting on
a kite skillfully held stationary in the skyView SolutionGive the magnitude and direction of the net force acting on
a high - speed electron in space far from all material objects, and free of electric and magnetic field .View SolutionGive the magnitude and direction of the force acting on a stone of mass 0.1 kg (a) just after it is dropped from the window of a stationary train
(b) just after it is dropped from the window of a train running at a constant velocity of 36km/hr
(c) just after it is dropped from the window of a train accelerating with 1ms−2
(d) lying on the floor of a train which is accelerating with 1ms−2 the stone being at rest relative to the train .
Neglect the resistance of air throughout .View SolutionA current i, indicated by the crosses in figure, is established in a strip of copper of height h and width w. A uniform field of magnetic induction B is applied at right angle to the strip.
(a) Calculate the drift velocity vd of the electrons.
(b) What are the magnitude and direction of the magnetic force F acting on the electrons?
(c) What should the magnitude and direction of a homogeneous electric field E be in order to counterbalance the effect of mangetic field?
(d) Calculate voltage V necessary between two sides of the conductor in order to creat this field E Between which sides of the conductor would this voltage have to be applied?
(e) If no electric field is applied from the outside, the electrons will be pushed somewhat to one side and therefore will give rise to a uniform electric field EH across the conductor until the forces of this electrostatic field EH balance the magnetic forces encountered in part (b). What will be the magnitude and direction of field EH?
Assume that n, the number of conductor electrons per unit volume is 1.1×1029m−3,h=0.02m,w=0.1cm,i=50A,andB=2T.
 View Solution
View SolutionA square shaped, conducting wire loop of side L, total mass m and total resistance R initially lies in the horizontal x−y plane, with corners at (x,y,z)=(0,0,0),(0,L,0),(L,0,0),and(L,L,0). There is a uniform upward magnetic field in the space within and around the loop. The side of the loop that extends from (0,0,0)→(L,0,0) is held in place on the x-axis, the rest of the loop is released, it begins to rotate due to the gravitational torque.
(a) Find the net torque (magnitude and direction)that acts on the loop when it has rotated through an anglr ϕ from its original orientation and is rotating dounward at an angular speed ω.
(b) Find the angular acceleration of the loop at the instant described in part (a).
( c) Compared to teh case with zero magnetic field, does it take the loop a longer or shorter time to rotate through 90∘ ? Explain.
(d) Is mechanical energy conserved as the loop rotates downward ? Explain.View SolutionA velocity filter uses the properties of electric and magnetic field to select particles that are moving with a specifice velocity. Charged particles with varying speeds are directed into the filter as shown. The filter consistt of an electric field E and a magnetic field B, each of constant magnitude, directed perpendicular to each other as shown, The charge particles will experience a force due to electric field given by F = qE. If positively charged particles are used, this force is towards right.
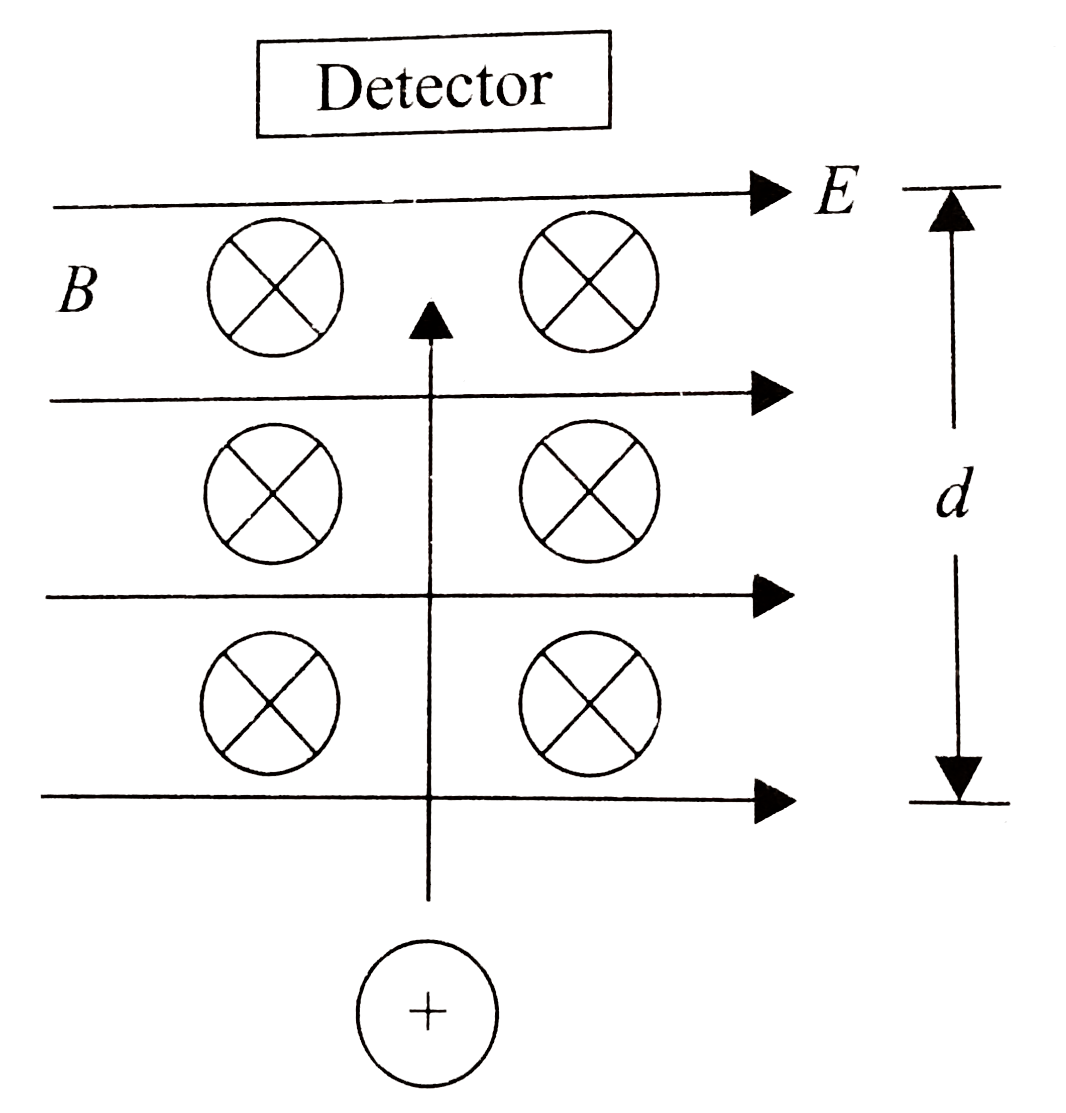
The moving particle will also experience a force due to magnetic field given by F=qvB. When forces due to the two fields are of equal magnitude, the net force on the particle will be zero, the particle will pass through centre with its path unaltered. The electric and magnetic fields can be adjusted t choose the specific velocity to be filtered. The efect of gravity can be neglected.
The electric and magnetic fields are adjusted to detect particles with positive charge q of certain speed v0. which of the following expressions is equal to this speed?View SolutionThe Betatron was the first important machine for producing high energy electrons. The action of the betatron depends on the same fundamental principle as that of the transformer in which an alternating current applied to a primary coil induces an altermating current usually with higher or lower voltage in the secondary coil. In the betatron secondary coil is replaced by a doughnut shaped vacuum chamber.Electron produced in the doughnut from a hot filament, are given a preliminary acceleration by the application of an electric field having potential difference of 20kV to 70kV, when an alternating magnetic field is applied parallel to the axis of the tube, two effects are produced (1) an electromotive force is produced in the electron orbit by the changing magnetic flux that gives an additional energy to the electrons (2) a radial force is produced by the action of magnetic field whose direction is perpendicular to the electron velocity. Which keeps the electron moving in a circular path. Conditions are arranged such that the increasing magnetic field keeps the electron in a circular orbit of constant radius. The mathematical relation between the betatron parameters to ensure the above condition is called BETATRON condition.
If the orbit radius of the circular path traced by the electron is R, magnetic field is B, speed of the electron is v, mass of the electron is m, charge on the electron is e and ϕ is the flux within the orbit of radius R. Then answer the following questions based on the above comprehension.
What is the tangential force acting on the electron ?View SolutionThe Betatron was the first important machine for producing high energy electrons. The action of the betatron depends on the same fundamental principle as that of the transformer in which an alternating current applied to a primary coil induces an altermating current usually with higher or lower voltage in the secondary coil. In the betatron secondary coil is replaced by a doughnut shaped vacuum chamber.Electron produced in the doughnut from a hot filament, are given a preliminary acceleration by the application of an electric field having potential difference of 20kV to 70kV, when an alternating magnetic field is applied parallel to the axis of the tube, two effects are produced (1) an electromotive force is produced in the electron orbit by the changing magnetic flux that gives an additional energy to the electrons (2) a radial force is produced by the action of magnetic field whose direction is perpendicular to the electron velocity. Which keeps the electron moving in a circular path. Conditions are arranged such that the increasing magnetic field keeps the electron in a circular orbit of constant radius. The mathematical relation between the betatron parameters to ensure the above condition is called BETATRON condition.
If the orbit radius of the circular path traced by the electron is R, magnetic field is B, speed of the electron is v, mass of the electron is m, charge on the electron is e and ϕ is the flux within the orbit of radius R. Then answer the following questions based on the above comprehension.
What is the value of d(m|→v|)dt ?View Solution

