A ball of √3×10−2kg hits a hard surface at 45∘ to normal with speed 4√2m/s and rebounds with 8/√3m/s, at 60∘ angle. If ball remains in contact for 0.1 sec, what force does it exert ?
To solve the problem step by step, we will follow these steps:
Step 1: Identify the given data
- Mass of the ball, m=√3×10−2kg
- Initial speed before hitting the surface, u=4√2m/s at an angle of 45∘ to the normal.
- Final speed after rebounding, v=8√3m/s at an angle of 60∘ to the normal.
- Time of contact, t=0.1s
Step 2: Resolve the initial velocity into components
The initial velocity u can be resolved into components along the normal direction (perpendicular to the surface):
un=u⋅cos(45∘)=4√2⋅1√2=4m/s
Step 3: Resolve the final velocity into components
The final velocity v can also be resolved into components along the normal direction:
vn=v⋅cos(60∘)=8√3⋅12=4√3m/s
Step 4: Calculate the change in velocity
The change in velocity Δv along the normal direction is given by:
Δv=vn−(−un)=4√3−(−4)=4√3+4
To combine these, we can express 4 in terms of a common denominator:
Δv=4+4√3√3m/s
Step 5: Calculate the change in momentum
The change in momentum Δp is given by:
Δp=m⋅Δv=√3×10−2⋅4+4√3√3=10−2⋅(4+4√3)kg m/s
Step 6: Calculate the force exerted
The force F exerted by the ball can be calculated using the formula:
F=Δpt=10−2⋅(4+4√3)0.1=10−1⋅(4+4√3)=0.4(1+√3)N
Final Answer
The force exerted by the ball is:
F=0.4(1+√3)N
---
- Mass of the ball, m=√3×10−2kg
- Initial speed before hitting the surface, u=4√2m/s at an angle of 45∘ to the normal.
- Final speed after rebounding, v=8√3m/s at an angle of 60∘ to the normal.
- Time of contact, t=0.1s
The initial velocity u can be resolved into components along the normal direction (perpendicular to the surface):
un=u⋅cos(45∘)=4√2⋅1√2=4m/s
The final velocity v can also be resolved into components along the normal direction:
vn=v⋅cos(60∘)=8√3⋅12=4√3m/s
The change in velocity Δv along the normal direction is given by:
Δv=vn−(−un)=4√3−(−4)=4√3+4
To combine these, we can express 4 in terms of a common denominator:
Δv=4+4√3√3m/s
The change in momentum Δp is given by:
Δp=m⋅Δv=√3×10−2⋅4+4√3√3=10−2⋅(4+4√3)kg m/s
The force F exerted by the ball can be calculated using the formula:
F=Δpt=10−2⋅(4+4√3)0.1=10−1⋅(4+4√3)=0.4(1+√3)N
The force exerted by the ball is:
F=0.4(1+√3)N
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - Application6videos
LAWS OF MOTION
- BOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - I157videos
LAWS OF MOTION
- BOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWER5videos
LAWS OF MOTION
- BOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)10videos
GEOMETRICAL OPTICS
- BOOK - AAKASH SERIESCHAPTER - LOGIC GATESEXERCISE - Exercise (Very Short Answer)10videos
LOGIC GATES
Similar Questions
A ball weighing 10g hits a hard surface vertically with a speed of 5m/s and rebounds with the same speed The ball remains in contact with the surface speed The ball remains in contact with the surface for 0.01s The average force exerted by the surface on the ball is .
View SolutionA body of mass 2kg collides with a wall with speed 100 m/s and rebounds with same speed. If the time of contact was 1/50 second, the force exerted on the wall is
View SolutionA 1 kg particle strikes a wall with velocity 1 m/s at an angle of 60o with the wall and reflects at the same angle. If it remains in contact with the wall for 0.1 s, then the force is
View SolutionA 3-kg steel ball strikes a wall with a speed of 10.0ms−1 at an angle of 60.0∘ with the surfaces of the wall. The ball bounces off with the same speed and same angle. If the ball was in contact with the wall for 0.2s, find the average force exerted by the wall on the ball.
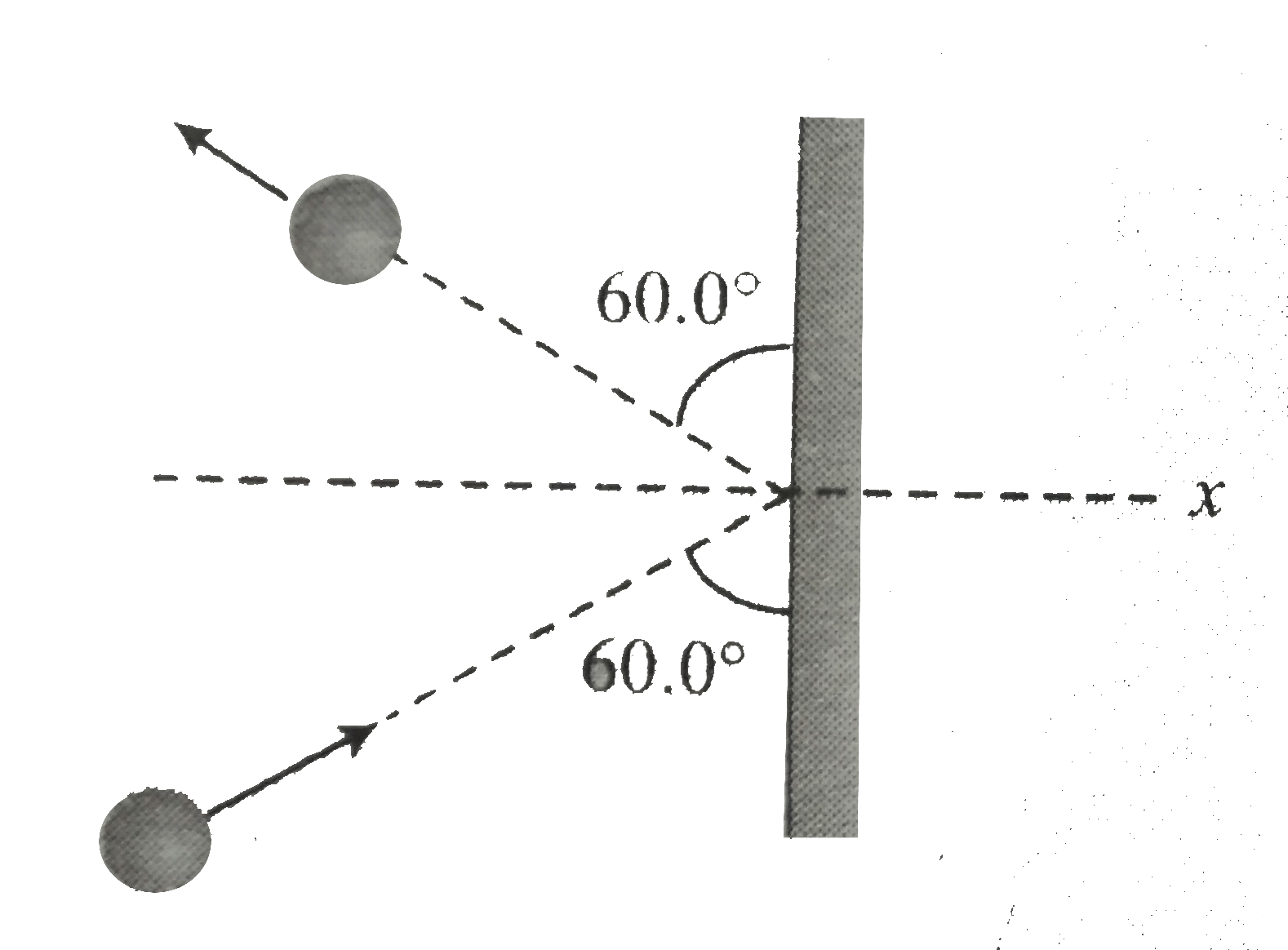 View Solution
View SolutionA 3.00kg steel hall strikes the wall with a speed of 10.0m/s at an angle of 60∘ with the surface. It bounces off with the same speed and angle. If the ball is in contact with the wall for 0.200s, what is the average force exerted by the wall on the ball?
View SolutionA spherical ball of mass 10−6 kg hits a wall 1000 times per second normally with a velocity of 1000 m/s and rebounds with same velocity along the initial direction. The force experienced by the wall is
View SolutionA ball of mass 3kg moving with a speed of 100 m/s, strikes a wall at an angle 60∘ (as shown in figure). The ball rebounds at the same speed and remains in contact with the wall for 0.2 s, the force exerted by the ball on the wall is
 View Solution
View SolutionA ball of mass 1kg drops vertically on to the floor wit a speed of 25m/s. It rebounds with an initial velocity of 10m/s. What impulse acts on the ball during contact ?
View SolutionA 0.5kg ball moving with a speed of 12m/s strikes a hard wall at an angle of 30∘ with the wall. It is reflected with the same speed and at the same angle . If the ball is in contact with the wall for 0.25s, the average force acting on the wall is
 View Solution
View SolutionA hockey player receives a corner shot at a speed of 15m/s at an angle of 30∘ with the y-axis and then shoots the ball along the x-axis with a speed of 30m/s If the mass of the ball is 150gm and it remains in contact with the hockey stick for 0.01s, the force imparted to the ball in the x-direction is :
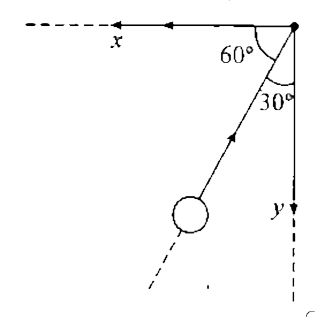 View Solution
View Solution

