Two blocks A and B of the same mass and surface finish are sliding on the same surface. Area of contact of A is twice that of the B. The frictional force between A and the surface is
twice that of B
half that of B
same that of B
depends on the power supplied
The correct Answer is:C
To solve the problem, we need to analyze the frictional forces acting on blocks A and B. Here’s a step-by-step solution:
Step 1: Understand the Given Information
- Both blocks A and B have the same mass (let's denote it as m).
- Both blocks are sliding on the same surface with the same surface finish, which implies they have the same coefficient of friction (μ).
- The area of contact of block A is twice that of block B.
Step 2: Calculate the Normal Force
The normal force (N) acting on each block can be calculated using the formula:
N=m⋅g
where g is the acceleration due to gravity.
Since both blocks have the same mass, the normal forces will be equal:
NA=NB=m⋅g
Step 3: Write the Frictional Force Formula
The frictional force (Ff) can be calculated using the formula:
Ff=μ⋅N
For block A:
FfA=μ⋅NA
For block B:
FfB=μ⋅NB
Step 4: Substitute the Normal Forces
Since NA=NB=m⋅g, we can write:
FfA=μ⋅(m⋅g)
FfB=μ⋅(m⋅g)
Step 5: Compare the Frictional Forces
Since both frictional forces depend on the same coefficient of friction and the same normal force, we can conclude:
FfA=FfB
Conclusion
The frictional force between block A and the surface is equal to the frictional force between block B and the surface. Thus, the frictional force between A and the surface is the same as that of B.
- Both blocks A and B have the same mass (let's denote it as m).
- Both blocks are sliding on the same surface with the same surface finish, which implies they have the same coefficient of friction (μ).
- The area of contact of block A is twice that of block B.
The normal force (N) acting on each block can be calculated using the formula:
N=m⋅g
where g is the acceleration due to gravity.
NA=NB=m⋅g
The frictional force (Ff) can be calculated using the formula:
Ff=μ⋅N
For block A:
FfA=μ⋅NA
For block B:
FfB=μ⋅NB
Since NA=NB=m⋅g, we can write:
FfA=μ⋅(m⋅g)
FfB=μ⋅(m⋅g)
Since both frictional forces depend on the same coefficient of friction and the same normal force, we can conclude:
FfA=FfB
The frictional force between block A and the surface is equal to the frictional force between block B and the surface. Thus, the frictional force between A and the surface is the same as that of B.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - II
136 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - PRACTICE EXERCISE
106 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - Application
6 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
10 Videos
- LOGIC GATESBOOK - AAKASH SERIESCHAPTER - LOGIC GATESEXERCISE - Exercise (Very Short Answer)
10 Videos
Similar Questions
Knowledge Check
The frictional force between two surfaces is independent of
ANature of the surfaceBSize of the bodyCArea of contactDMass of the bodyTwo blocks A and B of masses 10 kg and 15 kg are placed in contact with each other rest on a rough horizontal surface as shown in the figure. The coefficient of friction between the blocks and surface is 0.2. A horizontal force of 200 N is applied to block A. The acceleration of the system is (Take g=10ms−2)
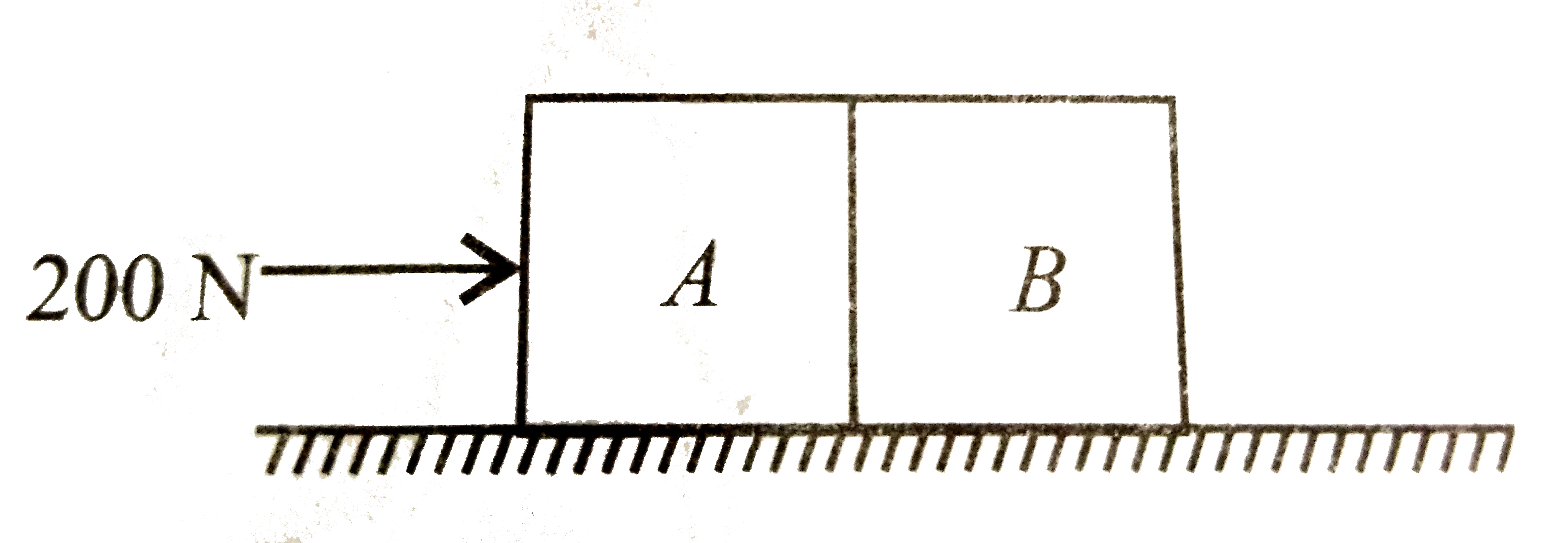 A4ms−2B6ms−2C8ms−2D10ms−2
A4ms−2B6ms−2C8ms−2D10ms−2
Choose the correct statement(s) about the frictional force between two solid surfaces in contact
View SolutionThe limiting value of static friction between two contact surfaces is
View SolutionThe limiting value of static friction between two contact surfaces is
View Solution(a) Find the acceleration of the two block shown in figuer (b) Find the friction force between alll contant surface

View SolutionIf we imagine two ideally smooth surfaces & if they are kept in contact, the frictional force acting between them is,
View SolutionTwo blocks A and B of masses 2kg and 3kg respectively, are placed on a horizontal surface as shown (one on top of other). Find the ratio of magnitude of normal reaction between A and B to that between B and the surface, respectively

View Solution
