A man of mass 62 kg is standing on a stationary boat of mass 238 kg. The man is carrying a sphere of mass 0.5 kg in his hands. If the man throws the sphere horizontally with a velocity of 12 ms−1, find the velocity with which the boat will move (in magnitude)
0.02ms−1
0.5ms−1
0.04ms−1
0.06ms−1
The correct Answer is:A
To solve the problem, we will use the principle of conservation of linear momentum. Here’s a step-by-step solution:
Step 1: Understand the System
We have a man, a boat, and a sphere. Initially, all are at rest, so the total initial momentum of the system is zero.
Step 2: Define the Variables
- Mass of the man (m₁) = 62 kg
- Mass of the boat (m₂) = 238 kg
- Mass of the sphere (m₃) = 0.5 kg
- Velocity of the sphere when thrown (v₃) = 12 m/s
- Velocity of the boat (v₂) = ? (to be determined)
Step 3: Apply Conservation of Momentum
According to the conservation of momentum:
Initial Momentum=Final Momentum
Initially, the momentum is:
Pi=0
After the man throws the sphere, the final momentum can be expressed as:
Pf=m₃⋅v₃+m₂⋅v₂+m₁⋅v₁
Since the man is not moving relative to the boat, we can assume that the velocity of the man (v₁) is equal to the velocity of the boat (v₂). Thus:
Pf=m₃⋅v₃+(m₂+m₁)⋅v₂
Step 4: Substitute the Values
Substituting the known values into the equation:
0=(0.5 kg⋅12 m/s)+(238 kg+62 kg)⋅v₂
Calculating the momentum of the sphere:
0=6 kg m/s+300 kg⋅v₂
Step 5: Solve for v₂
Rearranging the equation to solve for v₂:
300 kg⋅v₂=−6 kg m/s
v₂=−6 kg m/s300 kg
v₂=−0.02 m/s
Step 6: Determine the Magnitude
The magnitude of the velocity of the boat is:
|v₂|=0.02 m/s
Conclusion
The velocity with which the boat will move (in magnitude) is 0.02 m/s.
---
We have a man, a boat, and a sphere. Initially, all are at rest, so the total initial momentum of the system is zero.
- Mass of the man (m₁) = 62 kg
- Mass of the boat (m₂) = 238 kg
- Mass of the sphere (m₃) = 0.5 kg
- Velocity of the sphere when thrown (v₃) = 12 m/s
- Velocity of the boat (v₂) = ? (to be determined)
According to the conservation of momentum:
Initial Momentum=Final Momentum
Pi=0
Pf=m₃⋅v₃+m₂⋅v₂+m₁⋅v₁
Pf=m₃⋅v₃+(m₂+m₁)⋅v₂
Substituting the known values into the equation:
0=(0.5 kg⋅12 m/s)+(238 kg+62 kg)⋅v₂
0=6 kg m/s+300 kg⋅v₂
Rearranging the equation to solve for v₂:
300 kg⋅v₂=−6 kg m/s
v₂=−6 kg m/s300 kg
v₂=−0.02 m/s
The magnitude of the velocity of the boat is:
|v₂|=0.02 m/s
The velocity with which the boat will move (in magnitude) is 0.02 m/s.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - II
136 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
10 Videos
- LOGIC GATESBOOK - AAKASH SERIESCHAPTER - LOGIC GATESEXERCISE - Exercise (Very Short Answer)
10 Videos
Similar Questions
A man of mass m=2kg is standing on a platform of mass M=5kg, then at any instant.
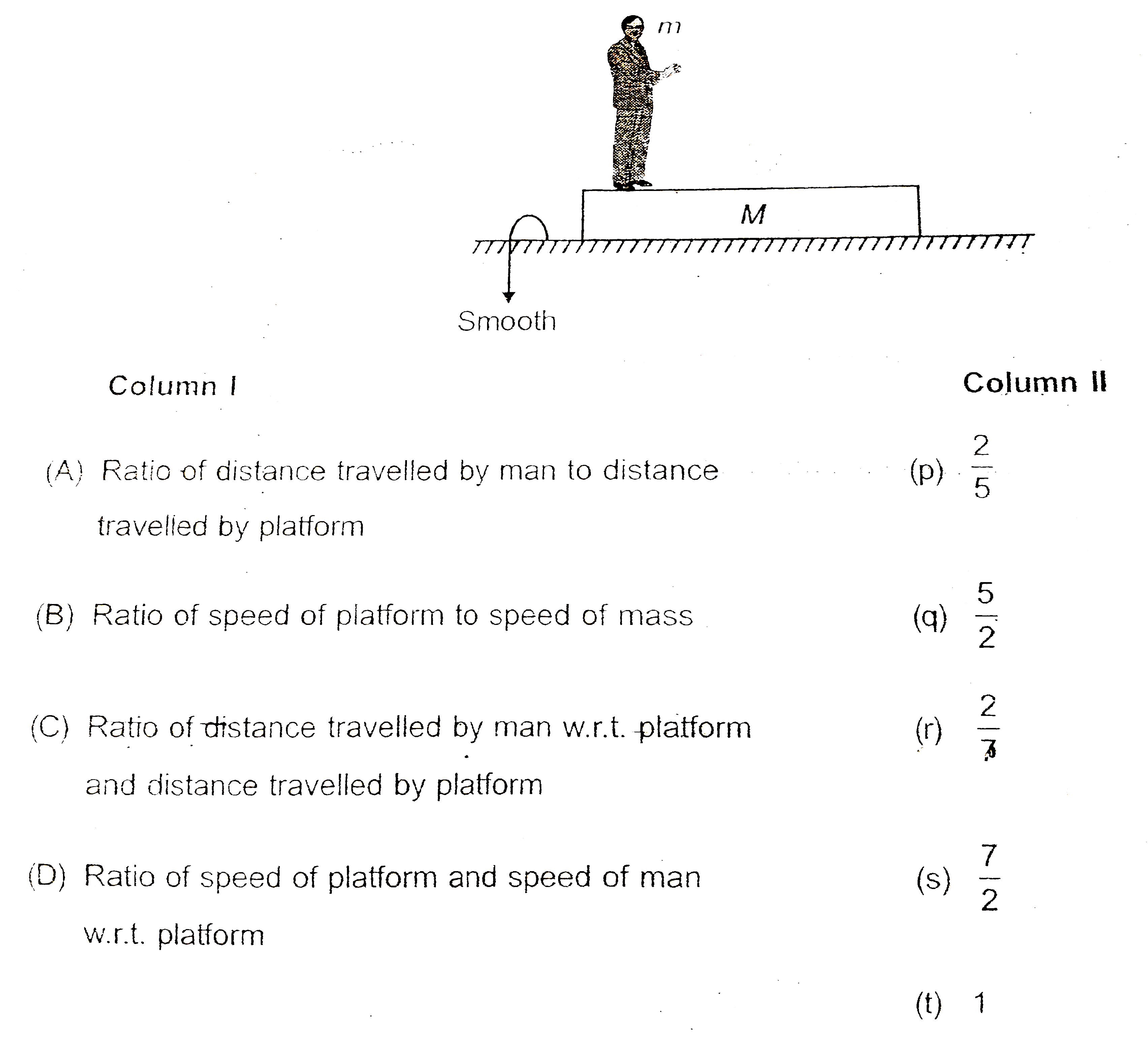
View SolutionA boy of mass 30 kg is standing at one end on a stationary boat over a lake. The boat has a mass 70 kg and length 10 m. Now the boy walked to the other end of the boat. Relative to the ground
View SolutionA man of mass m is standing on a stationary flat car of mass M. The car can move without friction along horizontal rails. The man starts walking with velocity v relative to the car. Work done by him
View SolutionA man of mass 60 kg is standing on a weighing machine kept in a box of mass 30 kg as shown in the diagram, If the man manages to keep the box stationary find the reading of the weighing machine.
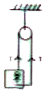
View SolutionA boat of mass 90 kg is floating in still water. A boy of mass 30 kg walks from one end to the other on it. If the length of the boat is 3 m, then the distance through which the boat will move is
View SolutionA man of 50kg is standing at one end on a boat of length 25m and mass 200kg.If he starts running and when he reaches the other end, has a velocity 2ms−1 with respect to the boat.The final velocity of the boat is
View SolutionA man of 50kg is standing at one end on a boat of length 25m and mass 200kg.If he starts running and when he reaches the other end, has a velocity 2ms−1 with respect to the boat.The final velocity of the boat is
View SolutionA man of mass 70 kg is standing at one end of a stationary, floating barge of mass 210 kg. he then walks to the other end of the barge, a distance of 90 meters. Ignore any frictional effect between the barge and the water.
Q. If the man walks at an average velocity of 8m/s what is the average velocity of the barge?
View SolutionA bomb of mass 12 kg explodes into two pieces of masses 4 kg and 8 kg. The velocity of mass 4 kg is 20 m/s. Find the velocity of mass 8 kg.
View SolutionA bomb of mass 12 kg explodes into two piece of masess 4 kg and 8kg . The velocity of mass 4 kg is 20 m/s . Find the velocity of mass 8 kg
View Solution
