A constant force actson a body of mass m, at rest and produces a velocity 'v' over a displacement 's1'. The same force acts on another body of mass m2 at rest and produces the same velocity. 'v' over a displacement 's2'. The ratio of the displacements is
m1:m2
m2:m1
√m1:√m2
√m2:√m1
The correct Answer is:A
To solve the problem, we need to analyze the motion of two bodies under the influence of the same constant force. Here's the step-by-step solution:
Step 1: Understand the given information
We have two bodies:
- Body 1 with mass m1=m (mass of the first body)
- Body 2 with mass m2
Both bodies start from rest and reach the same final velocity v over different displacements s1 and s2 respectively.
Step 2: Apply the third equation of motion
The third equation of motion relates initial velocity, final velocity, acceleration, and displacement:
v2=u2+2as
Since both bodies start from rest, the initial velocity u=0. Thus, the equation simplifies to:
v2=2as
Where a is the acceleration and s is the displacement.
Step 3: Express acceleration in terms of force and mass
From Newton's second law, we know that:
F=ma
Thus, the acceleration a can be expressed as:
a=Fm
Step 4: Substitute acceleration into the equation
Substituting a into the equation v2=2as:
v2=2(Fm)s
Rearranging gives:
s=mv22F
Step 5: Write the equations for both bodies
For body 1 (mass m1=m):
s1=mv22F
For body 2 (mass m2):
s2=m2v22F
Step 6: Find the ratio of displacements
Now we can find the ratio of the displacements s1s2:
s1s2=mv22Fm2v22F=mm2
Thus, the ratio of the displacements is:
s1s2=mm2
Final Answer
The ratio of the displacements s1 and s2 is mm2.
---
We have two bodies:
- Body 1 with mass m1=m (mass of the first body)
- Body 2 with mass m2
The third equation of motion relates initial velocity, final velocity, acceleration, and displacement:
v2=u2+2as
Since both bodies start from rest, the initial velocity u=0. Thus, the equation simplifies to:
v2=2as
Where a is the acceleration and s is the displacement.
From Newton's second law, we know that:
F=ma
Thus, the acceleration a can be expressed as:
a=Fm
Substituting a into the equation v2=2as:
v2=2(Fm)s
Rearranging gives:
s=mv22F
For body 1 (mass m1=m):
s1=mv22F
s2=m2v22F
Now we can find the ratio of the displacements s1s2:
s1s2=mv22Fm2v22F=mm2
s1s2=mm2
The ratio of the displacements s1 and s2 is mm2.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - II
136 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
10 Videos
- LOGIC GATESBOOK - AAKASH SERIESCHAPTER - LOGIC GATESEXERCISE - Exercise (Very Short Answer)
10 Videos
Similar Questions
Knowledge Check
A force of 6 N acts on a body at rest and mass 1 kg. During this time, the body attains a velocity of 30 m/s. The time for which the force acts on the body is
A10 secB8 secC7 secD5 sec
A constant force acts on a mass m at rest. Velocity acquired in travelling a fixed distance is directly proportional to :
View SolutionTwo bodies of masses 1 kg and 2 kg moving with same velocities are stopped by the same force. Then, the ratio of their stopping distances is
View SolutionA force of 10 N acts on a body of mass 2 kg for 3s , initially at rest. Calculate the velocity acquired by the body
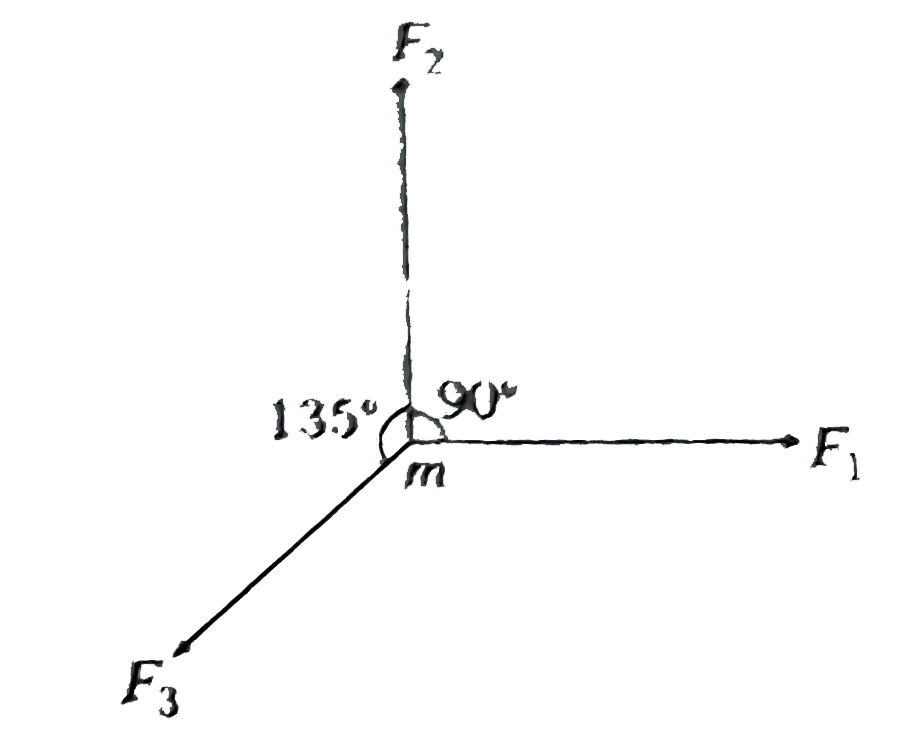
View SolutionWhen a force F acts on a body of mass m the acceleration product in the body is a . If three equal forces F1=F2=F3=F act on the same body as shown in figure the acceleration produced is
View SolutionA particle of mass 1 kg has a velocity of 2m/s. A constant force of 2N acts on the particle for 1s in a direction perpendicular to its initial velocity. Find the velocity and displacement of the particle at the end of 1 s.
View SolutionWhen a force F acs on a body of mass m the acceleration product in the body is a . If htree equal forces F1=F2=F3=F act on the same body as shown in figure the accleration produced is

View SolutionA body of mass m1 collides elastically with another body of mass m2 at rest. If the velocity of m1 after collision is 23 times its initial velocity, the ratio of their masses is :
View Solution
