If the centripetal force acting on a body revolving along a circular path of radius 25 m is 200 N, its KE is
A) 2.5 KJ
B) 4 KJ
C) 4.8 KJ
D) 6 J
The correct Answer is:A
To solve the problem, we need to find the kinetic energy (KE) of a body that is revolving in a circular path with a given centripetal force and radius. Here are the steps to find the solution:
Step 1: Understand the relationship between centripetal force, mass, and velocity.
The centripetal force (F) acting on a body moving in a circular path is given by the formula:
F=mv2r
where:
- F is the centripetal force,
- m is the mass of the body,
- v is the velocity of the body,
- r is the radius of the circular path.
Step 2: Substitute the known values into the formula.
From the problem, we have:
- F=200N
- r=25m
Substituting these values into the centripetal force formula:
200=mv225
Step 3: Rearrange the equation to find mv2.
Multiplying both sides by 25 gives:
mv2=200×25
mv2=5000kg m2/s2
Step 4: Use the kinetic energy formula.
The kinetic energy (KE) of the body is given by:
KE=12mv2
Step 5: Substitute mv2 into the kinetic energy formula.
Now substituting mv2=5000:
KE=12×5000
KE=2500J
Step 6: Convert Joules to kilojoules.
Since 1kJ=1000J:
KE=2.5kJ
Final Answer:
The kinetic energy of the body is 2.5kJ.
---
The centripetal force (F) acting on a body moving in a circular path is given by the formula:
F=mv2r
where:
- F is the centripetal force,
- m is the mass of the body,
- v is the velocity of the body,
- r is the radius of the circular path.
From the problem, we have:
- F=200N
- r=25m
200=mv225
Multiplying both sides by 25 gives:
mv2=200×25
mv2=5000kg m2/s2
The kinetic energy (KE) of the body is given by:
KE=12mv2
Now substituting mv2=5000:
KE=12×5000
KE=2500J
Since 1kJ=1000J:
KE=2.5kJ
The kinetic energy of the body is 2.5kJ.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - II
136 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
10 Videos
- LOGIC GATESBOOK - AAKASH SERIESCHAPTER - LOGIC GATESEXERCISE - Exercise (Very Short Answer)
10 Videos
Similar Questions
A tangential force of F = 1.5 N acts on a particle of mass m = 2 kg revolving in a circular path of radius r = 3 m. What is the work done by the torque for a complete revolution of the particle ?
View SolutionCentripetal acceleration of a cyclist completing 7 rounds in a minute along a circular track of radius 5 m with a constant speed ,is
View Solution
Knowledge Check
When a body moves in a circular path, outward force is called a ......
APseudo forceBCentrifugal forceCCentripetal forceDReaction force
A positive charge .Q. is fixed at a point, A negatively charged of mass .m. and charge .q. is revolving in a circular path of radius radius r1 with .Q. as the centre. The change in potential energy to change the radius of the circular path from r1andr2 in joule is
View SolutionA particle of mass 2 kg is moving along a circular path of radius 1 m. If its angular speed is 2π rad s−1, the centripetal force on it is
View SolutionTo move a body along a circular path the direction of centripetal force will be
View SolutionA particle of mass m is tied to light string and rotated with a speed v along a circular path of radius r. If T=tension in the string and mg= gravitational force on the particle then actual forces acting on the particle are
View SolutionA car of maas M is moving on a horizontal circular path of radius r. At an instant its speed is v and is increasing at a rate a.
View SolutionThe variation of force F acting on a body moving along x - axis varies with its position (x) as shown in figure
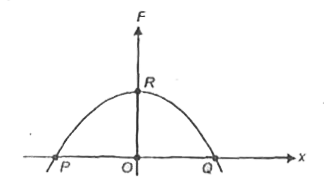
The body is in stable equilibrium stable at
View SolutionTwo point masses M are kept fixed on the x-axis at a distance a from the origin, another point mass m is moving in a circular path of radius R (in y - z plane) under the influence of gravitational force of attraction, then speed of m will be (Assume no forces are acting on m other than the gravitational forces by two M)
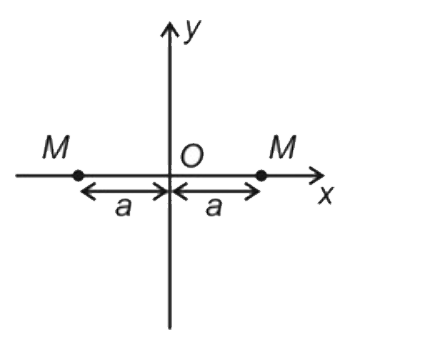
View Solution
