A bob is suspended from an ideal string of length 'l'. Now it is pulled to a side through 60∘ to vertical and whirled along a horizontal circle. Then its period of revolution is
A) π√lg
B) π√l2g
C) π√2lg
D) 2π√lg
The correct Answer is:C
To solve the problem, we need to find the period of revolution of a bob that is suspended from a string and is whirled in a horizontal circle at an angle of 60∘ to the vertical.
1. Identify the Forces Acting on the Bob:
- The forces acting on the bob are:
- Tension T in the string, acting along the string.
- Weight mg acting downward.
- Centrifugal force Fc acting horizontally due to circular motion.
2. Resolve the Tension into Components:
- The tension T can be resolved into two components:
- Vertical component: Tcosθ
- Horizontal component: Tsinθ
- Here, θ=60∘.
3. Set Up the Vertical Force Equation:
- In the vertical direction, the forces must balance:
Tcosθ=mg
- Substituting θ=60∘:
Tcos60∘=mg
- Since cos60∘=12:
T⋅12=mg⟹T=2mg
4. Set Up the Horizontal Force Equation:
- In the horizontal direction, the tension's horizontal component provides the necessary centripetal force:
Tsinθ=mω2r
- The radius r of the circular path can be expressed in terms of the length of the string L:
r=Lsinθ
- Substituting θ=60∘:
r=Lsin60∘=L⋅√32
- Now substituting r back into the horizontal force equation:
Tsin60∘=mω2(L⋅√32)
5. Substituting the Value of Tension:
- We already found T=2mg:
2mg⋅√32=mω2(L⋅√32)
- Simplifying gives:
mg√3=mω2(L⋅√32)
- Cancel m and √3 from both sides:
g=ω2L2
6. Solving for Angular Velocity ω:
- Rearranging gives:
ω2=2gL⟹ω=√2gL
7. Finding the Period of Revolution T:
- The period T is related to angular velocity by:
T=2πω
- Substituting ω:
T=2π√2gL=2π⋅√L2g=π√2Lg
Final Answer:
The period of revolution is:
T=π√2Lg
- The forces acting on the bob are:
- Tension T in the string, acting along the string.
- Weight mg acting downward.
- Centrifugal force Fc acting horizontally due to circular motion.
- The tension T can be resolved into two components:
- Vertical component: Tcosθ
- Horizontal component: Tsinθ
- Here, θ=60∘.
- In the vertical direction, the forces must balance:
Tcosθ=mg
- Substituting θ=60∘:
Tcos60∘=mg
- Since cos60∘=12:
T⋅12=mg⟹T=2mg
- In the horizontal direction, the tension's horizontal component provides the necessary centripetal force:
Tsinθ=mω2r
- The radius r of the circular path can be expressed in terms of the length of the string L:
r=Lsinθ
- Substituting θ=60∘:
r=Lsin60∘=L⋅√32
- Now substituting r back into the horizontal force equation:
Tsin60∘=mω2(L⋅√32)
- We already found T=2mg:
2mg⋅√32=mω2(L⋅√32)
- Simplifying gives:
mg√3=mω2(L⋅√32)
- Cancel m and √3 from both sides:
g=ω2L2
- Rearranging gives:
ω2=2gL⟹ω=√2gL
- The period T is related to angular velocity by:
T=2πω
- Substituting ω:
T=2π√2gL=2π⋅√L2g=π√2Lg
The period of revolution is:
T=π√2Lg
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - II
136 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
10 Videos
- LOGIC GATESBOOK - AAKASH SERIESCHAPTER - LOGIC GATESEXERCISE - Exercise (Very Short Answer)
10 Videos
Similar Questions
A bob of mass m attached to an inextensible string of length I is suspended from a vertical support. The bob rotates in a horizontal circle with an angular speed ω red/s about the vertical. About the point of suspension:
View SolutionA bob of mass 1 kg is suspended from an inextensible string of length 1 m. When the string makes an angle 60∘ with vertical, speed of the bob is 4 m/s
Net acceleration of the bob at this instant is
View SolutionA bob of mass 1 kg is suspended from an inextensible string of length 1 m. When the string makes an angle 60∘ with vertical, speed of the bob is 4 m/s
Upto what maximum height will the bob rise with respect to the bottommost point ?
View Solution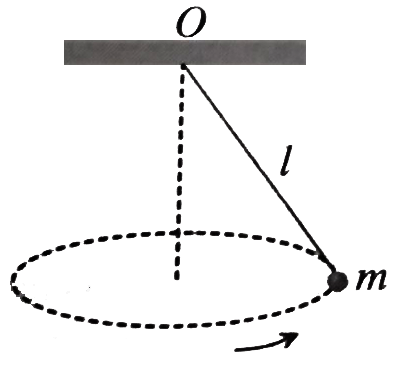
A point mass m is suspended from a light thread of length l, fixed at O, is whirled in a horizontal circle at constant speed as shown. From your point of view, stationary with respect to the mass, the forces on the mass are
View Solution
A point mass m is suspended from a light thread of length l, fixed at O, is whirled in a horizontal circle at constant speed as shown. From your point of view, stationary with respect to the mass, the forces on the mass are
View SolutionA force of 4N is inclined at an angle of 60∘ from the vertical. Find out its components along horizontal and vertical directions.

View SolutionA force of 4N is inclined at an angle of 60∘ from the vertical. Find out its components along horizontal and vertical directions.

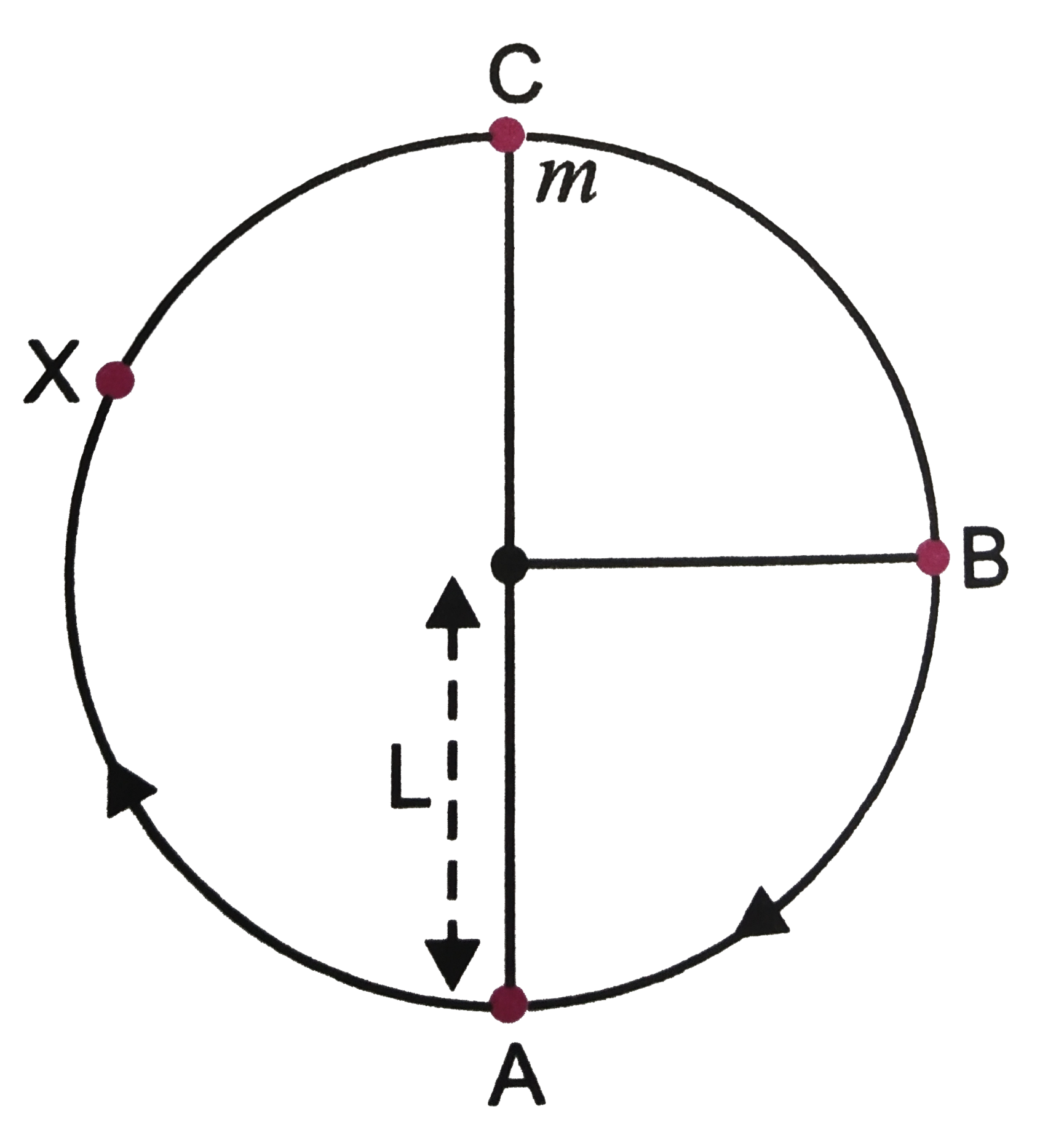
View SolutionA bob of mass m suspended by a light string of length L is whirled into a vertical circle as shown in figure . What will be the trajectory of the particle if the string is cut at
(a) Point B ? (b) Point C? (c) Point X?
View SolutionA bob hangs from a rigid support by an inextensible string of length l. It is released from rest when string makes an agngle 60∘ with vertical . The speed of the bob at the lowest position is
View SolutionA particle of mass m is suspended from a ceiling through a string of length L. The particle moves in a horizontal circle of radius r. Find a. the speed of the particle and b. the tension in the string. Such a system is called a conical pendulum.
View Solution
