A particle is at x=+5 m at t=0,
x=-7m at t=6 s and x =+2 at t=10s.Find the averahe velocity of the particle during the intervals
(a)t=0 to t=6s
(b)t=6s to t=10s,
(c)t=0 to t=10 s.
The correct Answer is:1
From the defination of averahe velocity
v=ΔxΔt=x2−x1t2−t1
(a)The average velocity between the times
t=0 t=6s
x1=+5,t1=0x2=−7mt2=6s
Hence v1=x1−x1t2−t1=−7−56−0=−2ms−1
(b) The average velocity between the times
t2=6s to t3=10s is
v2=x3−x2t3−t2=2−(−7)10−6=94=2.25ms−1
(c )The average velocity betwee times
t1=0 to t3=10s is
v3=x3−x1t3−t1=2−510−0=0.3ms−1
Similar Questions
A particle moves rectilinearly possessing a parabolic s-t graph. Find the average velocity of the particle over a time interval from t=12s→t=1.5s.
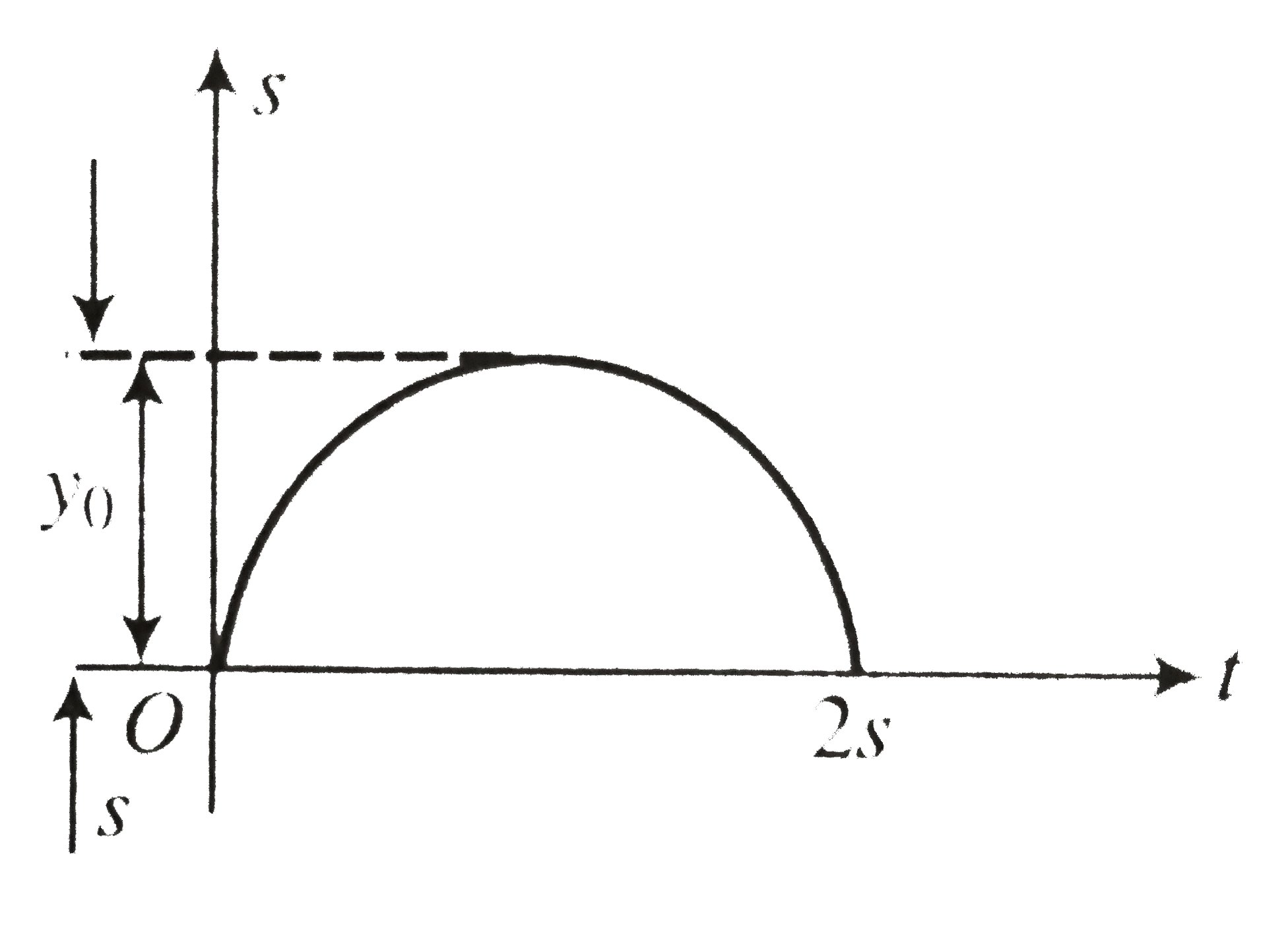View SolutionA particle is moving along x-axis such that its velocity varies with time according to v=(3m/s2)t−(2m/s3)t2. Find the velocity at t = 1 s and average velocity of the particle for the interval t = 0 to t = 5 s.
View SolutionThe position of a particle moving on X-axis is given by
x=At3+Bt2+Ct+D.
The numerical values of A,B,C,D are 1,4,-2 and 5 respectively and I units are used. Find a. the dimensions of A,B, C and D b. the velocity of the particle at t=4s, the acceleration of he particle at t=4s, d. The average velocity during the interval t=0 to t=4s, the average accelerationduring the interval t=0 to t=4s.View SolutionFind the velocity of a particle moving on a line at t = 3 seconds , if its position s is in m when
s = log t andView SolutionA one-dimensional force F varies with time according to the given graph. Calculate impulse of the force in following time intervals.
(a) From t=0s to t=10s.
From t=10s to t=15s.
(C) From t=0s to t=15s.View SolutionIf acceleration a(t)=3t2 and initial velocity u=0 m/s , then the velocity of the particle after time t=4 s
View SolutionFigure shows the velocity time graph for a particle travelling along a straight line. The magnitude of average velocity (in m/s) of particle during the time interval from t=0 to t=6s is 10α. Find the value of α.
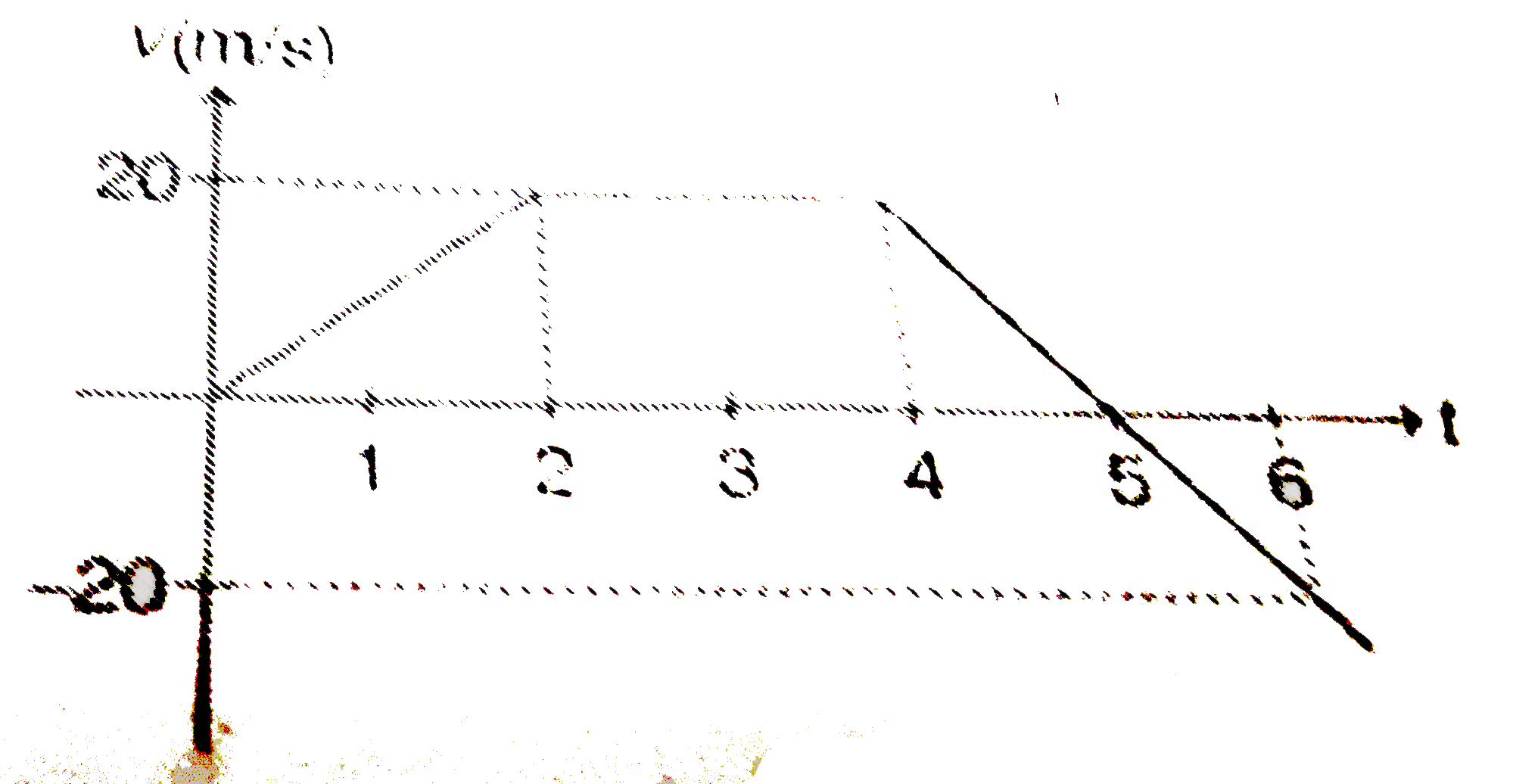View SolutionVelocity time equation of a particle moving in a straight line is v=2t−4 for t≤2s and v=4−2t for t>2.The distance travelled by the particle in the time interval from t=0 to t=4s is (Here t is in second and v in m/s)
View SolutionThe distance travelled by a particle in time t is given by s=(2.5ms2)t2. Find a. the average speed of the particle during the time 0 to 5.0 s, and b. the instantaneous speed ast t=5.0 is
View SolutionDisplacement of a particle of mass 2 kg varies with time as s=(2t2−2t+10)m. Find total work done on the particle in a time interval from t=0 to t=2s.
View Solution