If two circles touching both the axes intersect at two points P and Q where P=(3,1) then PQ=
√2
2√2
3√2
4√2
The correct Answer is:B
To find the length of segment PQ where P = (3, 1) and Q = (1, 3), we can use the distance formula. The distance formula between two points (x1, y1) and (x2, y2) is given by:
d=√(x2−x1)2+(y2−y1)2
1. Identify the coordinates of points P and Q:
- P = (3, 1)
- Q = (1, 3)
2. Substitute the coordinates into the distance formula:
- Here, x1=3, y1=1, x2=1, and y2=3.
- The distance PQ can be calculated as follows:
PQ=√(1−3)2+(3−1)2
3. Calculate the differences:
- x2−x1=1−3=−2
- y2−y1=3−1=2
4. Square the differences:
- (−2)2=4
- (2)2=4
5. Add the squared differences:
PQ=√4+4=√8
6. Simplify the square root:
PQ=√8=2√2
Final Answer:
The length of segment PQ is 2√2.
---
- P = (3, 1)
- Q = (1, 3)
- Here, x1=3, y1=1, x2=1, and y2=3.
- The distance PQ can be calculated as follows:
PQ=√(1−3)2+(3−1)2
- x2−x1=1−3=−2
- y2−y1=3−1=2
- (−2)2=4
- (2)2=4
PQ=√4+4=√8
PQ=√8=2√2
The length of segment PQ is 2√2.
Similar Questions
Two circles touching both the axes intersect at (3,-2) then the coordinates of their other point of intersection is
View SolutionTwo circles with centres A and B intersect each other at points P and Q. Prove that the centre-line AB bisects the common chord PQ perpendicularly.
View SolutionIf two circles touching both the axes are passing through (2,3) then length of their common chord is
View SolutionTwo circles with centres O and O' of radii 3 cm and 4 cm, respectively intersect at two points P and Q such that OP and O'P are tangents to the two circles. Find the length of common chord PQ.
View SolutionTwo circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see Fig. 10.40). Prove that ∠ACP =∠QCD.
View SolutionTwo circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see Figure). Prove that ∠ACP=∠QCD.
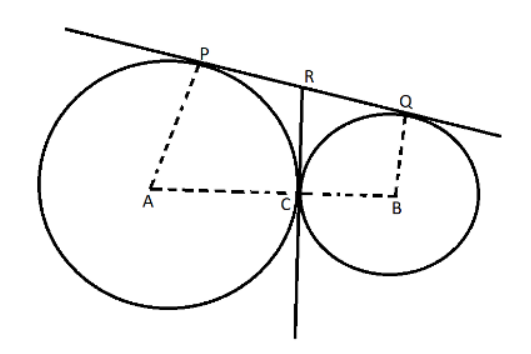
View SolutionIn the figure, two circles touch each other at the point C.Prove that the common tangents to the circles at C, bisect the common tangents at P and Q.
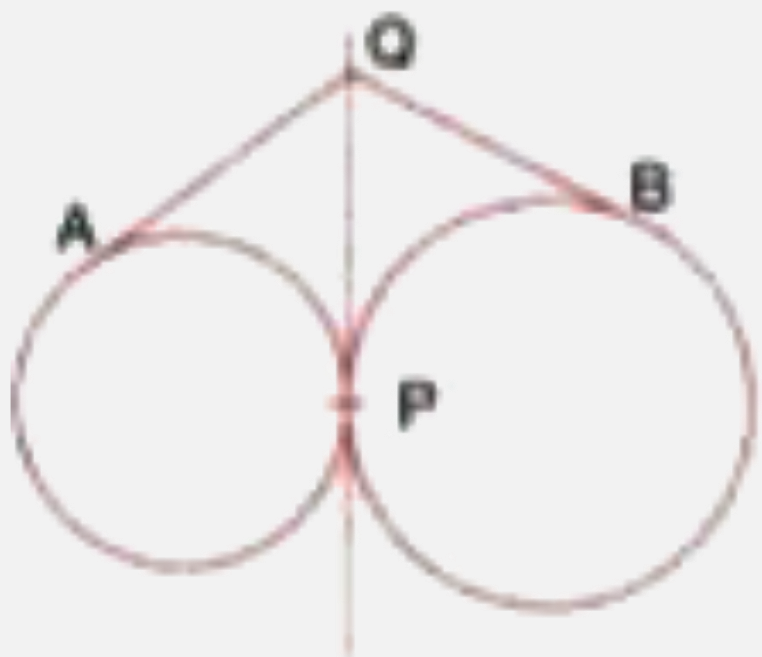
View SolutionTwo circles touch each other externally at point P. Q is a point on the common tangent through P. Prove that the tangents QA and QB are equal.
View SolutionIn Figure, two circles touch each other at the point C . Prove that the common tangent to the circles at C , bisects the common tangent at P and Q .
View SolutionPQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T . Find the length TP .
View Solution
