A system consists of n identical particles each of mass m. The total number of interaction potential energy terms possible are n(n−1)x. Find value of x.
nature of developing restoring forces
Inertia
Both 1 & 2
None
The correct Answer is:C
Step by step video & image solution for A system consists of n identical particles each of mass m. The total number of interaction potential energy terms possible are (n(n-1))/x. Find value of x. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-IA (Statement type questions:)18videos
WAVES
- BOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-IA (Matching )4videos
WAVES
- BOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-III (Doppler effect :)15videos
WAVES
- BOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - PROBLEMS (LEVEL - II)33videos
WAVE OPTICS
- BOOK - AAKASH SERIESCHAPTER - WAVES OPTICSEXERCISE - EXERCISE -III (POLARISITION)10videos
WAVES OPTICS
Similar Questions
The total number of orbitals possible for the quantum number n is
View SolutionFour particles each of mass m are kept at the four vertices of a square of side 'a' . Find gravitational potential energy of this system.
View SolutionEight particles of mass 'm' each are placed at the verties of a cube of side 'a' . Find gravitational potential energy of this system .
. View SolutionA particle of mass = 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is nπ5 second. Find value of n.
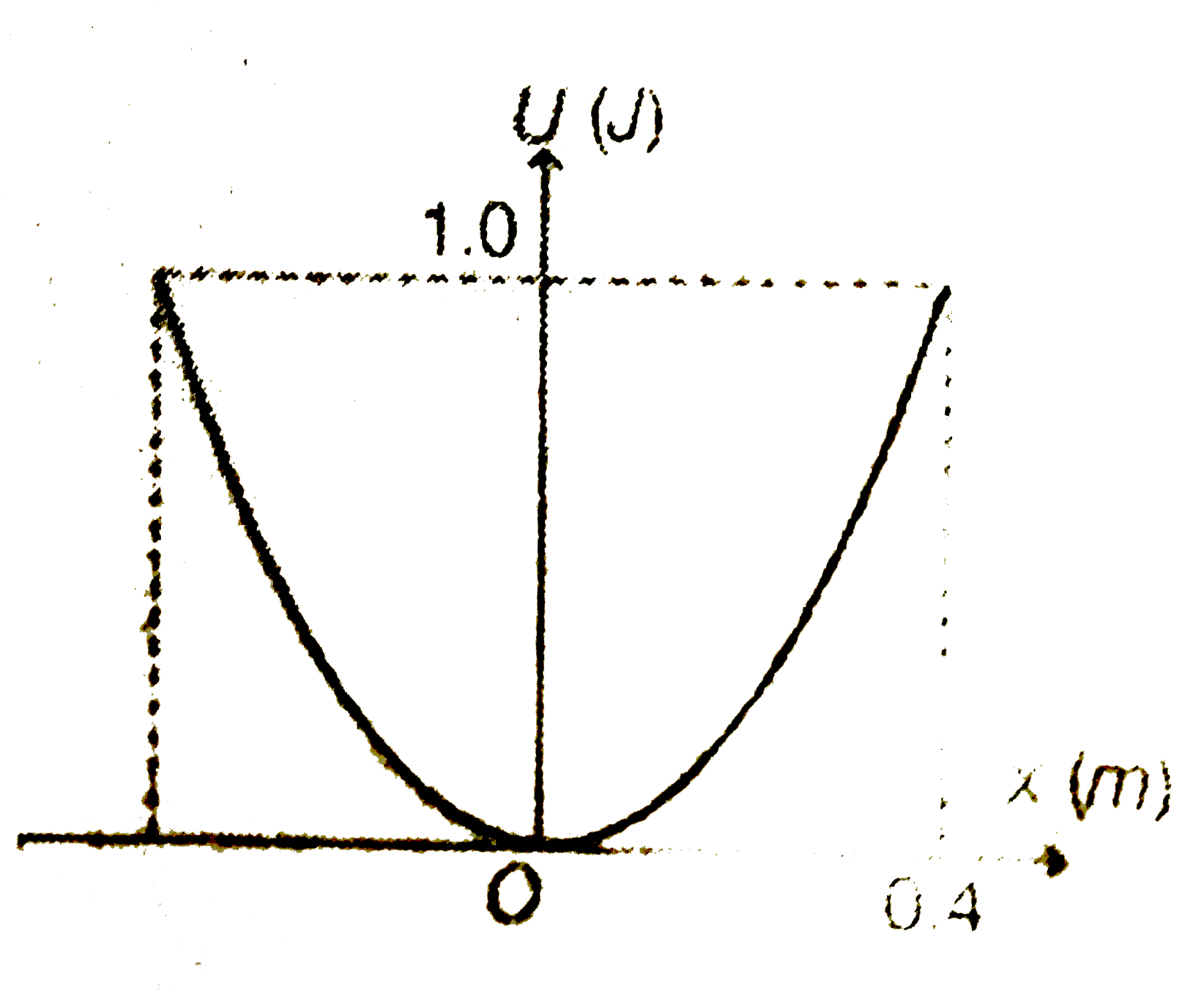View SolutionFind the potential energy of a system of four particles each of mass 2m kept at the vertices of a square of side x. Also find the potential at the centr of the square.
View SolutionFind the totoal number of distnct or
dissimilar terms in the expansion of
(x+y+z+w)n,n∈NView SolutionIf m and n are the two natural number such that mn=25, then find the value of nm:-
View SolutionIf the constant term in the binomial expansion of (x2−1x)n,n∈N is 15, then find the value of n.
View SolutionIf the constant term in the binomial expansion of (x2−1x)n,n∈N is 15, then find the value of n.
View SolutionStatement 1: The total number of dissimilar terms in the expansion of (x1+x2++xn)3isn(n+1)(n+2)6.
View Solution