(A ): Sharper is the curvature of spot on a charged body lesser will be the surface density of charge at that point.
(R ): Electric field is zero inside a charged conductor.
Both .A. and .R. are true and .R. is the correct explanation of .A.
Both .A. and .R. are tru and .R. is not the correct explanation of .A.
A. is true and .R. is false
A. is false and .R. is true
The correct Answer is:D
To solve the given question, we need to analyze both the assertion (A) and the reason (R) provided.
1. Understanding the Assertion (A):
- The assertion states: "Sharper is the curvature of a spot on a charged body, lesser will be the surface density of charge at that point."
- Surface charge density (σ) is defined as the amount of charge (Q) per unit area (A) on the surface:
σ=QA
- If the curvature of a spot is sharper, it implies that the area (A) at that point is smaller.
2. Analyzing the Relationship:
- Since surface charge density is inversely proportional to the area:
- If the area (A) is smaller (due to sharper curvature), the surface charge density (σ) must be greater, not lesser.
- Therefore, the assertion is incorrect because it states the opposite.
3. Understanding the Reason (R):
- The reason states: "Electric field is zero inside a charged conductor."
- According to electrostatic principles, when a conductor is charged, the charges redistribute themselves on the surface of the conductor.
- Inside the conductor, the electric field (E) is indeed zero because the charges balance out any internal electric fields.
4. Conclusion:
- Assertion (A) is false because it incorrectly states the relationship between curvature and surface charge density.
- Reason (R) is true as it accurately describes the behavior of electric fields inside a charged conductor.
- Therefore, the correct conclusion is that A is false and R is true.
Final Answer:
- Assertion (A) is false.
- Reason (R) is true.
- The assertion states: "Sharper is the curvature of a spot on a charged body, lesser will be the surface density of charge at that point."
- Surface charge density (σ) is defined as the amount of charge (Q) per unit area (A) on the surface:
σ=QA
- If the curvature of a spot is sharper, it implies that the area (A) at that point is smaller.
- Since surface charge density is inversely proportional to the area:
- If the area (A) is smaller (due to sharper curvature), the surface charge density (σ) must be greater, not lesser.
- Therefore, the assertion is incorrect because it states the opposite.
- The reason states: "Electric field is zero inside a charged conductor."
- According to electrostatic principles, when a conductor is charged, the charges redistribute themselves on the surface of the conductor.
- Inside the conductor, the electric field (E) is indeed zero because the charges balance out any internal electric fields.
- Assertion (A) is false because it incorrectly states the relationship between curvature and surface charge density.
- Reason (R) is true as it accurately describes the behavior of electric fields inside a charged conductor.
- Therefore, the correct conclusion is that A is false and R is true.
- Assertion (A) is false.
- Reason (R) is true.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - AAKASH SERIESCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Exercise-II
56 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - AAKASH SERIESCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Exercise
57 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - AAKASH SERIESCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Assess Your Self
13 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - AAKASH SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - PRACTICE EXERCISEX
42 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-II)
26 Videos
Similar Questions
Across the surface of a charged conductor, the electric
View SolutionIn the following question a statement of assertion (A) is followed by a statement of reason (R )
A : Electric field is discontinuous across the surface of a charged conductor.
R : Electric potential is discontinuous across the surface of a charged conductor .
View SolutionA charge q kept in front of a neutral metallic sphere. Find the electric field at the centre of sphere due to the induced charges on the surface of the sphere shown.
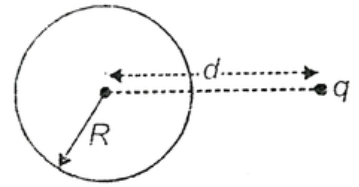
Strategy : The net electric field inside the conductor is zero. This is produced by induced charges and the external charge.
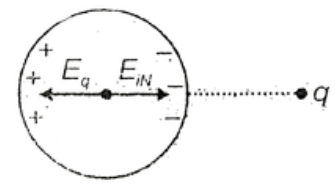
View SolutionA charge q kept in front of a neutral metallic sphere. Find the electric field at the centre of sphere due to the induced charges on the surface of the sphere shown.

Strategy : The net electric field inside the conductor is zero. Thsi is produced by induced charges and the external charge.

View SolutionA positive point charge (+q) is kept in the vicinity of an uncharged conducting plate. Sketch electric field lines originating from the point on to the surface of the plate.
Derive the expression for the electric field at the surface of a charged conductor.
View SolutionA point charge is brought in an electric field. The electric field at a near by point
View SolutionA number of spherical conductors of different radii are charged to same potential. The surface charge density of each conductor is related with its radius as
View SolutionThe figure shows a charge q placed inside a cavity in an uncharged conductor. Now if an external electric field is swiched on

View SolutionTwo charges e and 3e are placed at a distance r. The distance of the point where the electric field intensity will be zero is
View SolutionA spherical conducting shell of inner radius r1 and outer radius r2 has a charge Q.
(a) A charge q is placed at the center of the shell. What is the surface charge density on the inner and outer surfaces of the shell ?
(b) Is the electric field intensity inside a cavity (with no charge) zero, even if the shell is not spherical, but has any irregular shape ? Explain.
View Solution
