The force between two electrons when placed in air is equal to 0.5 times the weight of an electron. Find the distance between two electrons (mass of electron =9.1×10−31kg)
7.2m
72m
72m.
720m
The correct Answer is:A
To solve the problem, we need to find the distance between two electrons given that the electrostatic force between them is equal to 0.5 times the weight of an electron.
1. Identify the weight of an electron:
The weight (W) of an electron can be calculated using the formula:
W=m⋅g
where m is the mass of the electron and g is the acceleration due to gravity (approximately 10m/s2).
Given m=9.1×10−31kg:
W=9.1×10−31kg×10m/s2=9.1×10−30N
2. Calculate the electrostatic force:
According to the problem, the electrostatic force (F) between the two electrons is:
F=0.5×W=0.5×9.1×10−30N=4.55×10−30N
3. Use Coulomb's Law:
The electrostatic force between two point charges (in this case, two electrons) is given by Coulomb's Law:
F=14πϵ0e2r2
where:
- e is the charge of an electron, approximately 1.6×10−19C
- ϵ0 is the permittivity of free space, approximately 8.85×10−12C2/N m2
4. Substituting values into Coulomb's Law:
Rearranging the equation to solve for r:
r2=14πϵ0e2F
Substituting in the known values:
r2=14π(8.85×10−12)(1.6×10−19)24.55×10−30
5. Calculating r2:
First, calculate (1.6×10−19)24.55×10−30:
(1.6×10−19)2=2.56×10−38
2.56×10−384.55×10−30≈5.62×10−9
Now calculate 4π(8.85×10−12):
4π(8.85×10−12)≈1.11×10−10
Therefore,
r2=5.62×10−91.11×10−10≈50.63
6. Taking the square root:
r=√50.63≈7.115m
7. Final answer:
Rounding this to one decimal place gives:
r≈7.2m
Conclusion:
The distance between the two electrons is approximately 7.2 meters.
The weight (W) of an electron can be calculated using the formula:
W=m⋅g
where m is the mass of the electron and g is the acceleration due to gravity (approximately 10m/s2).
Given m=9.1×10−31kg:
W=9.1×10−31kg×10m/s2=9.1×10−30N
According to the problem, the electrostatic force (F) between the two electrons is:
F=0.5×W=0.5×9.1×10−30N=4.55×10−30N
The electrostatic force between two point charges (in this case, two electrons) is given by Coulomb's Law:
F=14πϵ0e2r2
where:
- e is the charge of an electron, approximately 1.6×10−19C
- ϵ0 is the permittivity of free space, approximately 8.85×10−12C2/N m2
Rearranging the equation to solve for r:
r2=14πϵ0e2F
Substituting in the known values:
r2=14π(8.85×10−12)(1.6×10−19)24.55×10−30
First, calculate (1.6×10−19)24.55×10−30:
(1.6×10−19)2=2.56×10−38
2.56×10−384.55×10−30≈5.62×10−9
Now calculate 4π(8.85×10−12):
4π(8.85×10−12)≈1.11×10−10
Therefore,
r2=5.62×10−91.11×10−10≈50.63
r=√50.63≈7.115m
Rounding this to one decimal place gives:
r≈7.2m
The distance between the two electrons is approximately 7.2 meters.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - AAKASH SERIESCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Exercise
57 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - AAKASH SERIESCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Exercise-I
80 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - AAKASH SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - PRACTICE EXERCISEX
42 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-II)
26 Videos
Similar Questions
The force between two electrons separated by a distance r varies as
View SolutionThe force between two electrons separated by a distance r is proportional to
View SolutionCalculate the ratio of electric to gravitational force between two electrons.
View SolutionDetermine the de Broglie wavelength of a proton, whose kinetice energy is equal to the rest of the mass energy of an electron. Given that the mass of an electron is 9×10−31 kg and the mass of a proton is 1837 times as that of the electron.
View SolutionThe mass of half mole of electrons is about (Given: Mass of electron =9.1×10−28 g)
View SolutionThe speed of an electron in the inner most orbit of the hydrogen (Bohr radius = 52.9 pm, me =9.11×10−31kg) is
View SolutionA microscope using suitable photons is employed to an electron in an atom within a distance of 0.1Å. What is the uncertainty involved in the measurment of its velocity? Mass of electron =9.11×10−31kg and h=6.626×10−34Js
View SolutionAn electron is projected with an initial speed v0=1.60×106ms−1 into the uniform field between the parallel plates as shown in fig. Assume that the field between the plates is uniform and directed vertically downward, and that the field outside the plates is zero. the electrons enters the field at a point midway between the plates. Mass of electron is 9.1×10−31kg.
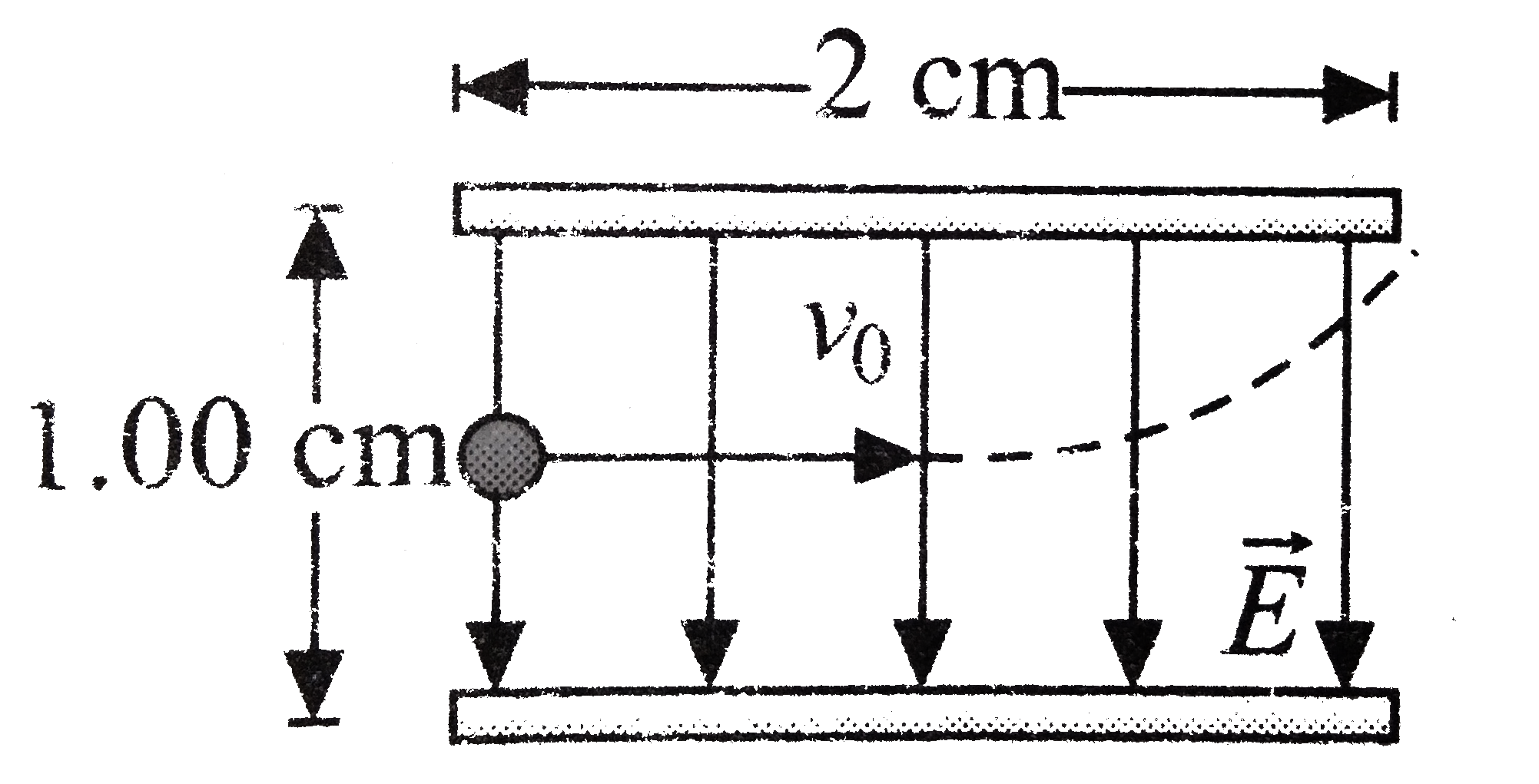
The vertical displacement traveled by the proton as it exits the region between the plated is (mass pf proton is 1.67×10−27kg).
View SolutionAn electron is projected with an initial speed v0=1.60×106ms−1 into the uniform field between the parallel plates as shown in fig. Assume that the field between the plates is uniform and directed vertically downward, and that the field outside the plates is zero. the electrons enters the field at a point midway between the plates. Mass of electron is 9.1×10−31kg.

The vertical displacement traveled by the proton as it exits the region between the plated is (mass pf proton is 1.67×10−27kg).
View SolutionAn electron moving along the x-axis with an initial energy of 100eV enters a region of magnetic field →B=(1.5×10−3T)ˆk at S (see figure). The field extends between x=0 and x=2cm. The electron is detected at the point Q on a screen placed 8 cm away from the point S. The distance d between P and Q (on the screen) is :
(electron's charge =1.6×10−19C, mass of electron =9.1×10−31kg).
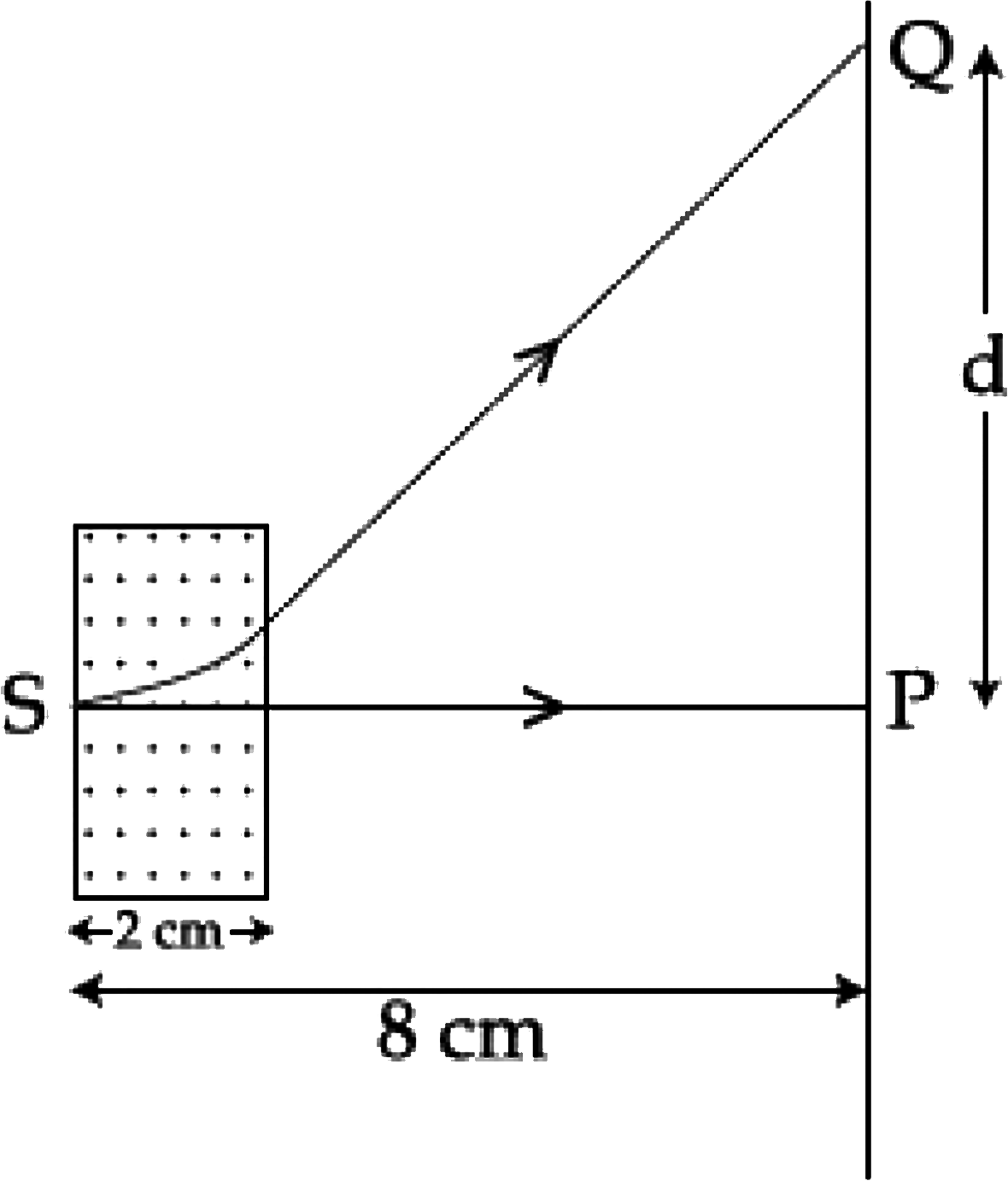 a) 11.65cm. b) 12.87 cm
c) 1.22cm
d) 2.25cm
a) 11.65cm. b) 12.87 cm
c) 1.22cm
d) 2.25cm
View Solution
