A planet of small mass m moves around the sun of mass M, along an elliptical orbit such that its minimum and maximum distance from sun are r and R, respectively. Its period of revolution will be:
T=2πr(m/2kλq)1/2
T2=4π2mr3/2qkλ
T=1/2πr(2kλq/m)1/2
T=1/2πr(m/kπλq)1/2where K=14πε0
The correct Answer is:A
Step by step video & image solution for A planet of small mass m moves around the sun of mass M, along an elliptical orbit such that its minimum and maximum distance from sun are r and R, respectively. Its period of revolution will be: by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -II LECTURE SHEET (ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS)
20 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -II LECTURE SHEET (ADVANCED) MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)
4 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - PRACTICE SHEET (EXERCISE -V ELECTRIC DIPOLE) (LEVEL -II INTEGER TYPE QUESTION)
2 Videos
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - ADDITIONAL EXERCISE
13 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
10 Videos
Similar Questions
A planet of small mass m moves around the sun of mass M along an elliptrical orbit such that its minimum and maximum distance from sun are r and R respectively. Its period of revolution will be:
View SolutionA planet of mass m moves around the Sun of mass Min an elliptical orbit. The maximum and minimum distance of the planet from the Sun are r1 and r2, respectively. Find the relation between the time period of the planet in terms of r1 and r2.
View Solution
Knowledge Check
A planet revolves around the sun in an elliptical orbit. Suppose that the gravitational attraction between the sun and the planet suddenly disappear then the planet would move
Atowards the sun in a spiral pathBaway from the sun along a straight path with continuously increasing speedCwith constant speed along a tangential path to the oribtDtowards the sun along a straight path with constant speedA planet revolves around the sun in an elliptical orbit. If vp and va are the velocities of the planet at the perigee and apogee respectively, then the eccentricity of the elliptical orbit is given by :
AvpvaBva−vpva+vpCvp+vavp−vaDvp−vavp+va
A planet of mass m moves along an ellipse around the sum of mass M so that its maximum and minimum distances from sum are a and b respectively. Prove that the angular momentum L of this planet relative to the centre of the sun is L=m√2GMab(a+b)
View SolutionA planet of mass m revolves in elliptical orbit around the sun of mass M so that its maximum and minimum distance from the sun equal to ra and rp respectively. Find the angular momentum of this planet relative to the sun.
View SolutionA planet of mass m is moving in an elliptical orbit about the sun (mass of sun = M). The maximum and minimum distances of the planet from the sun are r1 and r2 respectively. The period of revolution of the planet wil be proportional to :
View SolutionA planet of mass m moves along an ellipse around the Sun so that its maximum and minimum distances from the Sun are equal to r1 and r2 respectively. Find the angular momentum M of this planet relative to the centre of the Sun.
View SolutionA planet is moving round the sun in an elliptical orbit as shows. As the planet moves from A to B
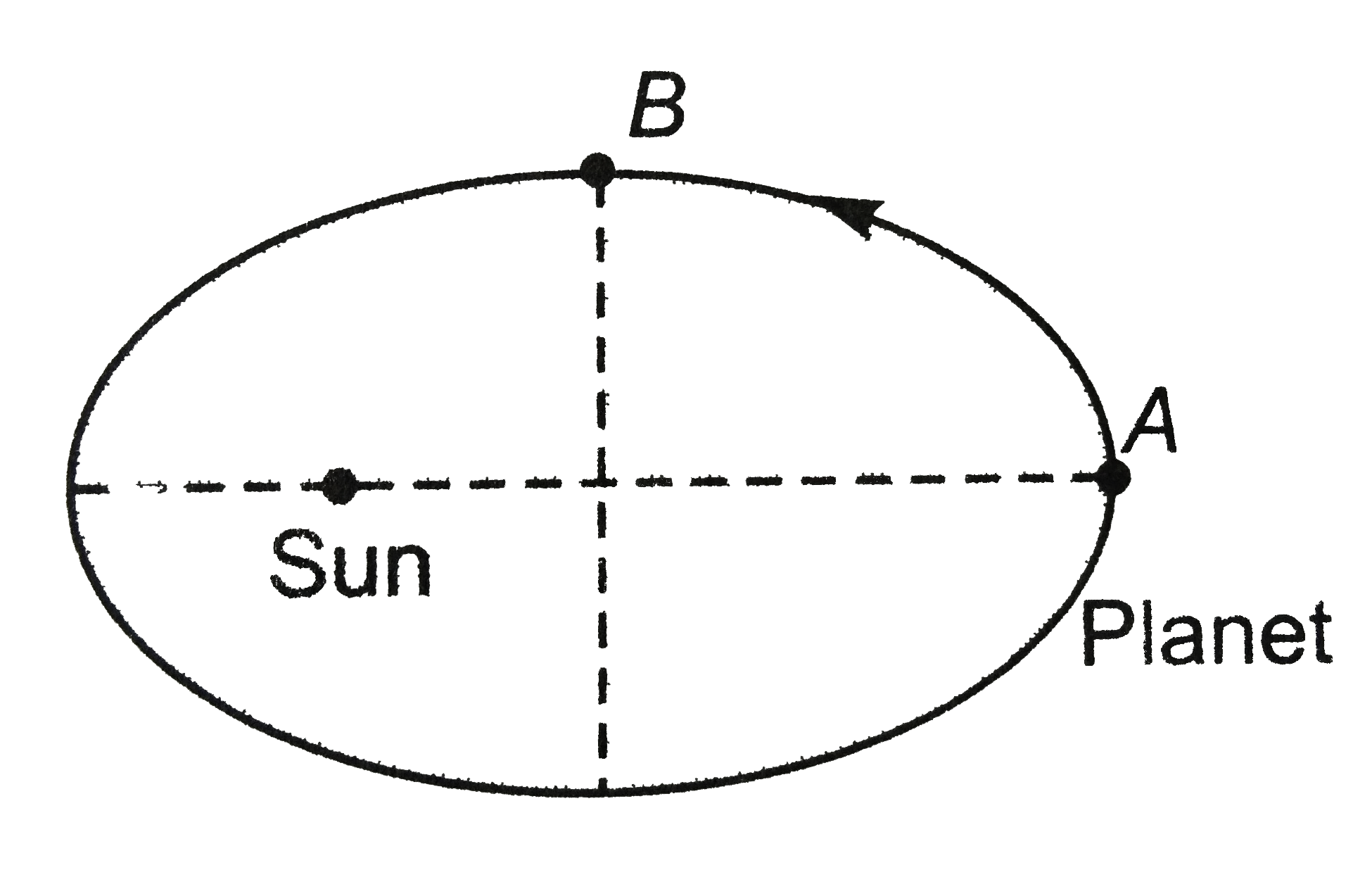
View SolutionSpeed of a planet in an ellioptical orbit with semimajor axis a about sun of mass M at a distance r from sun is
View Solution
