Each of the two long parallel threads carries a uniform λ per unit length. The threads are separated by a distance l. Find the maximum magnitude of the electric field strenght in the symmetry plane of this system located between the threads.
Emax=λ/2πε0l
Emax=λ/3πε0l
Emax=λ/πε0
Emax=λ/πε0l
The correct Answer is:D
To find the maximum magnitude of the electric field strength in the symmetry plane located between two long parallel threads carrying a uniform linear charge density (λ), we can follow these steps:
Step 1: Understanding the Setup
We have two long parallel threads separated by a distance l, each carrying a uniform charge density λ per unit length. The symmetry plane is located exactly in the middle of the two threads.
Step 2: Electric Field Due to a Single Thread
The electric field E due to a single long charged thread at a distance r from it is given by the formula:
E=λ2πϵ0r
where ϵ0 is the permittivity of free space.
Step 3: Determine the Position in the Symmetry Plane
In the symmetry plane, the distance from each thread to the midpoint is l2.
Step 4: Calculate the Electric Field Contributions
1. Electric Field from the First Thread: The electric field E1 at the midpoint due to the first thread (to the right) is:
E1=λ2πϵ0(l2)=λπϵ0l
2. Electric Field from the Second Thread: The electric field E2 at the midpoint due to the second thread (to the left) is:
E2=λ2πϵ0(l2)=λπϵ0l
Step 5: Direction of the Electric Fields
- The electric field due to the first thread points away from the thread (to the right).
- The electric field due to the second thread also points away from the thread (to the left).
Step 6: Net Electric Field in the Symmetry Plane
Since both electric fields are in the same direction (away from the threads), the total electric field Etotal at the midpoint is:
Etotal=E1+E2=λπϵ0l+λπϵ0l=2λπϵ0l
Step 7: Conclusion
The maximum magnitude of the electric field strength in the symmetry plane located between the threads is:
Emax=2λπϵ0l
Final Answer
The maximum magnitude of the electric field strength in the symmetry plane is:
Emax=2λπϵ0l
---
We have two long parallel threads separated by a distance l, each carrying a uniform charge density λ per unit length. The symmetry plane is located exactly in the middle of the two threads.
The electric field E due to a single long charged thread at a distance r from it is given by the formula:
E=λ2πϵ0r
where ϵ0 is the permittivity of free space.
In the symmetry plane, the distance from each thread to the midpoint is l2.
1. Electric Field from the First Thread: The electric field E1 at the midpoint due to the first thread (to the right) is:
E1=λ2πϵ0(l2)=λπϵ0l
E2=λ2πϵ0(l2)=λπϵ0l
- The electric field due to the first thread points away from the thread (to the right).
- The electric field due to the second thread also points away from the thread (to the left).
Since both electric fields are in the same direction (away from the threads), the total electric field Etotal at the midpoint is:
Etotal=E1+E2=λπϵ0l+λπϵ0l=2λπϵ0l
The maximum magnitude of the electric field strength in the symmetry plane located between the threads is:
Emax=2λπϵ0l
The maximum magnitude of the electric field strength in the symmetry plane is:
Emax=2λπϵ0l
Topper's Solved these Questions
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -II LECTURE SHEET (ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS)
20 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -II LECTURE SHEET (ADVANCED) MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)
4 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - PRACTICE SHEET (EXERCISE -V ELECTRIC DIPOLE) (LEVEL -II INTEGER TYPE QUESTION)
2 Videos
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - ADDITIONAL EXERCISE
13 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
10 Videos
Similar Questions
Each of two long parallel wires carries a constant current i along the same direction . The wires are separated by a distance 2I. The magnitude of resultant magnetic induction in the symmetric plane of this system located between the wires at a distance R from each wire will be
View SolutionA long string with a charge of λ per unit length passes through an imaginary cube of edge a. The maximum flux of the electric field through the cube will be
View Solution
Knowledge Check
Two infinite plane parallel sheets, separated by a distance d have equal and opposite uniform charge densities σ. Electric field at a point between the sheets is
Aσ2ε0Bσε0CzeroDdepends on the location of the point
Two parallel wires carry equal currents of 10A along the same direction and are separated by a distance of 2.0 cm. Find the magnetic field at a point which is 2.0 cm away from each of these wires.
View SolutionA thread carrying a unifrom charge λ per unit length has the configuration shown in fig, Assuming a curvature radius R to be considerably less than the length of the thread, find the magnitude fo the electric field strength at the point O.
 ,
, 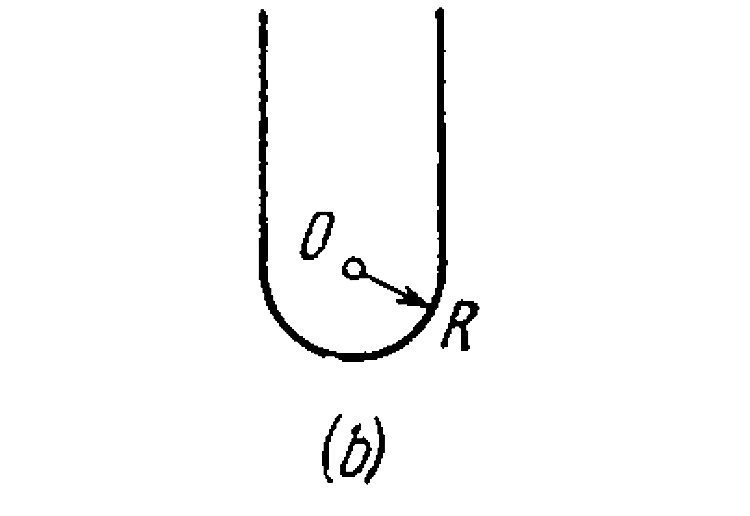
View SolutionA very long straight uniformly charged thread carries a charge λ per unit length, Find the magnitude and direction of the electric field strenght at a point which is at a distance y from the thread and lies on the perpendicular passing through one of the thread.s ends.
View SolutionTwo long parallel copper wires carry current of 5A each in opposite directions. If the wires are separated by a distance distance of 0.5m, then the force per unit length between the two wires is
View SolutionTwo thin long parallel wires seperated by a distance 'b' are carrying a current ' I' amp each . The magnitude of the force3 per unit length exerted by one wire on the other is
View SolutionTwo infinitely long rods carry equal linear denisty λ each. They are perpendicular to each other and they are in different planes and separated by a distance d. Find the electrostatic force on once rod due to the other
View SolutionA uniform solid cylinder of mass m rests on two horizontal planks. A thread is wound on the cylinder. The hanging end of the thread is pulled vertically down with a constant force F.
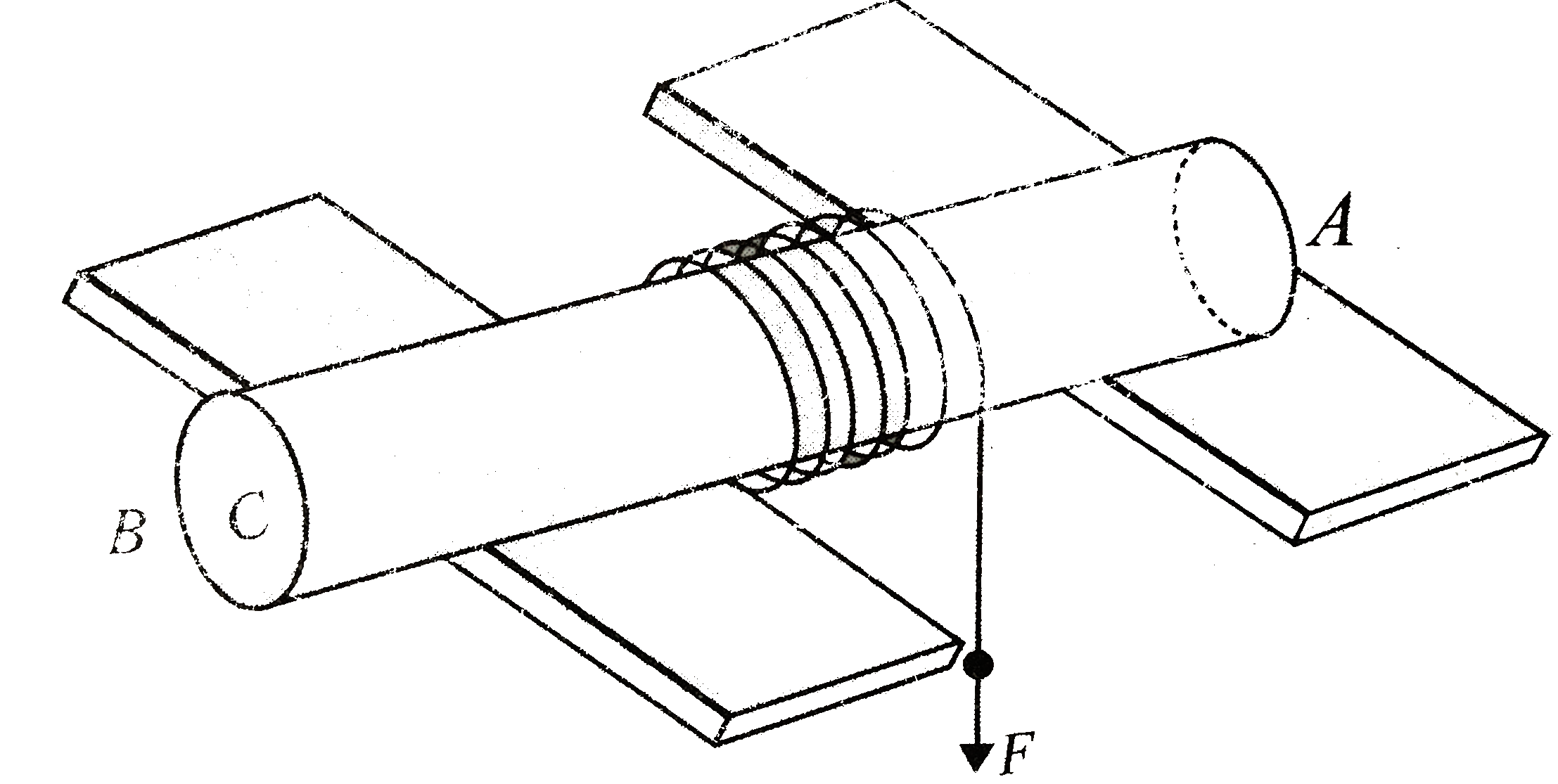
Find the maximum magnitude of the force F which may be applied without bringing about any sliding of the cylinder, if the coefficient of friction between the plank and the cylinder is equal to μ. What is the maximum acceleration of the centre of mass over the planks?
View Solution
