A thin wire of linear charge density λ is bent in the form of a triangle ABC and an imaginary cube of side .a. is taken with vertex A at the centre of the top face and vertices B,C at the opposite edge centres of the bottom face. The total electric flux linked with the cube is
λa(√3+1)∈0
λa(√3+12)∈0
λa(√5+1)∈0
λa(√5+12)∈0
The correct Answer is:C
To solve the problem of finding the total electric flux linked with the cube due to a thin wire of linear charge density λ bent in the form of a triangle ABC, we can follow these steps:
1. Understanding the Configuration:
- We have a triangle ABC formed by a thin wire with linear charge density λ.
- The cube has a side length a, with vertex A at the center of the top face and vertices B and C at the centers of the opposite edges of the bottom face.
2. Using Gauss's Law:
- According to Gauss's Law, the total electric flux (Φ) through a closed surface is given by:
\(
\Phi = \frac{Q_{\text{enclosed}}}{\epsilon_0}
\)
- Here, \(Q_{\text{enclosed}}\) is the total charge enclosed by the Gaussian surface.
3. Finding the Total Charge Enclosed:
- The total charge \(Q_{\text{enclosed}}\) can be calculated as:
\(
Q_{\text{enclosed}} = \lambda \cdot L
\)
- Where \(L\) is the total length of the wire that is enclosed within the cube.
4. Calculating the Length of the Wire:
- The triangle ABC has sides AB, AC, and BC.
- We know that BC = a (the side of the cube).
- To find AB and AC, we can use the Pythagorean theorem. The height from A to BC can be determined as follows:
- The distance from A to the midpoint of BC (let's call it P) is the height of the triangle.
- Since B and C are at the centers of the edges of the bottom face, the coordinates of B and C can be taken as \((-\frac{a}{2}, 0, 0)\) and \((\frac{a}{2}, 0, 0)\).
- The length AP = a (the height of the triangle).
- The distance from P to B (or C) is \(\frac{a}{2}\).
5. Finding Lengths AB and AC:
- Using the Pythagorean theorem:
\(
AB = AC = \sqrt{AP^2 + PB^2} = \sqrt{a^2 + \left(\frac{a}{2}\right)^2} = \sqrt{a^2 + \frac{a^2}{4}} = \sqrt{\frac{5a^2}{4}} = \frac{a\sqrt{5}}{2}
\)
- Thus, the total length of the wire \(L\) is:
\(
L = AB + AC + BC = \frac{a\sqrt{5}}{2} + \frac{a\sqrt{5}}{2} + a = a\sqrt{5} + a = a(\sqrt{5} + 1)
\)
6. Calculating Total Charge Enclosed:
- Now substituting back into the charge equation:
\(
Q_{\text{enclosed}} = \lambda \cdot a(\sqrt{5} + 1)
\)
7. Finding Total Electric Flux:
- Finally, substituting \(Q_{\text{enclosed}}\) into Gauss's Law:
\(
\Phi = \frac{Q_{\text{enclosed}}}{\epsilon_0} = \frac{\lambda \cdot a(\sqrt{5} + 1)}{\epsilon_0}
\)
Final Answer:
Thus, the total electric flux linked with the cube is:
\(
\Phi = \frac{\lambda a (\sqrt{5} + 1)}{\epsilon_0}
\)
- We have a triangle ABC formed by a thin wire with linear charge density λ.
- The cube has a side length a, with vertex A at the center of the top face and vertices B and C at the centers of the opposite edges of the bottom face.
- According to Gauss's Law, the total electric flux (Φ) through a closed surface is given by:
\(
\Phi = \frac{Q_{\text{enclosed}}}{\epsilon_0}
\)
- Here, \(Q_{\text{enclosed}}\) is the total charge enclosed by the Gaussian surface.
- The total charge \(Q_{\text{enclosed}}\) can be calculated as:
\(
Q_{\text{enclosed}} = \lambda \cdot L
\)
- Where \(L\) is the total length of the wire that is enclosed within the cube.
- The triangle ABC has sides AB, AC, and BC.
- We know that BC = a (the side of the cube).
- To find AB and AC, we can use the Pythagorean theorem. The height from A to BC can be determined as follows:
- The distance from A to the midpoint of BC (let's call it P) is the height of the triangle.
- Since B and C are at the centers of the edges of the bottom face, the coordinates of B and C can be taken as \((-\frac{a}{2}, 0, 0)\) and \((\frac{a}{2}, 0, 0)\).
- The length AP = a (the height of the triangle).
- The distance from P to B (or C) is \(\frac{a}{2}\).
- Using the Pythagorean theorem:
\(
AB = AC = \sqrt{AP^2 + PB^2} = \sqrt{a^2 + \left(\frac{a}{2}\right)^2} = \sqrt{a^2 + \frac{a^2}{4}} = \sqrt{\frac{5a^2}{4}} = \frac{a\sqrt{5}}{2}
\)
- Thus, the total length of the wire \(L\) is:
\(
L = AB + AC + BC = \frac{a\sqrt{5}}{2} + \frac{a\sqrt{5}}{2} + a = a\sqrt{5} + a = a(\sqrt{5} + 1)
\)
- Now substituting back into the charge equation:
\(
Q_{\text{enclosed}} = \lambda \cdot a(\sqrt{5} + 1)
\)
- Finally, substituting \(Q_{\text{enclosed}}\) into Gauss's Law:
\(
\Phi = \frac{Q_{\text{enclosed}}}{\epsilon_0} = \frac{\lambda \cdot a(\sqrt{5} + 1)}{\epsilon_0}
\)
Thus, the total electric flux linked with the cube is:
\(
\Phi = \frac{\lambda a (\sqrt{5} + 1)}{\epsilon_0}
\)
Topper's Solved these Questions
- ELECTROSTATICSBook:AAKASH SERIESChapter:ELECTROSTATICSExercise:ADDITIONAL PRACTICE EXERCISE (LEVEL -II LECTURE SHEET (ADVANCED) MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)
Explore 4 Videos
- ELECTROSTATICSBook:AAKASH SERIESChapter:ELECTROSTATICSExercise:ADDITIONAL PRACTICE EXERCISE (LEVEL -II LECTURE SHEET (ADVANCED) LINKED COMPREHENSION TYPE QUESTIONS)
Explore 2 Videos
- ELECTROSTATICSBook:AAKASH SERIESChapter:ELECTROSTATICSExercise:ADDITIONAL PRACTICE EXERCISE (LEVEL - I (MAIN) (STRAIGHT OBJECTIVE TYPE QUESTIONS)
Explore 24 Videos
- ELECTROMAGNETICSBook:AAKASH SERIESChapter:ELECTROMAGNETICSExercise:ADDITIONAL EXERCISE
Explore 13 Videos
- ELEMENTS OF VECTORSBook:AAKASH SERIESChapter:ELEMENTS OF VECTORSExercise:QUESTIONS FOR DESCRIPTIVE ANSWERS
Explore 10 Videos
Similar Questions
A charge Q is situated at the centre of a cube. The electric flux through one of the faces of the cube is
View SolutionA charge q is located at the centre of a cube. The electric flux through any face is
View SolutionA charge q is located at the centre of a cube. The electric flux through any face is
View SolutionA charge qμC is placed at the centre of a cube of a side 0.1m, then the electric flux diverging from each face of the cube is
View SolutionCharge of 2 C is placed at the centre of a cube. What is the electric flux passing through one face ?
View SolutionA charge is placed at the centre of cube of side a then flux linked with one of its given faces will be
View SolutionA charge Q is placed at the corner of a cube of edge length L. The electric flux linked to one of the faces not touching the charge Q is
View SolutionIf charges q/2 and 2q are placed at the centre of face and at the corner of a cube, then the total flux through the cube will be
View SolutionIf a point charge q is placed at the centre of a cube.
What is the flux linked (a) with the cube? (b) with each face of the cube?
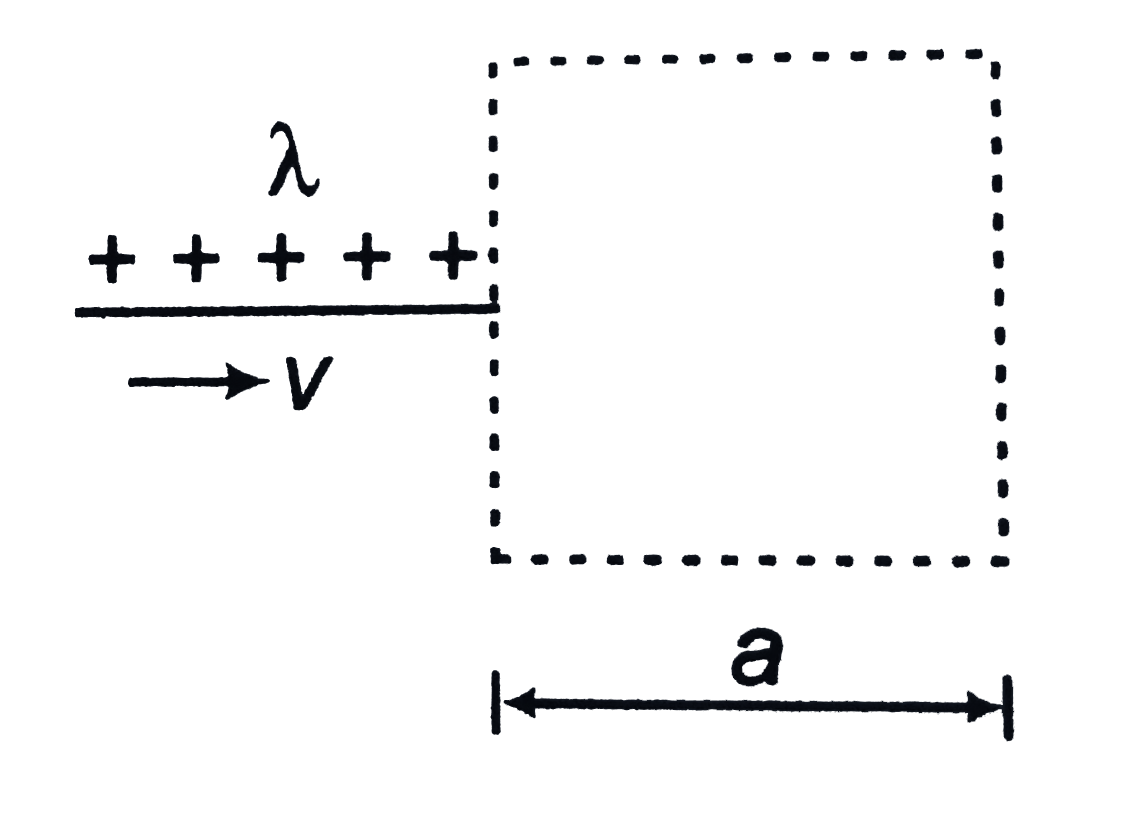
View SolutionFigure shows an imaginary cube of side a. A uniformly charged rod of length a moves towards right at a constant speed v. At t=0 the right end of the just touches the left face of the cube. Plot a graph between electric flux passing through the cube versus time.
View Solution