A 4μF capacitor is charged by a 200 V battery. It is then disconnected from the supply and is connected to another uncharged 2μF capacitor. During the process loss of energy (in J) s
Zero
5.33×10−2
4×10−2
2.67×10−2
The correct Answer is:D
To solve the problem step by step, we will calculate the initial energy stored in the first capacitor, find the new voltage after connecting the second capacitor, calculate the energy stored in the system after the connection, and finally determine the loss of energy.
Step 1: Calculate the initial energy stored in the first capacitor (U1)
The formula for the energy stored in a capacitor is given by:
U=12CV2
Where:
- C is the capacitance in farads (F)
- V is the voltage in volts (V)
For the first capacitor:
- C1=4μF=4×10−6F
- V1=200V
Substituting these values into the formula:
U1=12×4×10−6×(200)2
Calculating (200)2:
(200)2=40000
Now substituting:
U1=12×4×10−6×40000
U1=2×10−6×40000=8×10−2J
Step 2: Calculate the new voltage (V2) after connecting the second capacitor
When the charged capacitor is connected to an uncharged capacitor, charge conservation applies. The total charge before connection is equal to the total charge after connection.
The charge Q on the first capacitor is:
Q=C1×V1=4×10−6×200=8×10−4C
After connecting the second capacitor C2=2μF=2×10−6F, the total capacitance Ctotal becomes:
Ctotal=C1+C2=4×10−6+2×10−6=6×10−6F
The new voltage V2 can be calculated using the formula:
V2=QCtotal=8×10−46×10−6=86×102=43×100=4003V
Step 3: Calculate the energy stored in the system after connection (U2)
Using the total capacitance and the new voltage:
U2=12CtotalV22
Substituting the values:
U2=12×6×10−6×(4003)2
Calculating (4003)2:
(4003)2=1600009
Now substituting:
U2=12×6×10−6×1600009
U2=3×10−6×1600009=4800009×10−6=163×10−2J
Step 4: Calculate the loss of energy (ΔU)
The loss of energy is given by:
ΔU=U1−U2
Substituting the values we calculated:
ΔU=8×10−2−163×10−2
Finding a common denominator (3):
ΔU=243×10−2−163×10−2=83×10−2J
Calculating the numerical value:
ΔU≈2.67×10−2J
Final Answer
The loss of energy during the process is approximately:
ΔU≈0.0267J
- C is the capacitance in farads (F)
- V is the voltage in volts (V)
- C1=4μF=4×10−6F
- V1=200V
U1=2×10−6×40000=8×10−2J
U2=3×10−6×1600009=4800009×10−6=163×10−2J
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - CAPACITORS EXERCISE - PRACTICE SHEET (EXERCISE - III) (LEVEL - II (ADVANCED)) (More than One correct answer Type Questions)7videos
CAPACITORS
- BOOK - AAKASH SERIESCHAPTER - CAPACITORS EXERCISE - PRACTICE SHEET (EXERCISE - III) (LEVEL - II (ADVANCED)) (Linked Comprehension Type Questions)6videos
CAPACITORS
- BOOK - AAKASH SERIESCHAPTER - CAPACITORS EXERCISE - PRACTICE SHEET (EXERCISE - II) (LEVEL - II (ADVANCED)) (Straight Objective Type Questions)5videos
CAPACITORS
- BOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - PRACTICE EXERCISE21videos
ATOMS
- BOOK - AAKASH SERIESCHAPTER - COMMUNICATION SYSTEM EXERCISE - LECTURE SHEET (LEVEL - I) (MAIN) (EXERCISE - IV) (Straight Objective & More than one Correct Answer Type Questions)20videos
COMMUNICATION SYSTEM
Similar Questions
A 4μF capacitor is charged by a 200 V supply. It is then disconnected from the supply and is connected to another uncharged 2μF capacitor. How much electrostatic energy of the first capacitor is dissipated in the form of heat and electromagnetic radiation ?
View SolutionA 600pF capacitor is charged by a 200V supply. It is then disconnected from the supply and is connected to another uncharged 600pF capacitor. What is the common potential in V and energy lost in J afrte reconnection?
View SolutionA 600pF capacitor is charged by a 200V supply. It is then disconnected from the supply and is connected to another uncharged 600pF capacitor. What is the common potential in V and energy lost in J after reconnection?
View SolutionA 5μF capacitor is charged fully by a 220 V supply. It is then disconnected from the supply and is connected in series to another uncharged 2.5 μF capacitor . If the energy change during the charge redistribution is X100 J then value of X to the nearest interger is ________.
View SolutionA capacitor C is charged to a potential V by a battery. It is then disconnected from the battery and again connected with its polarity reversed to the battery
View SolutionA capacitor of 60 pF charged to 20 volt. Now battery is removed and then this capacitor is connected to another identical uncharged capacitor. Find heat loss in nJ
View SolutionA capacitor of 60 pF charged to 20 volt. Now battery is removed and then this capacitor is connected to another identical uncharged capacitor. Find heat loss in nJ
View SolutionThe charge on the 4μF capacitor in the steady state is
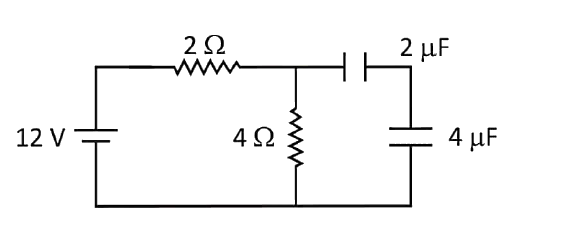 View Solution
View SolutionA capacitor of capacitance value 1μF is charged to 30 V and the battery is then disconnected. If it is connected across a 2μF capacotor, then the energy lost by the system is
View SolutionFind the charges on 6μF and 4μF capacitors
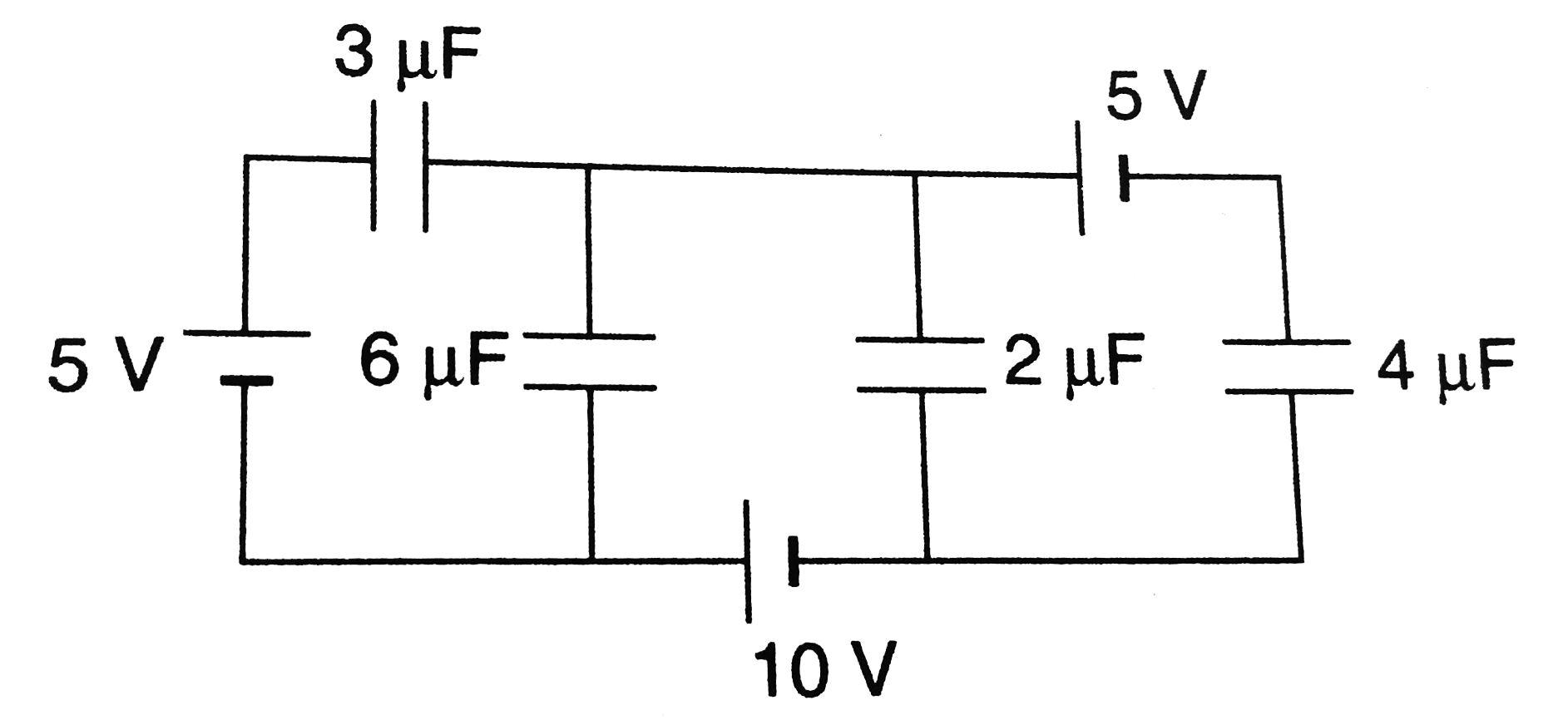 View Solution
View Solution

