A 5μF capacitor is charged fully by a 220 V supply. It is then disconnected from the supply and is connected in series to another uncharged 2.5 μF capacitor . If the energy change during the charge redistribution is X100 J then value of X to the nearest interger is ________.
To solve the problem, we need to follow these steps:
Step 1: Calculate the initial charge on the 5 µF capacitor
The charge Q0 on a capacitor is given by the formula:
Q0=C⋅V
where C is the capacitance and V is the voltage.
Given:
- C=5μF=5×10−6F
- V=220V
Calculating Q0:
Q0=5×10−6F⋅220V=1.1×10−3C
Step 2: Determine the equivalent capacitance when connected in series with the uncharged capacitor
When two capacitors are connected in series, the equivalent capacitance Ceq is given by:
1Ceq=1C1+1C2
For our case:
- C1=5μF=5×10−6F
- C2=2.5μF=2.5×10−6F
Calculating Ceq:
1Ceq=15×10−6+12.5×10−6=210−6+410−6=610−6
Ceq=10−66=53μF
Step 3: Calculate the final charge on the equivalent capacitance
Since the total charge Q0 is conserved, the final charge Qf on the equivalent capacitance is:
Qf=Q0=1.1×10−3C
Step 4: Calculate the initial and final energy stored in the capacitors
The energy stored in a capacitor is given by:
E=Q22C
Initial energy Ei in the 5 µF capacitor:
Ei=Q202C1=(1.1×10−3)22×5×10−6=1.21×10−61×10−5=0.121J
Final energy Ef in the equivalent capacitance:
Ef=Q2f2Ceq=(1.1×10−3)22⋅53×10−6=1.21×10−6103×10−6=1.21×310=0.363J
Step 5: Calculate the change in energy
The change in energy ΔE is given by:
ΔE=Ei−Ef=0.121J−0.363J=−0.242J
Step 6: Relate the change in energy to the given expression
According to the problem, the energy change is given as X100J:
−0.242=X100
Multiplying both sides by 100:
X=−24.2
Since we are asked for the nearest integer value of X:
X≈−24
Final Answer
The value of X to the nearest integer is -24.
---
The charge Q0 on a capacitor is given by the formula:
Q0=C⋅V
where C is the capacitance and V is the voltage.
- C=5μF=5×10−6F
- V=220V
Q0=5×10−6F⋅220V=1.1×10−3C
When two capacitors are connected in series, the equivalent capacitance Ceq is given by:
1Ceq=1C1+1C2
- C1=5μF=5×10−6F
- C2=2.5μF=2.5×10−6F
1Ceq=15×10−6+12.5×10−6=210−6+410−6=610−6
Ceq=10−66=53μF
Since the total charge Q0 is conserved, the final charge Qf on the equivalent capacitance is:
Qf=Q0=1.1×10−3C
The energy stored in a capacitor is given by:
E=Q22C
Ei=Q202C1=(1.1×10−3)22×5×10−6=1.21×10−61×10−5=0.121J
Ef=Q2f2Ceq=(1.1×10−3)22⋅53×10−6=1.21×10−6103×10−6=1.21×310=0.363J
The change in energy ΔE is given by:
ΔE=Ei−Ef=0.121J−0.363J=−0.242J
According to the problem, the energy change is given as X100J:
−0.242=X100
Multiplying both sides by 100:
X=−24.2
X≈−24
The value of X to the nearest integer is -24.
Topper's Solved these Questions
Similar Questions
A 4μF capacitor is charged by a 200 V battery. It is then disconnected from the supply and is connected to another uncharged 2μF capacitor. During the process loss of energy (in J) s
View SolutionA 600pF capacitor is charged by a 200V supply. It is then disconnected from the supply and is connected to another uncharged 600pF capacitor. What is the common potential in V and energy lost in J afrte reconnection?
View SolutionA 600pF capacitor is charged by a 200V supply. It is then disconnected from the supply and is connected to another uncharged 600pF capacitor. What is the common potential in V and energy lost in J after reconnection?
View SolutionA 4μF capacitor is charged by a 200 V supply. It is then disconnected from the supply and is connected to another uncharged 2μF capacitor. How much electrostatic energy of the first capacitor is dissipated in the form of heat and electromagnetic radiation ?
View SolutionThe charge in the 2μF capacitor at steady state is
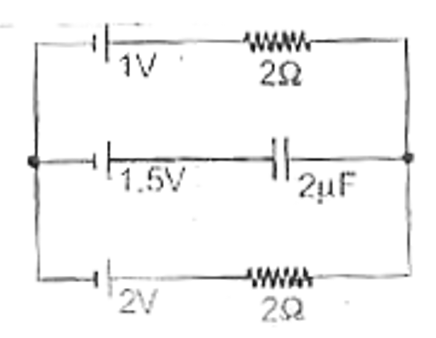
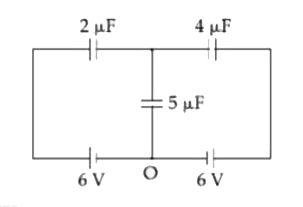
View SolutionIn the circuit shown , charge on the 5μF capacitor is :
View SolutionA capacitor of capacity 2μF is charged to 100V. What is the heat generated when this capacitor is connected in parallel to an another capacitor of same capacity?
View SolutionA capacitor C is fully charged with voltage V0. After disconnecting the voltage source, it is connected in parallel with another uncharged capacitor of capacitance C2. The energy loss in the process after the charge is distributed between the two capacitors is :
View SolutionA 1.5μf capacitor is charged to 20 V. The charging battery is then disconnected and a 15 mH coil is connected in series with the capacitance so that LC oscillations occur. Write current in the inductor as a function of time
View SolutionIn given circuit, ratio of charge on 2 μF capacitor to the charge of 3 μ F capacitor will be
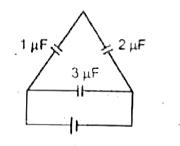
View Solution
