In a YDSE, the central beight fringe can be indentified:
as it has greater intensity than the other bright fringes
as it is wider than the other bright fringes
as it is narrower than the other bright fringes
by using white light instead of single wave- length light .
The correct Answer is:D
Step by step video & image solution for In a YDSE, the central beight fringe can be indentified: by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - LECTURE SHEET EXERCISE-I (LEVEL -II) (ADVANCED ) More than one correct answer Type Questions4videos
WAVE OPTICS
- BOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - LECTURE SHEET EXERCISE-I (LEVEL -II) (ADVANCED ) Linked Comprehension Type Questions7videos
WAVE OPTICS
- BOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - LECTURE SHEET EXERCISE-I (LEVEL -I) (MAIN) straight objective Type Questions16videos
WAVE OPTICS
- BOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - PROBLEMS (LEVEL - II)97videos
WAVE MOTION AND SOUND
- BOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-III (Doppler effect :)15videos
WAVES
Similar Questions
In Young's interference experiment, the central bright fringe can be indentified due to the fact that it
View SolutionStatement-1: if white light is used in YDSE, then the central bright fringe will be white.
Statement-2: In case of white light used in YDSE all the wavelengths produce their zero order maxima at the same position.View Solution
Knowledge Check
- Question 1 - Select One
Assertion : The fringe closest on either side of the central white fringe in case of interference pattern due to white light is red and the farthest appears blue.
Reason : The interference patterns due to different component colours of white light overlap.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf both assertion and reason are false.
In YDSE, having slits of equal width, let β be the fringe width and I0 be the maximum intensity. At a distance x from the central brigth fringe, the intensity will be
View SolutionRed light I(λ=664nm in vacuum) is used in Young's experiment with the slits separated by a distance from the screen given by D=2.75m. Find the distance y on the screen between the central bright fringe and the third-order bright fringe.
Reasoning: This problem can be solved by the first using Eq. (i) to determine the value of θ that locates the third-order bright fringe. Then, trigonometry can be used to obatin the distance y.View SolutionAssertion (A) : In YDSE, as shown in figure, central bright frings is formed at O If a liquid is filled between plane of slits and screen the central bright fringes is shifted in upward direction.
Reasoning (R ) : Path difference at O will increase, so y-coordinate will increase.
View SolutionA monochromatic beam of light fall on YDSE apparatus at some angle (say θ) as shown in figure. A thin sheet of glass is inserted in front of the lower slit s2. The central bright fringe (path difference =0) will be obtained
View SolutionA monochromatic beam of light fall on YDSE apparatus at some angle (say θ) as shown in figure. A thin sheet of glass is inserted in front of the lower slit s2. The central bright fringe (path difference =0) will be obtained
View SolutionA monochromatic beam of light fall on YDSE apparatus at some angle (say θ) as shown in figure. A thin sheet of glass is inserted in front of the lower slit s2. The central bright fringe (path difference =0) will be obtained
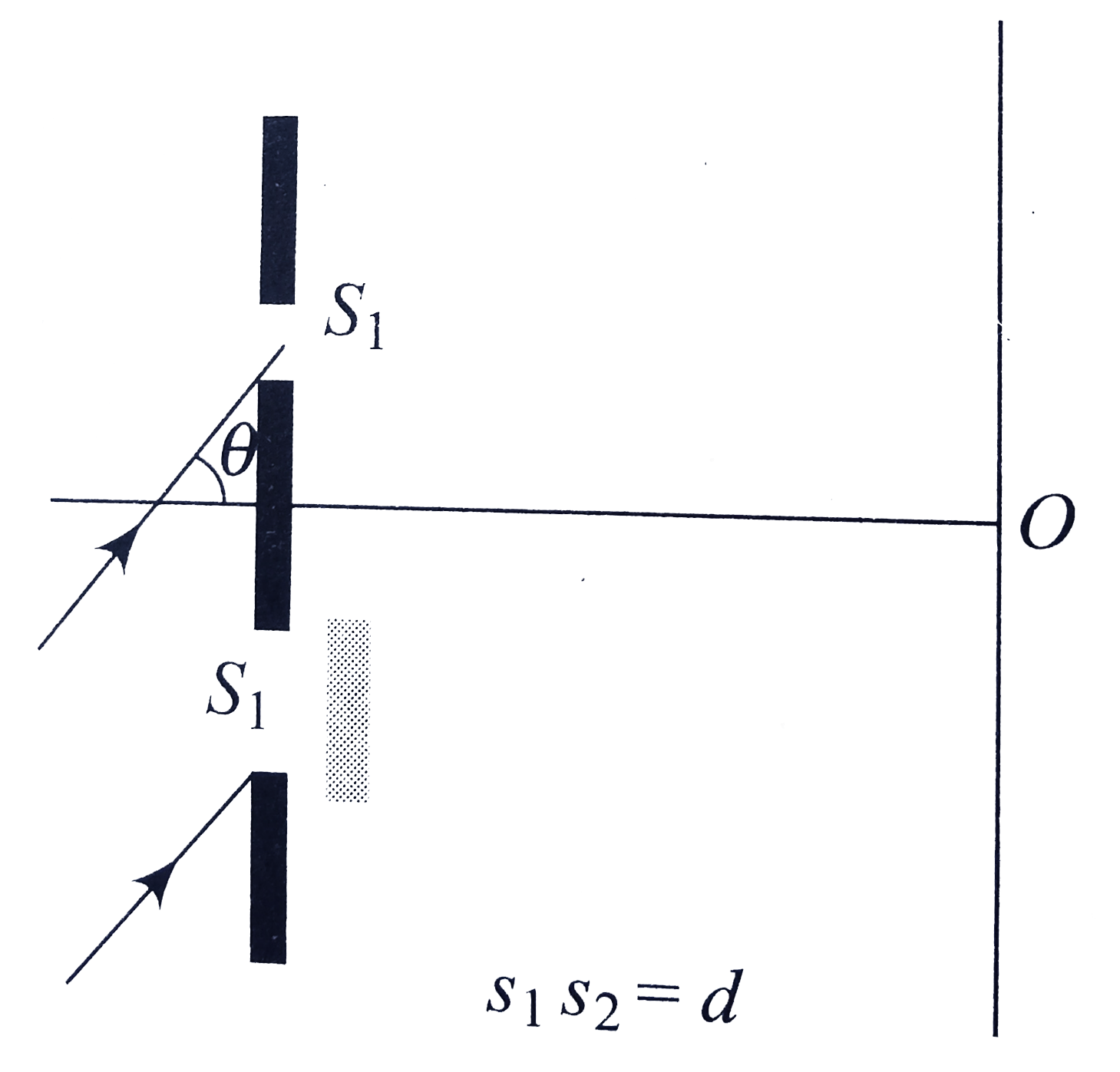View SolutionIn a YDSE, fringes are produced by monochromatic light of wavelength 5450Å. A thin plate of glass of refractive index 1.5 is placed normally in the path of one of the intefering beams and the central bright band of the fringe system is found to move into the position previoysly occupied by the third band from the centre. select the correct alternatie
View Solution