A copper strip is introduced in the left gap and a resistance R−0.4Ω is placed in the right gap of a meter bridge experiment. The balance points before and after interchanging the copper strip and the resistance R are 30 cm and 60 cm respectively. The resistance per unit length of the bridge wire is
4Ω.m−1
3Ωm−1
34Ωm−1
43Ωm−1
The correct Answer is:D
To solve the problem regarding the meter bridge experiment with a copper strip and a resistance R=0.4Ω, we need to analyze the balance points before and after interchanging the copper strip and the resistance.
1. Understanding the Meter Bridge Setup:
In a meter bridge, the balance point L is given by the formula:
R1R2=L1L2
where R1 is the resistance in one gap and R2 is the resistance in the other gap, and L1 and L2 are the lengths from the ends of the bridge wire to the balance point.
2. Identifying the Given Values:
- When the copper strip is in the left gap, the balance point is at 30cm.
- When the copper strip is interchanged with the resistance R, the balance point shifts to 60cm.
- The resistance R=0.4Ω.
3. Setting Up the Equations:
- Let the resistance of the copper strip be Rc.
- For the first balance point (copper strip in the left gap):
Rc0.4=3070(since total length is 100 cm)
- Simplifying this gives:
Rc=0.4×3070=0.4×37=1.27≈0.1714Ω
4. For the Second Balance Point:
- Now, when the copper strip is in the right gap:
0.4Rc=6040
- Simplifying this gives:
0.4×4060=Rc⇒Rc=0.4×23=0.83≈0.2667Ω
5. Calculating the Resistance per Unit Length:
- The average resistance of the copper strip from both calculations can be used to find the resistance per unit length of the bridge wire.
- Let r be the resistance per unit length of the wire.
- The total resistance of the bridge wire is 100r.
- The balance point equations can be used to express r:
R_c = r \times L_c \quad \text{(where L_c is the length of the copper strip)}
- Using the average Rc value, we can solve for r.
6. Final Calculation:
- The average Rc from both balance points is:
Rc=0.1714+0.26672≈0.21905Ω
- Assuming the length of the copper strip is Lc=30cm:
r=RcLc=0.219050.30≈0.7302Ω/m
Conclusion:
The resistance per unit length of the bridge wire is approximately 0.7302Ω/m.
In a meter bridge, the balance point L is given by the formula:
R1R2=L1L2
where R1 is the resistance in one gap and R2 is the resistance in the other gap, and L1 and L2 are the lengths from the ends of the bridge wire to the balance point.
- When the copper strip is in the left gap, the balance point is at 30cm.
- When the copper strip is interchanged with the resistance R, the balance point shifts to 60cm.
- The resistance R=0.4Ω.
- Let the resistance of the copper strip be Rc.
- For the first balance point (copper strip in the left gap):
Rc0.4=3070(since total length is 100 cm)
- Simplifying this gives:
Rc=0.4×3070=0.4×37=1.27≈0.1714Ω
- Now, when the copper strip is in the right gap:
0.4Rc=6040
- Simplifying this gives:
0.4×4060=Rc⇒Rc=0.4×23=0.83≈0.2667Ω
- The average resistance of the copper strip from both calculations can be used to find the resistance per unit length of the bridge wire.
- Let r be the resistance per unit length of the wire.
- The total resistance of the bridge wire is 100r.
- The balance point equations can be used to express r:
R_c = r \times L_c \quad \text{(where L_c is the length of the copper strip)}
- Using the average Rc value, we can solve for r.
- The average Rc from both balance points is:
Rc=0.1714+0.26672≈0.21905Ω
- Assuming the length of the copper strip is Lc=30cm:
r=RcLc=0.219050.30≈0.7302Ω/m
The resistance per unit length of the bridge wire is approximately 0.7302Ω/m.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - PRACTICAL PHYSICSEXERCISE - LECTURE SHEET LEVEL-II (ADVANCED) Straight Objective Type Questions19videos
PRACTICAL PHYSICS
- BOOK - AAKASH SERIESCHAPTER - PRACTICAL PHYSICSEXERCISE - LECTURE SHEET LEVEL-II (ADVANCED) Linked Comprehension Type Questions4videos
PRACTICAL PHYSICS
- BOOK - AAKASH SERIESCHAPTER - PHYSICAL WORLDEXERCISE - Exercise -I10videos
PHYSICAL WORLD
- BOOK - AAKASH SERIESCHAPTER - RAY OPTICSEXERCISE - PROBLEMS ( LEVEL-II)60videos
RAY OPTICS
Similar Questions
Resistance in the two gaps of a meter bridge are 10ohm and 30ohm respectively. If the resistances are interchanged he balance point shifts by
View SolutionWhen un known resistance and a resistance of 4Ω are used in the left and right gaps of a meter bridge, the balance point is 50cm. the shift in the balance point if a 4Ω resistance is now connected parallel to the resistor in right gap ______
View Solution
Knowledge Check
- Question 1 - Select One
In a meter bridge experiment the ratio of left gap resistance to right gap resistance is 2:3 the balance point from is
A60cmB50cmC40cmD20cm - Question 2 - Select One
A wire connected in the left gap of a meter bridge balance a 10Ω resistance in the right gap to a point, which divides the bridge wire in the ratio 3:2. If the length of the wire is 1m. The length of one ohm wire is
A0.057mB0.067mC0.37mD0.134m
In a meter bridge experment, the value of unknown resistance is 2Ω. To get tehbalancing point at 40 cm distance form the same end, the resistance in the resistance box will be :
View SolutionA 6Ω resistance is connected in the left gap of a meter bridge. In the second gap 3Ω and 6Ω are joined in parallel. The balance point of the bridge is at _______
View SolutionIn a metre bridge when the resistance in the left gap is 2Ω and an unknown resistance in the right gap, the balance point is obtained at 40 cm from the zero end. On shunting the unknown resistance with 2Ω find the shift of the balance point on the bridge wire.
View SolutionIf in a meter bridge experiment, the balancing length l was 25 cm for the situation shown in the figure. If the length and diameter of the of wire of resistance R is made half, then find the new balancing length in centimetre is
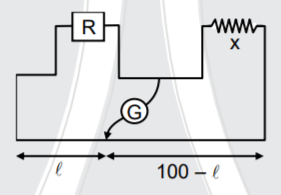 View Solution
View SolutionIf in a meter bridge experiment, the balancing length l was 25 cm for the situation shown in the figure. If the length and diameter of the of wire of resistance R is made half, then find the new balancing length in centimetre is
 View Solution
View SolutionIn a metere bridge, the balance length from left end (standard resistance of 1Ω is in theright gap) is found to be 20cm the length of Resistance in left gap is 12m and radiusis 2mm its specific resistance is
View Solution

