If a straight conductor of length 40cm bent in the form of a square and the current 2A is allowed to pass through square, then find the magnetic induction at the centre of the square loop
To find the magnetic induction at the center of a square loop formed by bending a straight conductor of length 40 cm with a current of 2 A passing through it, we can follow these steps:
1. Determine the Side Length of the Square:
The total length of the conductor is given as 40 cm. Since the conductor is bent into the shape of a square, the length of each side (A) can be calculated as:
4A=40 cm⟹A=40 cm4=10 cm=0.1 m
2. Identify the Geometry:
The center of the square loop is denoted as point O. The distance from the center O to the midpoint of any side of the square is A2.
3. Calculate the Magnetic Field Due to One Side:
The magnetic field induction (B) at the center of the square due to one side of the square can be calculated using the formula for the magnetic field due to a straight conductor:
B=μ0I4πD(sinθ1+sinθ2)
Here, D=A2 and since the angle at the center for each side is 90 degrees, θ1=θ2=45∘.
Thus, we have:
B=μ0I4π(A2)(2sin45∘)
Since sin45∘=1√2, we can simplify this to:
B=μ0I2πA⋅2√2=μ0I√2πA
4. Calculate the Total Magnetic Field:
Since there are 4 sides contributing to the total magnetic field at the center, we multiply the magnetic field due to one side by 4:
Btotal=4⋅μ0I√2πA=4μ0I√2πA
5. Substituting Values:
Now, substituting μ0=4π×10−7T m/A, I=2A, and A=0.1m:
Btotal=4⋅(4π×10−7)⋅2√2⋅π⋅0.1
The π cancels out:
Btotal=8⋅4×10−7√2⋅0.1
6. Calculating the Final Value:
Simplifying further:
Btotal=32×10−70.1√2=32×10−70.1⋅1.414=32×10−70.1414≈2.26×10−5T
Final Answer:
The magnetic induction at the center of the square loop is approximately 2.26×10−5T.
---
The total length of the conductor is given as 40 cm. Since the conductor is bent into the shape of a square, the length of each side (A) can be calculated as:
4A=40 cm⟹A=40 cm4=10 cm=0.1 m
The center of the square loop is denoted as point O. The distance from the center O to the midpoint of any side of the square is A2.
The magnetic field induction (B) at the center of the square due to one side of the square can be calculated using the formula for the magnetic field due to a straight conductor:
B=μ0I4πD(sinθ1+sinθ2)
Here, D=A2 and since the angle at the center for each side is 90 degrees, θ1=θ2=45∘.
B=μ0I4π(A2)(2sin45∘)
Since sin45∘=1√2, we can simplify this to:
B=μ0I2πA⋅2√2=μ0I√2πA
Since there are 4 sides contributing to the total magnetic field at the center, we multiply the magnetic field due to one side by 4:
Btotal=4⋅μ0I√2πA=4μ0I√2πA
Now, substituting μ0=4π×10−7T m/A, I=2A, and A=0.1m:
Btotal=4⋅(4π×10−7)⋅2√2⋅π⋅0.1
The π cancels out:
Btotal=8⋅4×10−7√2⋅0.1
Simplifying further:
Btotal=32×10−70.1√2=32×10−70.1⋅1.414=32×10−70.1414≈2.26×10−5T
The magnetic induction at the center of the square loop is approximately 2.26×10−5T.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IA142videos
MOVING CHARGES AND MAGNETISM
- BOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IB71videos
MOVING CHARGES AND MAGNETISM
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question15videos
MOTION IN A STRAIGHT LINE
- BOOK - AAKASH SERIESCHAPTER - NUCLEAR PHYSICSEXERCISE - ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED) Integer Type Questions3videos
NUCLEAR PHYSICS
Similar Questions
A current of2⋅00A exists in a square loop of edge 10⋅0cm. Find the magnetic field B at the centre of the square loop.
View SolutionA current carrying conductor of length l is bent into two loops one by one. First loop has one turn of wire and the second loop has two turns of wire. Compare the magnetic fields at the centre of the loops
View Solution
Knowledge Check
- Question 1 - Select One
Current flows through uniform square frames as shown. In which case is the magnetic field at the centre of the frame not zero ?
A B
B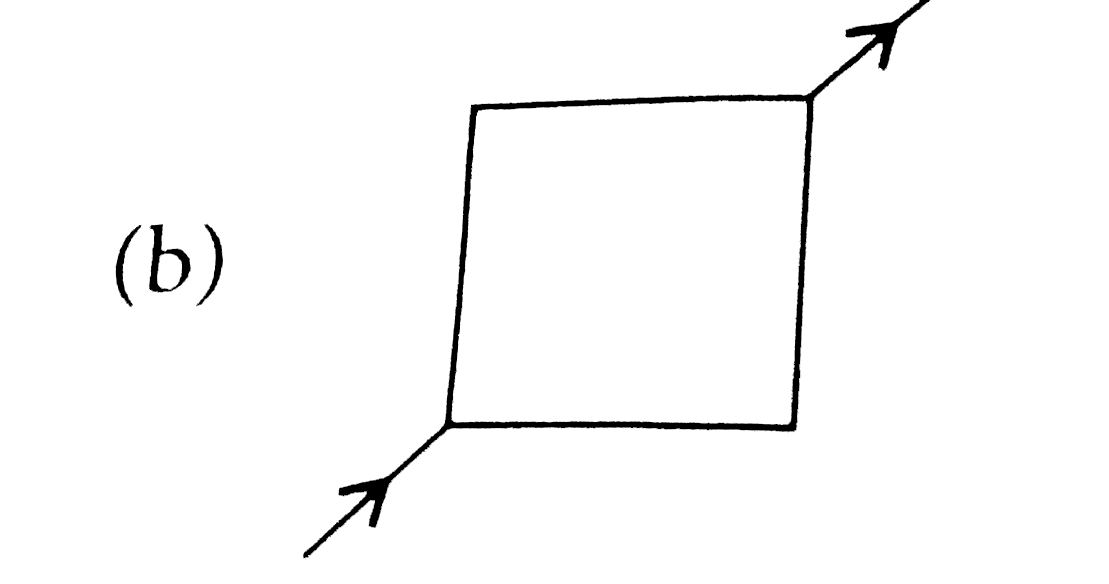 C
C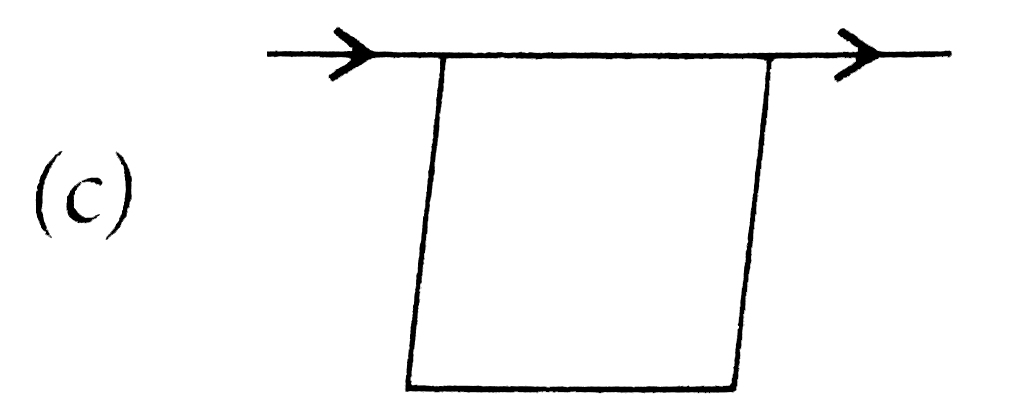 D
D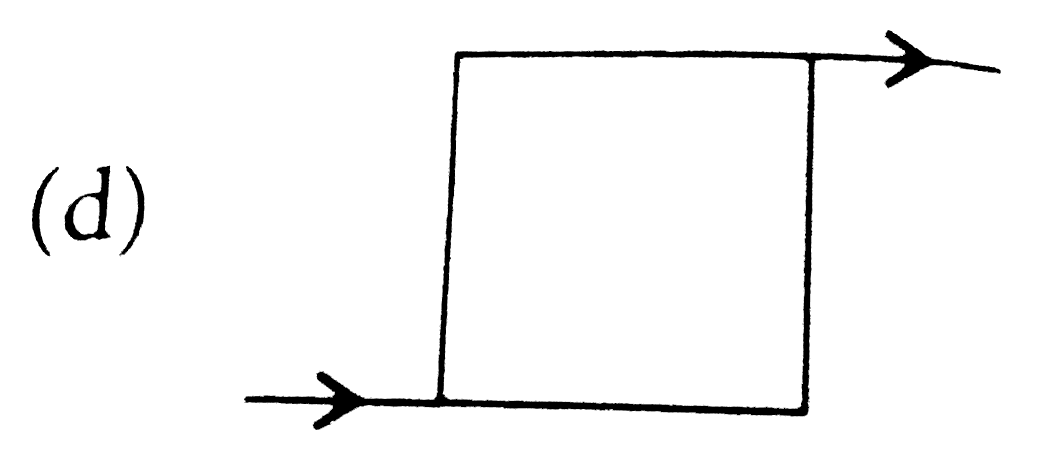
- Question 2 - Select One
Current flows through uniform square frames as shown. In which case is the magnetic field at the centre of the frame not zero ?
A B
B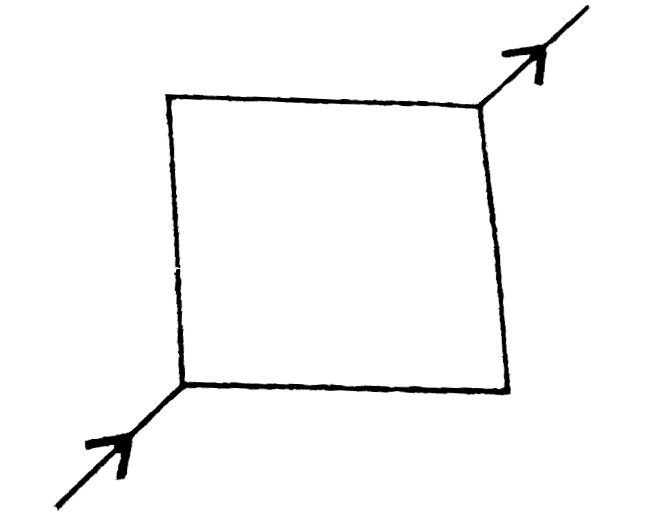 C
C D
D
A current carrying conductor of length l is bent into two loops one by one. First loop has one turn of wire and the second loop has two turns of wire. Compare the magnetic fields at the centre of the loops
View SolutionA square loop of side a carris a current I. The magnetic field at the centre of the loop is
View SolutionA wire of length l is bent in the form of an equilateral triangle and carries an electric current i. (a) Find the magnetic field B at the centre. (b) If the wire is bent in the form of a square, what would be the value of B at the centre?
View SolutionFind magnetic field at centre P if length of side of square loop is 20 cm.
 View Solution
View SolutionA square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is
View Solutiona. A conductor in the shape of a square of edge length l=0.4m carries a current i=10.0A. Calculate the magnitude and direction of magnetic field at the centre of the square.
b. If this conductor is formed into a single circular turn and carries the same current. what is the value of the magnetic field at the centre.
 View Solution
View Solution

