A current carrying conductor of length l is bent into two loops one by one. First loop has one turn of wire and the second loop has two turns of wire. Compare the magnetic fields at the centre of the loops
B'=4B
4B'=B
2B'=B
B'=2B
The correct Answer is:A
To solve the problem of comparing the magnetic fields at the center of two loops formed by a current-carrying conductor, we can follow these steps:
Step 1: Define the parameters
Let:
- L = Length of the conductor
- I = Current flowing through the conductor
- r1 = Radius of the first loop (1 turn)
- r2 = Radius of the second loop (2 turns)
Step 2: Calculate the radius of the loops
For the first loop with one turn:
L=2πr1⟹r1=L2π
For the second loop with two turns:
L=2×2πr2⟹L=4πr2⟹r2=L4π
Step 3: Calculate the magnetic field at the center of the first loop
The magnetic field B at the center of a single loop is given by:
B=μ0I2r
For the first loop:
B1=μ0I2r1=μ0I2(L2π)=μ0I⋅πL
Step 4: Calculate the magnetic field at the center of the second loop
For the second loop with two turns, the magnetic field B′ at the center is:
B′=μ0I⋅n2r
where n is the number of turns. For the second loop:
B′=μ0I⋅22r2=μ0Ir2=μ0I(L4π)=4μ0I⋅πL
Step 5: Compare the magnetic fields
Now we can compare B1 and B′:
B1B′=μ0I⋅πL4μ0I⋅πL=14
Thus,
B′=4B1
Conclusion
The magnetic field at the center of the second loop (with two turns) is four times greater than the magnetic field at the center of the first loop (with one turn).
Let:
- L = Length of the conductor
- I = Current flowing through the conductor
- r1 = Radius of the first loop (1 turn)
- r2 = Radius of the second loop (2 turns)
For the first loop with one turn:
L=2πr1⟹r1=L2π
L=2×2πr2⟹L=4πr2⟹r2=L4π
The magnetic field B at the center of a single loop is given by:
B=μ0I2r
For the first loop:
B1=μ0I2r1=μ0I2(L2π)=μ0I⋅πL
For the second loop with two turns, the magnetic field B′ at the center is:
B′=μ0I⋅n2r
where n is the number of turns. For the second loop:
B′=μ0I⋅22r2=μ0Ir2=μ0I(L4π)=4μ0I⋅πL
Now we can compare B1 and B′:
B1B′=μ0I⋅πL4μ0I⋅πL=14
Thus,
B′=4B1
The magnetic field at the center of the second loop (with two turns) is four times greater than the magnetic field at the center of the first loop (with one turn).
Topper's Solved these Questions
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Assertion and reason
20 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Match the following
4 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Check point
54 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Subjective
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Video
Similar Questions
A square loop of side a carris a current I. The magnetic field at the centre of the loop is
View SolutionA square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is
View SolutionA rectangular loop of metallic wire is of length a and breadth b and carries a current i. The magnetic field at the centre of the loop is
View SolutionThe wire loop shown in figure carries a current as shown. The magnetic field at the centre O is ,

View SolutionA current I flows along a triangle loop having sides of equal length a. The strength of magnetic field at the centre of the loop is :
View SolutionA current I is flowing in a conductor of length L when it is bent in the form of a circular loop its magnetic moment
View SolutionA square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is (dependence on L)
View SolutionA conducting circular loop of radius a is connected to two long, straight wires . The straight wires carry a current I as shown in figure . Find the magnetic field B at the centre of the loop.

View SolutionOne of the two identical conducting wires of length L is bent in the form of a circular loop and the other one into a circular coil of N identical turns. If the same current passed in both, the ratio of the magnetic field at the central of the loop (BL) to that at the central of the coil (BC), i.e. BLBC will be :
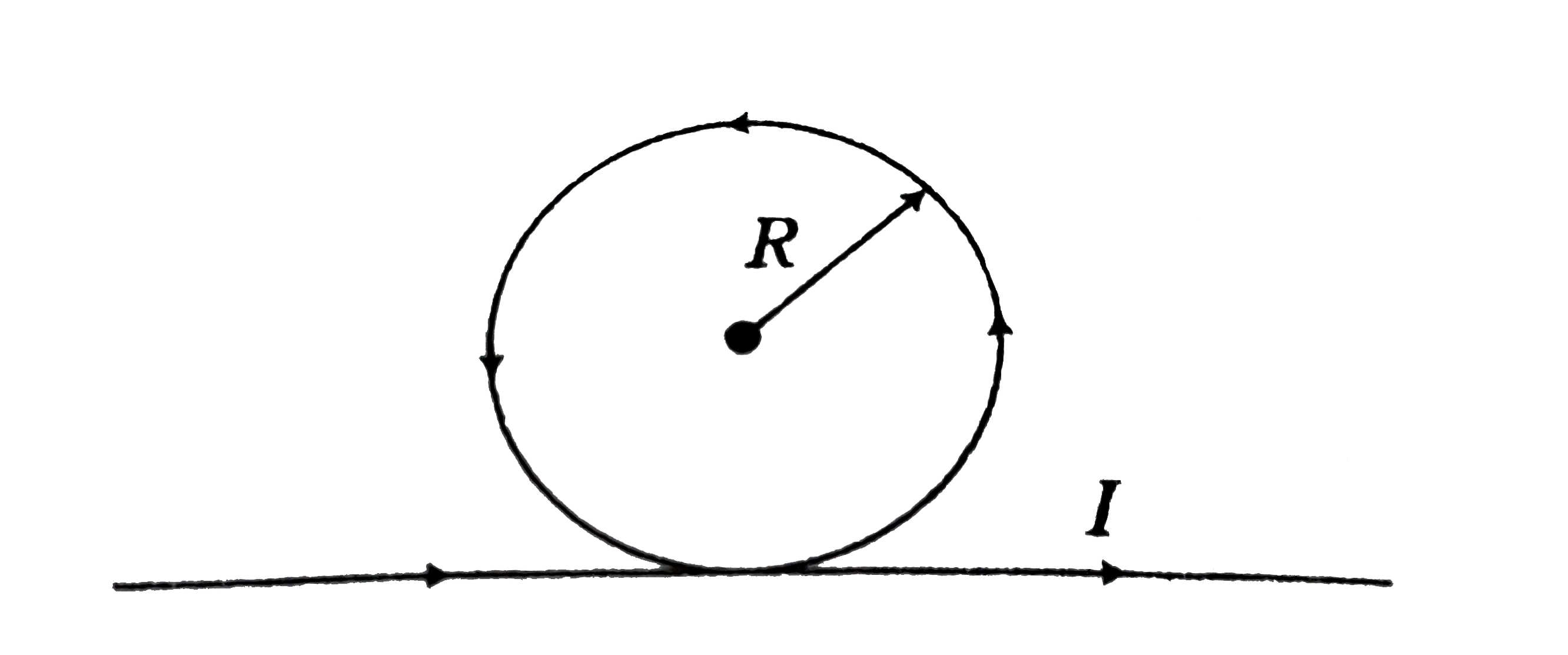
View SolutionAn infinitely long conductor is bent into a circle as shown in figure. It carries a current I ampere and the radius of loop is R metre. The magnetic induction at the centre of loop is
View Solution