An electron moving horizontally from left to right in a region where a magnetic field exists vertically downwards describes: (when seen from above)
horizontal clock-wise circular path
horizontal anti clock-wise circular path
vertical clock-wise circular path
vertical anti clock-wise circular path
The correct Answer is:A
To solve the problem of an electron moving horizontally from left to right in a vertically downward magnetic field, we can follow these steps:
1. Identify the Directions:
- The electron is moving from left to right, which we can denote as the positive x-direction (x̂).
- The magnetic field is directed vertically downward, which we can denote as the negative z-direction (-ẑ).
2. Determine the Velocity Vector:
- The velocity vector of the electron can be represented as:
v=v^x
where v is the speed of the electron.
3. Determine the Magnetic Field Vector:
- The magnetic field vector can be represented as:
B=−B^z
where B is the magnitude of the magnetic field.
4. Apply the Lorentz Force Law:
- The force acting on a charged particle in a magnetic field is given by:
F=q(v×B)
where q is the charge of the electron (which is negative).
5. Calculate the Cross Product:
- We need to calculate the cross product v×B:
F=q(v×B)=q(v^x×(−B^z))
- Using the right-hand rule for the cross product:
^x×^z=^y
- Therefore:
F=−qvB^y
6. Direction of the Force:
- Since the charge of the electron is negative, the actual force acting on the electron will be in the opposite direction of the calculated force:
Freal=−(−qvB^y)=qvB^y
- This means the force will act in the positive y-direction (upward).
7. Determine the Motion Path:
- The upward force will cause the electron to move in a circular path in the x-y plane due to the centripetal nature of the magnetic force.
- Since the force is acting in the positive y-direction, the motion will be clockwise when viewed from above.
8. Conclusion:
- The electron will describe a horizontal clockwise circular path.
Final Answer:
The electron moving horizontally from left to right in a region where a magnetic field exists vertically downwards describes a horizontal clockwise circular path.
---
- The electron is moving from left to right, which we can denote as the positive x-direction (x̂).
- The magnetic field is directed vertically downward, which we can denote as the negative z-direction (-ẑ).
- The velocity vector of the electron can be represented as:
v=v^x
where v is the speed of the electron.
- The magnetic field vector can be represented as:
B=−B^z
where B is the magnitude of the magnetic field.
- The force acting on a charged particle in a magnetic field is given by:
F=q(v×B)
where q is the charge of the electron (which is negative).
- We need to calculate the cross product v×B:
F=q(v×B)=q(v^x×(−B^z))
- Using the right-hand rule for the cross product:
^x×^z=^y
- Therefore:
F=−qvB^y
- Since the charge of the electron is negative, the actual force acting on the electron will be in the opposite direction of the calculated force:
Freal=−(−qvB^y)=qvB^y
- This means the force will act in the positive y-direction (upward).
- The upward force will cause the electron to move in a circular path in the x-y plane due to the centripetal nature of the magnetic force.
- Since the force is acting in the positive y-direction, the motion will be clockwise when viewed from above.
- The electron will describe a horizontal clockwise circular path.
The electron moving horizontally from left to right in a region where a magnetic field exists vertically downwards describes a horizontal clockwise circular path.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IB
71 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-II
79 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-III
49 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question
15 Videos
- NUCLEAR PHYSICSBOOK - AAKASH SERIESCHAPTER - NUCLEAR PHYSICSEXERCISE - ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED) Integer Type Questions
3 Videos
Similar Questions
Knowledge Check
On moving from left to right in a period what is the order of acidic character of hydrides ?
ANH3<H2O<HFBHF<H2O<NH3CH2O<HF<NH3DH2O<NH3<HF
On moving from left to right across a period in the periodic table the metallic character
View SolutionA charged particle is kept at rest on a smooth horizontal surface in uniform magnetic field 'B' which is directed vertically downward as shown in the figure.

An observer is moving with constant velocity v towards right. Then with respect to the observer which of the following statements is/are correct :
View SolutionA conducting loop is moving from left to right through a region of uniform magnetic (B) field. Its four positiors are shown belwo. Show the direction of induced current in all four positions.

View SolutionA beam of protons is moving horizontally towards you. As it approaches, it passes through a magnetic field directed downward. The beam deflects-
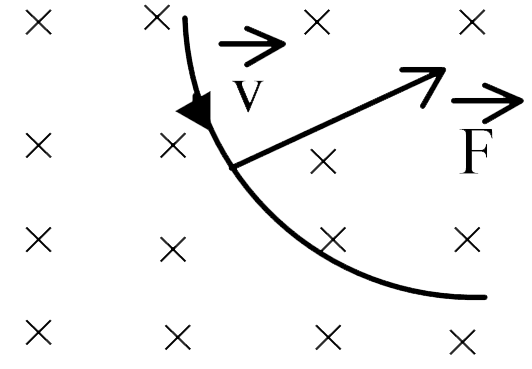
View SolutionA beam consisting of protons and electrons moving at the same speed goes through athin region in which there is a magnetic field perpendicular to the beam. Protons and the electrons
View SolutionA non-conducting rod having circular cross section of radius R is suspended from a rigid support as shown in fig. A light and small coil of 300turns is wrapped tightly at the left end where uniform magnetic filed B exists in vertically downward direction. Air of density ρ hits the half of the right part of the rod with velocity V as shown in the fig. What should be current in clockwise direction (as seen from O) in the coil so that rod remains horizontal? Give answer in mA. Given 2Lv√πRBρ=1√5A−1/2.
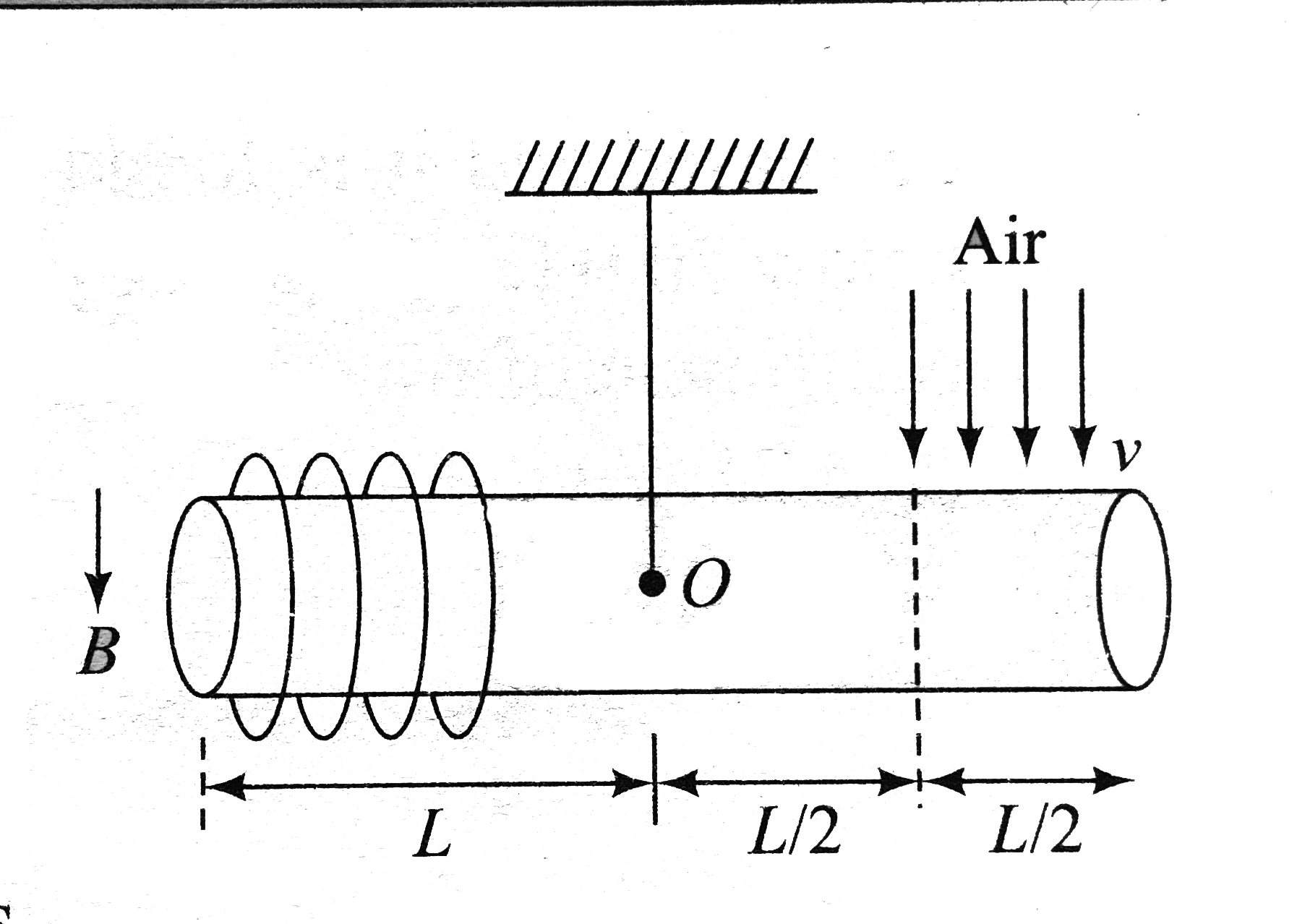
View SolutionAn electron enters a region where magnetic field (B) and electric field (E ) are mutually perpendicular, then
View Solution
