Two condensers of capacities C and 3C are connected in parallel and then connected in series with a third condenser of capacity 3C. The combination is charged with a battery of 'V'volt. The charge on condenser of capacity C is (in coulomb)
1/2(CV)
3CV/7
2CV
3/2(CV)
The correct Answer is:B
To solve the problem step-by-step, we will follow these steps:
Step 1: Determine the Equivalent Capacitance of the Parallel Combination
We have two capacitors, one with capacitance C and the other with capacitance 3C, connected in parallel. The equivalent capacitance C′ for capacitors in parallel is given by:
C′=C+3C=4C
Step 2: Determine the Equivalent Capacitance of the Series Combination
Next, this equivalent capacitor C′=4C is connected in series with a third capacitor of capacitance 3C. The equivalent capacitance C′′ for capacitors in series is given by:
1C′′=1C′+13C
Substituting C′:
1C′′=14C+13C
To combine these fractions, we find a common denominator, which is 12C:
1C′′=312C+412C=712C
Now, taking the reciprocal gives us:
C′′=12C7
Step 3: Calculate the Total Charge in the Circuit
The total charge Q stored in the equivalent capacitor when connected to a battery of voltage V is given by:
Q=C′′⋅V=12C7⋅V=12CV7
Step 4: Determine the Charge on Each Capacitor in Series
In a series circuit, the charge Q on each capacitor is the same. Therefore, the charge on the capacitor with capacitance C (let's denote it as Q1) is given by:
Q1=Q=12CV7
Step 5: Use the Charge Division Rule
Now, we need to find the charge on the capacitor C specifically. The charge on each capacitor in series is proportional to its capacitance. The charge on capacitor C can be expressed as:
Q1=CC+3C⋅Q=C4C⋅12CV7=14⋅12CV7=12CV28=3CV7
Final Answer
Thus, the charge on the capacitor of capacity C is:
Q1=3CV7
We have two capacitors, one with capacitance C and the other with capacitance 3C, connected in parallel. The equivalent capacitance C′ for capacitors in parallel is given by:
Next, this equivalent capacitor C′=4C is connected in series with a third capacitor of capacitance 3C. The equivalent capacitance C′′ for capacitors in series is given by:
The total charge Q stored in the equivalent capacitor when connected to a battery of voltage V is given by:
In a series circuit, the charge Q on each capacitor is the same. Therefore, the charge on the capacitor with capacitance C (let's denote it as Q1) is given by:
Now, we need to find the charge on the capacitor C specifically. The charge on each capacitor in series is proportional to its capacitance. The charge on capacitor C can be expressed as:
Thus, the charge on the capacitor of capacity C is:
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (CUTTENT ELECTRICITY )108videos
APPENDICES ( REVISION EXERCISE )
- BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MOVING CHANGES & MEGNETISM)95videos
APPENDICES ( REVISION EXERCISE )
- BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )52videos
APPENDICES ( REVISION EXERCISE )
- BOOK - AAKASH SERIESCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE - III24videos
ALTERNATING CURRENT
- BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION128videos
APPENDICES (REVISION EXERCISE)
Similar Questions
Two condensers of capacities 4mF and 6mF are connected to two cells as shown. Then
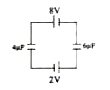 View Solution
View SolutionTwo capacitors 2μFand4μF are connected in parallel. A third capacitor of 6μF capacity is connected in series. The combination is connected across a 12 V battery. The voltage across a 2μF capacitor is
 View Solution
View SolutionA condenser of capacity 1 μ F and a resistance 0.5 mega-ohm are connected in series with a DC supply of 2 V. The time constant of circuit is
View SolutionThree condensers each of capacity C microfarad are connected in series. An exactly similar set is connected in parallel to the first one. The effective capacity of the combination is 4μF. Then, the value of C in microfard is
View SolutionThree condensers of capacities 3 mF, 6 mF, 12mF are connected in series with a battery. If the charge on 12 mF condenser is 24 mC, the P.D. across the battery is
View SolutionThree.condensers of capacity 4mF,2mFand3mF are connected such that 2 mF and 3 mF are in series and 4 mF is parallel to them. The equivalent capacity of the combination is
View SolutionA and B are two points in a closed circuit. The potential difference across the condenser of capacity 5μF is
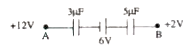 View Solution
View SolutionFigure shows two capacitors of capacitance 2μF and 4μF and a cell of 90 V. The switch 'k' is such that when it is in position 1, the circuit ABCD is closed and when it is in position 2, the circuit BCEF is closed.the resistance of both the circuits is negligible os that the capacitor gets fully charged instantly. Initially the switch is in position1. then it is turned in position 2 and then in position 1. Now two cycles are completed. Find the charge (inμC) after two cycles.
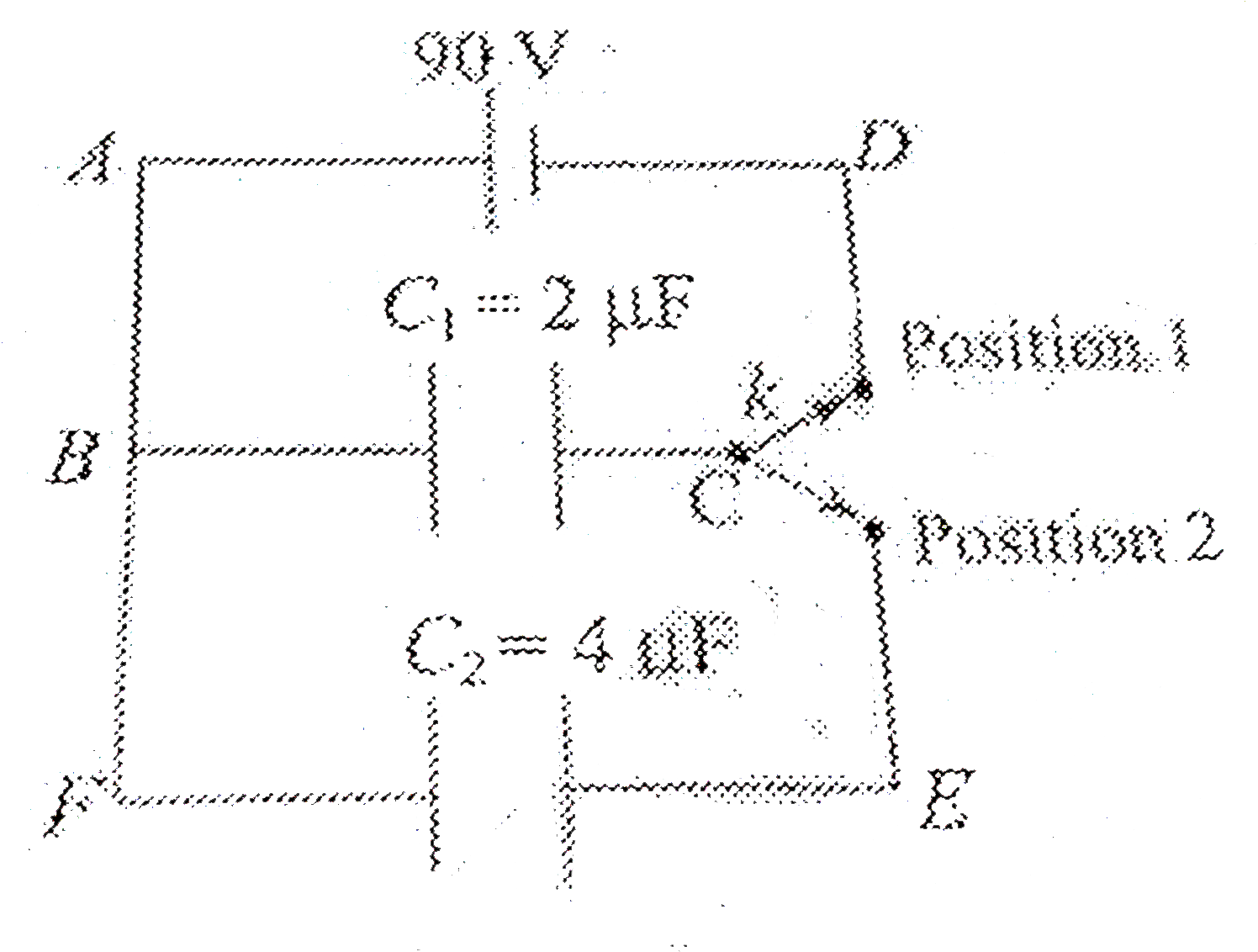 View Solution
View SolutionTwo condensers of capacity 0.3μF and 0.6μF respectively are connected in series. The combination is connected across a potential of 6 volts. The ratio of energies stored by the condensers will be
View SolutionTwo similar condensers are connected in parallel and are charged to a potential V. Now these are separated out and are connected in series. Then
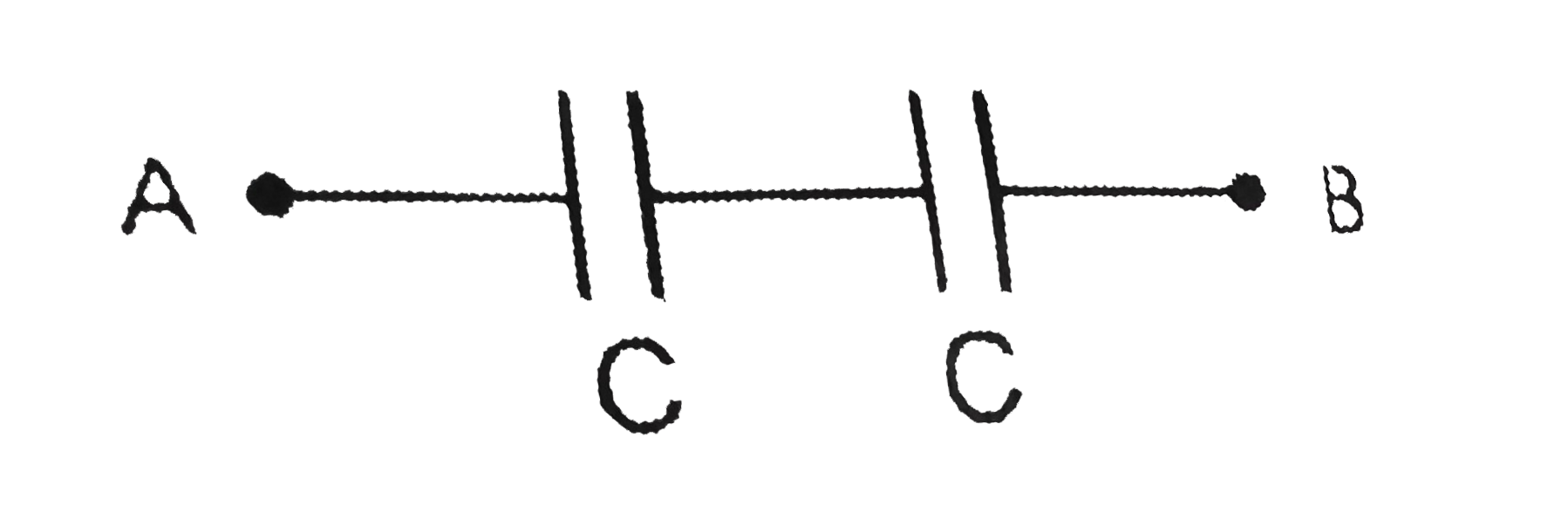 View Solution
View Solution
