A number of capacitors, each of capacitance and each one of which gets punctured if a potential difference just exceeding 500 volt is applied are provided. Then an arrangement suitable for giving a capacitor of capacitance across which 2000 V may be applied requires at least
4 component capacitors
96 component capacitors
48 component capacitors
3 component capacitors
The correct Answer is:C
To solve the problem, we need to determine the minimum number of capacitors required to achieve a capacitance of 3 µF that can withstand a voltage of 2000 V, given that each capacitor has a capacitance of 1 µF and can only handle up to 500 V before puncturing.
1. Identify the maximum voltage per capacitor:
Each capacitor can handle a maximum voltage of 500 V.
2. Determine the total voltage to be applied:
We need to apply a total voltage of 2000 V.
3. Calculate the number of capacitors in series:
To find out how many capacitors we need in series to handle 2000 V:
Vtotal=V0×m
where V0=500V (the maximum voltage per capacitor) and Vtotal=2000V.
Rearranging gives:
m=VtotalV0=2000V500V=4
So, we need 4 capacitors in series.
4. Calculate the equivalent capacitance of capacitors in series:
The formula for the equivalent capacitance Cs of capacitors in series is:
1Cs=1C+1C+1C+1C=4C
Given that each capacitor has a capacitance of C=1μF:
1Cs=41μF⟹Cs=14μF=0.25μF
5. Determine the total capacitance required:
We need a total capacitance of Ctotal=3μF.
6. Calculate the number of series groups needed:
Since the equivalent capacitance of one series group is 0.25μF, we can find the number of such groups n needed in parallel to achieve 3μF:
Ctotal=n×Cs⟹n=CtotalCs=3μF0.25μF=12
So, we need 12 series groups.
7. Calculate the total number of capacitors:
The total number of capacitors N required is given by:
N=m×n=4×12=48
Final Answer:
The minimum number of capacitors required is 48.
Each capacitor can handle a maximum voltage of 500 V.
We need to apply a total voltage of 2000 V.
To find out how many capacitors we need in series to handle 2000 V:
Vtotal=V0×m
where V0=500V (the maximum voltage per capacitor) and Vtotal=2000V.
Rearranging gives:
m=VtotalV0=2000V500V=4
So, we need 4 capacitors in series.
The formula for the equivalent capacitance Cs of capacitors in series is:
1Cs=1C+1C+1C+1C=4C
Given that each capacitor has a capacitance of C=1μF:
1Cs=41μF⟹Cs=14μF=0.25μF
We need a total capacitance of Ctotal=3μF.
Since the equivalent capacitance of one series group is 0.25μF, we can find the number of such groups n needed in parallel to achieve 3μF:
Ctotal=n×Cs⟹n=CtotalCs=3μF0.25μF=12
So, we need 12 series groups.
The total number of capacitors N required is given by:
N=m×n=4×12=48
The minimum number of capacitors required is 48.
Topper's Solved these Questions
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (CUTTENT ELECTRICITY )
108 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MOVING CHANGES & MEGNETISM)
95 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )
52 Videos
- ALTERNATING CURRENTBOOK - AAKASH SERIESCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE - III
24 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
128 Videos
Similar Questions
A number of capacitors each of capacitance 1μF and each one of which get punctured if a potential difference just exceeding 500 volt is applied, are provided. Then an arrangement suitable for giving a capacitor of 2μF across which 3000 volt may be applied requires at least-
View SolutionThree capacitors with capacitances of 1μF,2μFand3μF are connected in series. Each capacitor gets punctured, if a potential difference just exceeding 100 volt is applied. If the group is connected across 220 volt circuit then the capacitor most likely to puncture first is
View Solution
Knowledge Check
The potential difference between points A and B is
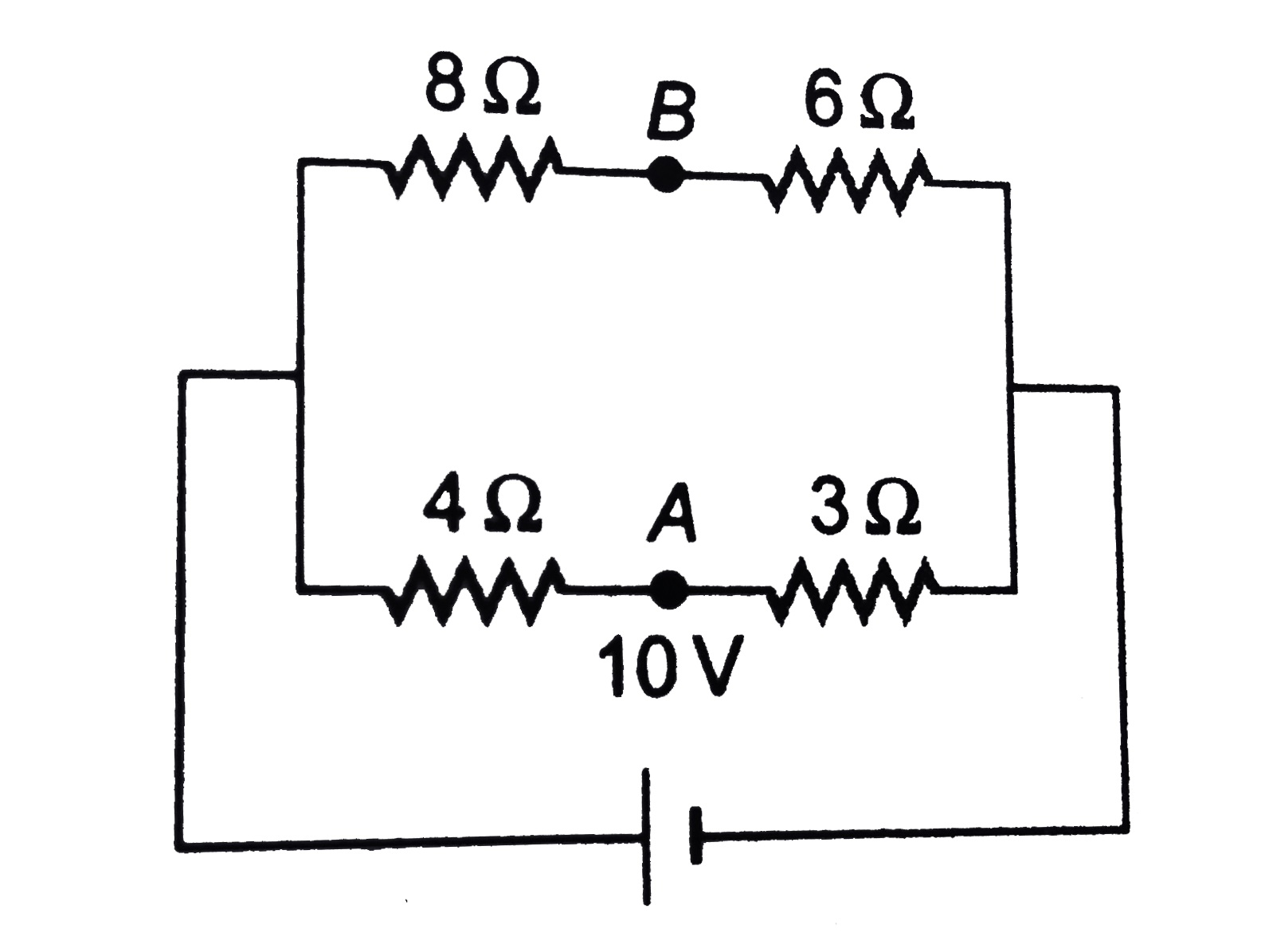 A2B5C11D18
A2B5C11D18
The capacitor of capacitance 4μF and 6μF are connected in series. A potential difference of 500 volts applied to the outer plates of the two capacitor system. Then the charge on each capacitor is numerically
View SolutionSix 1μF capacitors are so arranged that their equivalent capacitance is 0.70μF. If a potential difference of 600 volt is applied to the combination, what charge will appear on each capacitor ?
View SolutionA parallel plate capacitor of capacitance 1μF has a charge of +2μC on one of the plates and a charge of +4μC on the other. The potential difference developed across the capacitor is
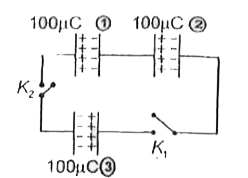
View SolutionThree identical charged capacitors each of capacitance 5 μF are connected as shown in figure. Potential difference across capacitor (3), long time after the swithces K1andK2 are closed , is
View SolutionA capacitor of capacitance 6 μF is connected with an emf sourface 3 V. Electrostaci energy stored in the capacitor is
View SolutionTwo capacitors of capacitances 20.0pF and 50.0pF are connected in series with a 6.00V bettery . Find (a )the potential difference across each capacitor and (b) the energy stored in each capacitor .
View SolutionThree capacitors of capacitances 6μFeach are available.The minimum and maximam capacitances,which be obtained are
View Solution
