Six 1μF capacitors are so arranged that their equivalent capacitance is 0.70μF. If a potential difference of 600 volt is applied to the combination, what charge will appear on each capacitor ?
The correct Answer is:420μC on one, 180μC on two, 60μC on remaining 3 capacitors
To solve the problem step by step, we will analyze the arrangement of the capacitors and apply the relevant formulas for capacitors in series and parallel.
Step 1: Understanding the Arrangement
We have six capacitors, each with a capacitance of 1μF. The equivalent capacitance of the arrangement is given as 0.7μF. We need to determine how these capacitors are arranged to achieve this equivalent capacitance.
Step 2: Finding the Charge on the Combination
Using the formula for charge, we can find the total charge Q on the combination when a potential difference V is applied:
Q=Ceq×V
Where:
- Ceq=0.7μF
- V=600V
Calculating the charge:
Q=0.7×10−6F×600V=420×10−6C=420μC
Step 3: Analyzing the Series and Parallel Configuration
Assuming a configuration where three capacitors are in series and two capacitors are in parallel with this series combination, we can analyze the voltage across each section.
Step 4: Finding Voltage Across Series Capacitors
In a series configuration, the charge is the same across all capacitors. Therefore, the charge on the three capacitors in series is Q=420μC.
To find the voltage across these three capacitors, we use:
Vseries=QCseries
Where Cseries for three capacitors in series is:
1Cseries=1C+1C+1C=3C⟹Cseries=C3=1μF3=13μF
Calculating the voltage across the series capacitors:
Vseries=420μC13μF=420×3=1260V
Step 5: Finding Voltage Across Parallel Capacitors
Since the total voltage is 600V, the voltage across the three capacitors in series is Vseries=420V. The remaining voltage across the two parallel capacitors is:
Vparallel=600V−420V=180V
Step 6: Finding Charge on Each Parallel Capacitor
The charge on each of the two capacitors in parallel is given by:
Qparallel=C×Vparallel=1μF×180V=180μC
Step 7: Finding Charge on Each Series Capacitor
The charge on the three capacitors in series is the same:
Qseries=420μC
Final Summary of Charges
- Charge on each of the three capacitors in series: 420μC
- Charge on each of the two capacitors in parallel: 180μC
Conclusion
The charges on the capacitors are:
- Three capacitors in series: 420μC each
- Two capacitors in parallel: 180μC each
We have six capacitors, each with a capacitance of 1μF. The equivalent capacitance of the arrangement is given as 0.7μF. We need to determine how these capacitors are arranged to achieve this equivalent capacitance.
Using the formula for charge, we can find the total charge Q on the combination when a potential difference V is applied:
- Ceq=0.7μF
- V=600V
Assuming a configuration where three capacitors are in series and two capacitors are in parallel with this series combination, we can analyze the voltage across each section.
In a series configuration, the charge is the same across all capacitors. Therefore, the charge on the three capacitors in series is Q=420μC.
Since the total voltage is 600V, the voltage across the three capacitors in series is Vseries=420V. The remaining voltage across the two parallel capacitors is:
The charge on each of the two capacitors in parallel is given by:
The charge on the three capacitors in series is the same:
- Charge on each of the three capacitors in series: 420μC
- Charge on each of the two capacitors in parallel: 180μC
The charges on the capacitors are:
- Three capacitors in series: 420μC each
- Two capacitors in parallel: 180μC each
Topper's Solved these Questions
- CAPACITANCEBook:RESONANCE ENGLISHChapter:CAPACITANCEExercise:Exercise - 3
Explore 26 Videos
- ATOMIC PHYSICSBook:RESONANCE ENGLISHChapter:ATOMIC PHYSICSExercise:Advanved level problems
Explore 17 Videos
- COMMUNICATION SYSTEMSBook:RESONANCE ENGLISHChapter:COMMUNICATION SYSTEMSExercise:Exercise 3
Explore 13 Videos
Similar Questions
The capacitor of capacitance 4μF and 6μF are connected in series. A potential difference of 500 volts applied to the outer plates of the two capacitor system. Then the charge on each capacitor is numerically
View SolutionA capacitor when charged by a potential difference of 200 Volts, stores a charge of 0.1C. By discharging energy liberated by the capacitor is-
View SolutionIn the circuit shown , charge on the 5μF capacitor is :
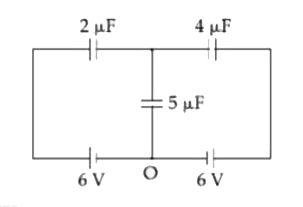
View SolutionA capacitor of 10(μ)F and an inductor of 1 H are joined in series. An ac of 50 Hz is applied to this combination. What is the impedance of the combination?
View SolutionA number of capacitors each of capacitance 1μF and each one of which get punctured if a potential difference just exceeding 500 volt is applied, are provided. Then an arrangement suitable for giving a capacitor of 2μF across which 3000 volt may be applied requires at least-
View SolutionWhile working on a physics project at school physics, lab, you require a 4 μF capacitor in a circuit across a potential difference of 1 k V. Unfortunately, 4 μF capacitors are out or stock in your lab but 2 μF capacitors which can withstand a potential difference of 400 V are available in plenty . if you decide to use the 2 μF capacitors in place of 4μ F capacitor minimum number of capacitors required are
View SolutionA network of four 10μF capacitors is connected to a 500 V supply, as shown in Fig. Determine (a) the equivalent capacitance of the network and (b) the charge on each capacitor. (Note, the charge on a capacitor is the charge on the plate with higher potential, equal and opposite to the charge on the plate with lower potential.)

View SolutionIn the given circuit, the charge on 4μF capacitor will be :

View SolutionAn electrical technician requires a capacitance of 2μF in a circuit across a potential difference of 1 kV. A large number of 1μF capacitors are available to him each of which can withstand a potential difference of not more than 400 V. Suggest a possible arrangement that requires the minimum number of capacitors.
View SolutionThree capacitors each of capacitance 9 pF are connected in series. What is the total capacitance of the combination ?
View Solution
