A condenser of capacity 2mF charges to a potential 200V is connected in parallel with a condenser of same capacity but charged to a potential 100V. The percentage loss of energy of system is
50%
35%
20%
10%
The correct Answer is:D
To solve the problem, we need to calculate the initial energy stored in each capacitor, the total energy before they are connected, the energy after they are connected, and finally the percentage loss of energy.
1. Identify the given values:
- Capacitor 1 (C1) = 2 mF = 2 x 10^-3 F
- Voltage across C1 (V1) = 200 V
- Capacitor 2 (C2) = 2 mF = 2 x 10^-3 F
- Voltage across C2 (V2) = 100 V
2. Calculate the energy stored in C1 (U1):
U1=12C1V12
U1=12×2×10−3×(200)2
U1=12×2×10−3×40000
U1=40 joules
3. Calculate the energy stored in C2 (U2):
U2=12C2V22
U2=12×2×10−3×(100)2
U2=12×2×10−3×10000
U2=10 joules
4. Calculate the total initial energy (U):
U=U1+U2=40+10=50 joules
5. Calculate the total charge before connecting the capacitors:
- Charge on C1 (Q1):
Q1=C1×V1=2×10−3×200=0.4 coulombs
- Charge on C2 (Q2):
Q2=C2×V2=2×10−3×100=0.2 coulombs
- Total charge (Q):
Q=Q1+Q2=0.4+0.2=0.6 coulombs
6. Calculate the equivalent capacitance (Ceq):
Ceq=C1+C2=2×10−3+2×10−3=4×10−3 F
7. Calculate the energy stored in the equivalent capacitor (U'):
U′=12Q2Ceq
U′=12(0.6)24×10−3
U′=120.364×10−3=0.368×10−3=45 joules
8. Calculate the loss of energy:
Loss of energy=U−U′=50−45=5 joules
9. Calculate the percentage loss of energy:
Percentage loss=(Loss of energyU)×100
Percentage loss=(550)×100=10%
Final Answer:
The percentage loss of energy of the system is 10%.
- Capacitor 1 (C1) = 2 mF = 2 x 10^-3 F
- Voltage across C1 (V1) = 200 V
- Capacitor 2 (C2) = 2 mF = 2 x 10^-3 F
- Voltage across C2 (V2) = 100 V
U1=12C1V12
U1=12×2×10−3×(200)2
U1=12×2×10−3×40000
U1=40 joules
U2=12C2V22
U2=12×2×10−3×(100)2
U2=12×2×10−3×10000
U2=10 joules
U=U1+U2=40+10=50 joules
- Charge on C1 (Q1):
Q1=C1×V1=2×10−3×200=0.4 coulombs
- Charge on C2 (Q2):
Q2=C2×V2=2×10−3×100=0.2 coulombs
- Total charge (Q):
Q=Q1+Q2=0.4+0.2=0.6 coulombs
Ceq=C1+C2=2×10−3+2×10−3=4×10−3 F
U′=12Q2Ceq
U′=12(0.6)24×10−3
U′=120.364×10−3=0.368×10−3=45 joules
Loss of energy=U−U′=50−45=5 joules
Percentage loss=(Loss of energyU)×100
Percentage loss=(550)×100=10%
The percentage loss of energy of the system is 10%.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (CUTTENT ELECTRICITY )108videos
APPENDICES ( REVISION EXERCISE )
- BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MOVING CHANGES & MEGNETISM)95videos
APPENDICES ( REVISION EXERCISE )
- BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )52videos
APPENDICES ( REVISION EXERCISE )
- BOOK - AAKASH SERIESCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE - III24videos
ALTERNATING CURRENT
- BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION128videos
APPENDICES (REVISION EXERCISE)
Similar Questions
A condenser of capacity 16 mF charged to a potential of 20 V is connected to a condenser of capacity C charged to a potential of 10 V as shown in the figure.

If the common potential is 14 V. the capacity C is equal toView SolutionA capacitorn of 2μF charged to 50 V is connected in parallel with another capacitor of 1μF charged to 20 V. The common potential and loss of energy will be
View Solution
Knowledge Check
- Question 1 - Select One
A capacitor or capacitance C1 is charge to a potential V and then connected in parallel to an uncharged capacitor of capacitance C2. The fianl potential difference across each capacitor will be
AC1VC1+C2BC2VC1+C2C1+C2C1D1−C2C1
A capacitor of 20μF charged upto 500 V is connected in parallel with another capacitor of 10μF, which is charged upto 200 V. the common potential is
View SolutionIn the adjoining diagram, the condenser C will be fully charged to potential V if
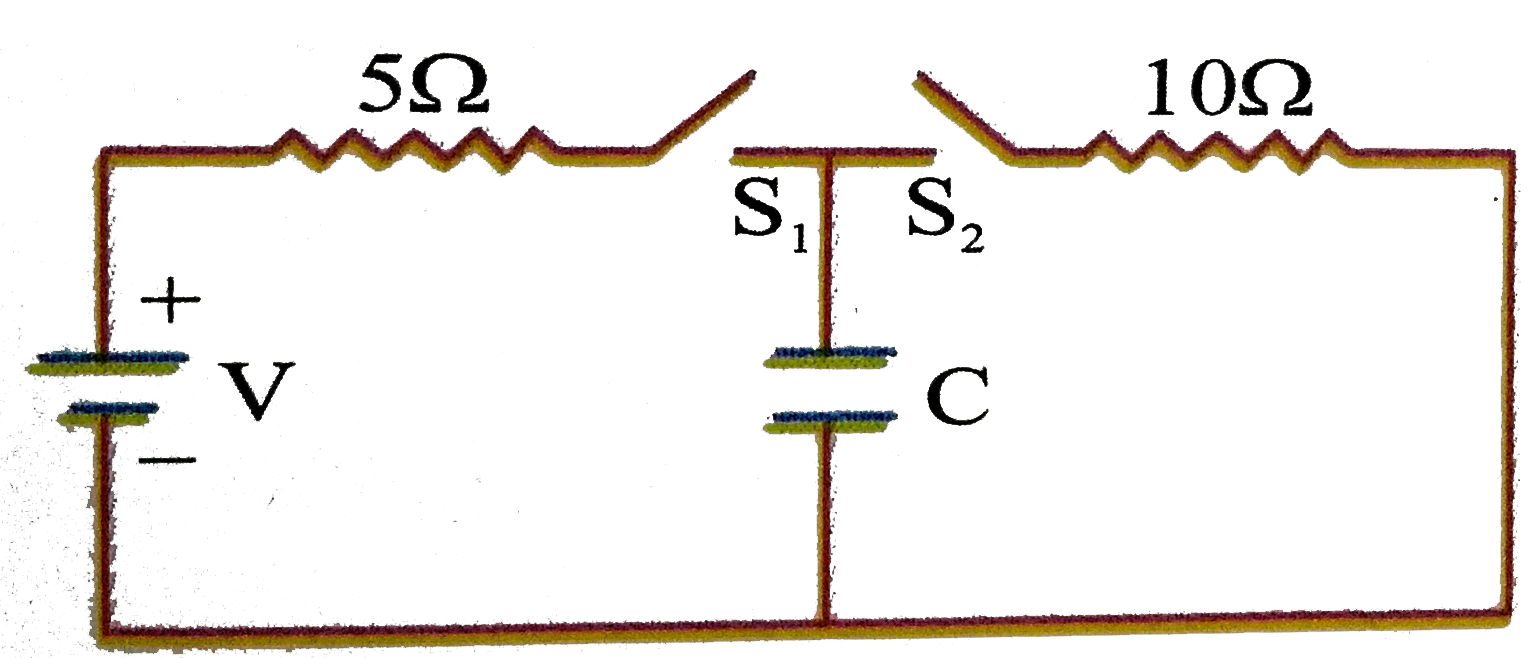 .View Solution
.View SolutionA capacitor of capacity C is charged to a potential difference V and another capacitor of capacity 2C is charged to a potential difference 4V. The charged batteries are disconnected and the two capacitors are connected with reverse polarity (i.e. positive plate of first capacitor is connected to negative plate of second capacitor). The heat produced during the redistribution of charge between the capacitors will be
View SolutionAn air capacitor is charged upto a potential V1. It is connected in parallel to an identical uncharged capacitor filled with a dielectric medium. After redistribution of charge if the potential difference of this combination is V, then the dielectric constant of the substance will be
View SolutionA charged sphere is connected to a similar uncharged sphere. Then the percentage loss of energy is
View SolutionA condenser of capacitance 10μF has been charged to 100V. It is now connected to another uncharged condenser in parallel. The common potential becomes 40V. The capacitance of another condenser is
View Solution0.2F capacitor is charged to 600V by a battery. On removing the battery it is connected with another parallel plate condenser of 1F. The potential decreases to
View Solution
