Find intensity of magnetic induction of B due to a a long current carrying conductor.
To find the intensity of magnetic induction (B) due to a long current-carrying conductor, we can follow these steps:
1. Understand the Setup:
- We have a long straight conductor carrying a current I.
- We want to find the magnetic field (B) at a distance r from the conductor.
2. Use Ampere's Circuital Law:
- According to Ampere's Circuital Law, the line integral of the magnetic field around a closed loop is proportional to the current enclosed by that loop. Mathematically, it is expressed as:
∮B⋅dl=μ0Ienc
- Here, μ0 is the permeability of free space, and Ienc is the current enclosed by the loop.
3. Consider an Amperian Loop:
- We will consider a circular Amperian loop of radius r centered around the conductor. The magnetic field B is uniform along this loop and is tangent to the loop at every point.
4. Evaluate the Line Integral:
- The left side of Ampere's law becomes:
∮B⋅dl=B∮dl=B(2πr)
- Here, 2πr is the circumference of the circular loop.
5. Set Up the Equation:
- The right side of Ampere's law is simply the current I flowing through the conductor:
μ0I
- Thus, we can set the two sides equal:
B(2πr)=μ0I
6. Solve for B:
- Rearranging the equation gives us:
B=μ0I2πr
Final Result:
The intensity of magnetic induction B due to a long current-carrying conductor at a distance r from it is given by:
B=μ0I2πr
- We have a long straight conductor carrying a current I.
- We want to find the magnetic field (B) at a distance r from the conductor.
- According to Ampere's Circuital Law, the line integral of the magnetic field around a closed loop is proportional to the current enclosed by that loop. Mathematically, it is expressed as:
∮B⋅dl=μ0Ienc
- Here, μ0 is the permeability of free space, and Ienc is the current enclosed by the loop.
- We will consider a circular Amperian loop of radius r centered around the conductor. The magnetic field B is uniform along this loop and is tangent to the loop at every point.
- The left side of Ampere's law becomes:
∮B⋅dl=B∮dl=B(2πr)
- Here, 2πr is the circumference of the circular loop.
- The right side of Ampere's law is simply the current I flowing through the conductor:
μ0I
- Thus, we can set the two sides equal:
B(2πr)=μ0I
- Rearranging the equation gives us:
B=μ0I2πr
The intensity of magnetic induction B due to a long current-carrying conductor at a distance r from it is given by:
B=μ0I2πr
Topper's Solved these Questions
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - EXERCISE (VERY SHORT ANSWER QUESTIONS )
19 Videos
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - PROBLEMS (LEVEL -I)
40 Videos
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - EXERCISE (LONG ANSWER QUESTIONS)
5 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -II
22 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
5 Videos
Similar Questions
A current of 1/(4π) ampere is flowing in a long straight conductor. The line integral of magnetic induction around a closed path enclosing the current carrying conductor is
View SolutionMagnetic induction at a point due to a small element of current carrying conductor is
View SolutionFind the magnetic induction due to a straight conductor of length 16cm carrying current of 5A at a distance of 6cm from the midpoint of conductor
View SolutionThe strength of magnetic field around an infinitely long current carrying conductor is
View SolutionThe magnetic field in a straight current carrying conductor wire is:
View SolutionThe resultant force on a square current loop PQRS due to a long current carrying conductor will be (if the current flow in the loop is clockwise)
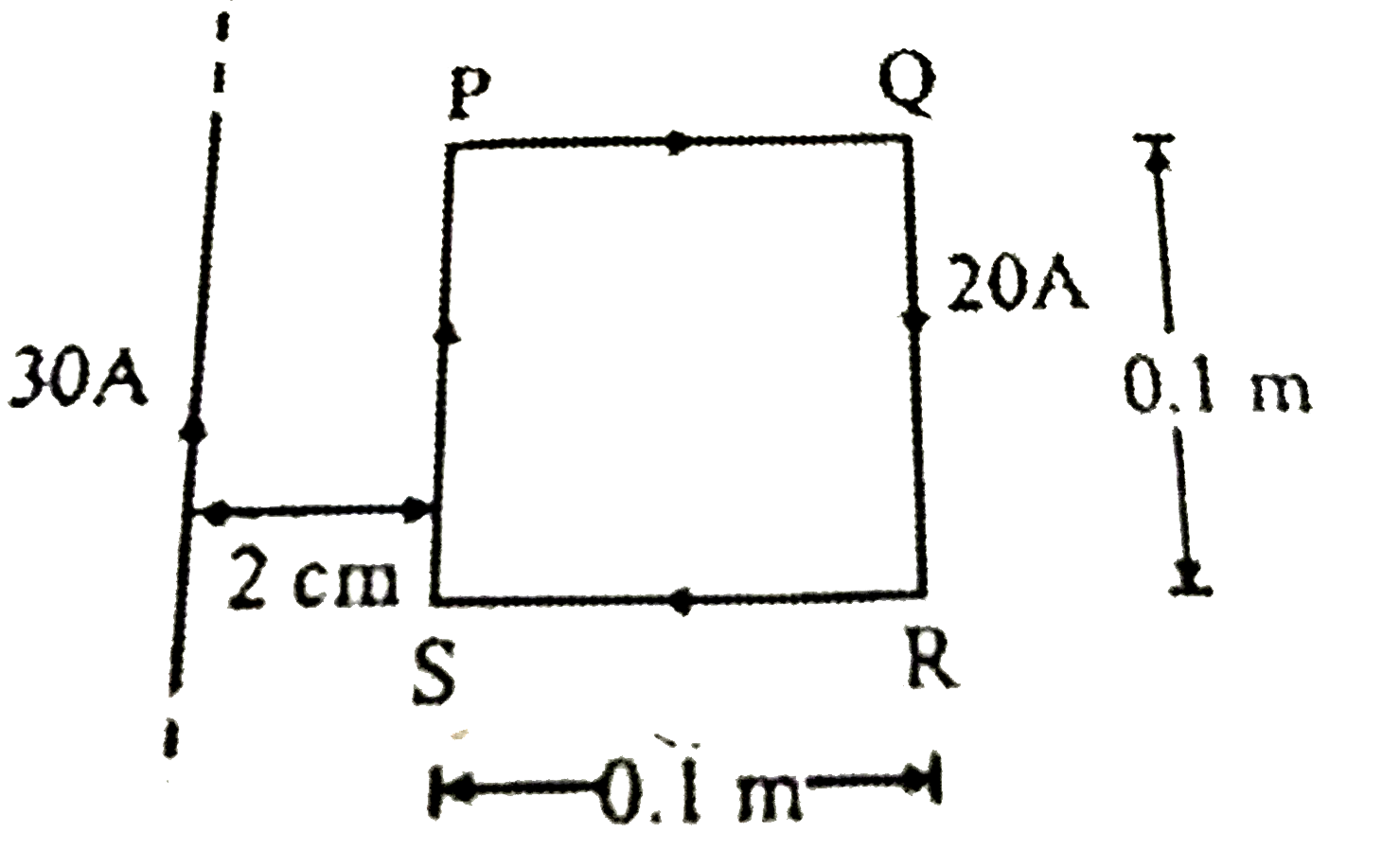
View SolutionWhich one of the following graphs shows the variation of magnetic induction B which distance r from a long wire carrying a current ?
View SolutionThe magnetic flux density at a point distant d from a long straight current carrying conductor is B, then its value at distance d2 will be-
View SolutionWith the help of a labelled circuit diagram, illustrate the pattern of field lines of the magnetic field around a current-carrying straight long conducting wire. How is the right hand thumb rule useful to find direction of magnetic field associated with a current-carrying conductor?
View SolutionMagnetic lines of force due to a straight conductor carrying current are
View Solution
