A long horizontal rigidly supported wire carriers a current ia=96A. Directly above it and parallel to it at a distance, another wire of 0.144 N weight per metre carries a current ib=24 A, in a direction opposite to that of ia If the upper wire is to float in air due to magnetic repulsion, what is its distance (in mm) from the lower wire ?
To solve the problem, we need to find the distance D between the two wires such that the magnetic repulsion force equals the weight of the upper wire. Let's break this down step by step.
Step 1: Understand the Forces Acting on the Upper Wire
The upper wire experiences two forces:
1. The downward gravitational force (weight) due to its mass.
2. The upward magnetic force due to the current in the lower wire.
Step 2: Calculate the Weight of the Upper Wire
The weight per unit length of the upper wire is given as 0.144N/m. Therefore, the total weight W acting downward on the upper wire can be expressed as:
W=0.144N/m
Step 3: Write the Expression for Magnetic Force
The magnetic force per unit length F/L between two parallel current-carrying wires is given by:
F/L=μ0IaIb2πD
where:
- μ0=4π×10−7T m/A (the permeability of free space),
- Ia=96A (current in the lower wire),
- Ib=24A (current in the upper wire),
- D is the distance between the wires.
Step 4: Set the Forces Equal for Equilibrium
For the upper wire to float, the magnetic force must equal the weight:
μ0IaIb2πD=W
Step 5: Substitute Known Values
Substituting the known values into the equation:
4π×10−7×96×242πD=0.144
Step 6: Simplify the Equation
Cancel π from both sides:
4×10−7×96×242D=0.144
This simplifies to:
2×10−7×96×24D=0.144
Step 7: Solve for Distance D
Rearranging gives:
D=2×10−7×96×240.144
Step 8: Calculate the Value
Now, calculate the numerator:
2×10−7×96×24=4.608×10−5
Now divide by 0.144:
D=4.608×10−50.144≈3.2×10−4m
Step 9: Convert to Millimeters
To convert meters to millimeters:
D=3.2×10−4m=3.2mm
Final Answer
The distance D between the two wires for the upper wire to float is:
3.2mm
The upper wire experiences two forces:
1. The downward gravitational force (weight) due to its mass.
2. The upward magnetic force due to the current in the lower wire.
The weight per unit length of the upper wire is given as 0.144N/m. Therefore, the total weight W acting downward on the upper wire can be expressed as:
W=0.144N/m
The magnetic force per unit length F/L between two parallel current-carrying wires is given by:
F/L=μ0IaIb2πD
where:
- μ0=4π×10−7T m/A (the permeability of free space),
- Ia=96A (current in the lower wire),
- Ib=24A (current in the upper wire),
- D is the distance between the wires.
For the upper wire to float, the magnetic force must equal the weight:
μ0IaIb2πD=W
Substituting the known values into the equation:
4π×10−7×96×242πD=0.144
Cancel π from both sides:
4×10−7×96×242D=0.144
This simplifies to:
2×10−7×96×24D=0.144
Rearranging gives:
D=2×10−7×96×240.144
Now, calculate the numerator:
2×10−7×96×24=4.608×10−5
Now divide by 0.144:
D=4.608×10−50.144≈3.2×10−4m
To convert meters to millimeters:
D=3.2×10−4m=3.2mm
The distance D between the two wires for the upper wire to float is:
3.2mm
Topper's Solved these Questions
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - PROBLEMS (LEVEL -II)
40 Videos
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - ADDITIONAL EXERCISE
13 Videos
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - EXERCISE (VERY SHORT ANSWER QUESTIONS )
19 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -II
22 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
5 Videos
Similar Questions
An element has a face-centred cubic (fcc) structure with a cell edge of a. The distance between the centres of two nearest tetrahedral voids in the lattice is:
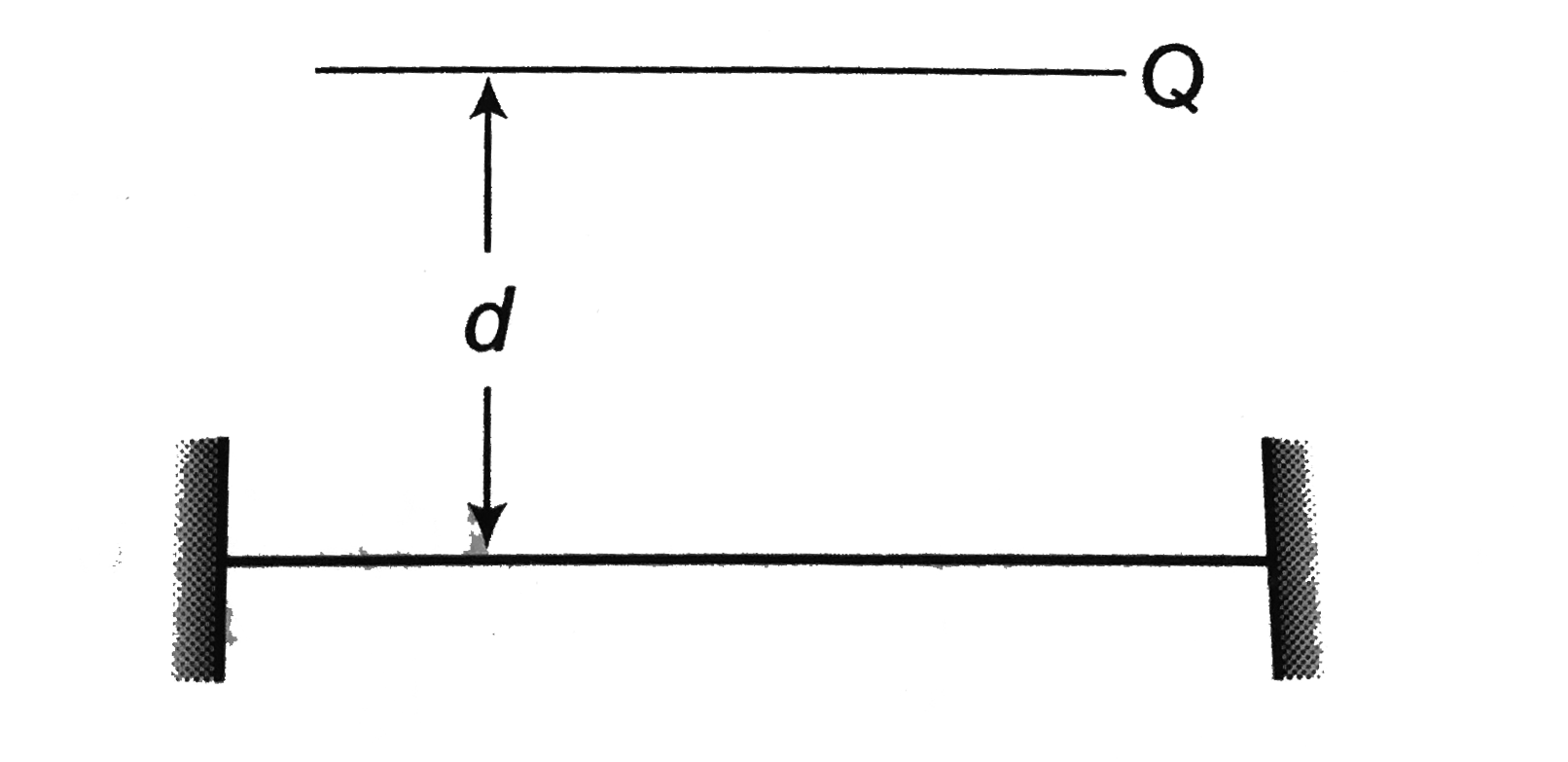
View SolutionA long horizontal wire P carries of 50A. It is rigidly fixed. Another fine wire Q is placed directly above and parallel to P. The wieght of wire Q is 0.075N/m and carries a current of 25A. Find the position of wire Q from P so that the wire Q remains suspended due to magnetic repulsion.
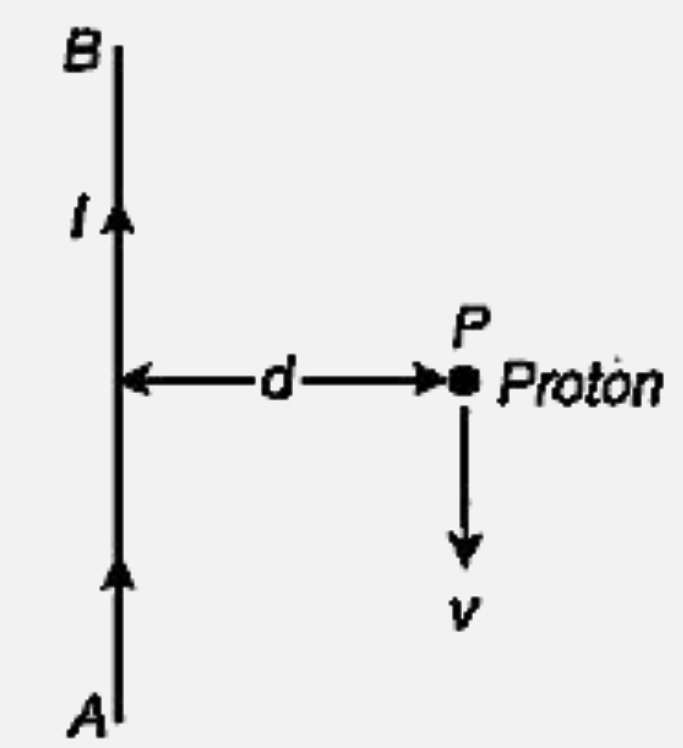
View SolutionA long straight wire AB carries a current I. A proton P travels with a speed v, parallel to the wire at a distance d from it in a direction opposite to the current as shown in the figure. What is the force experienced by the proton and what is its direction?
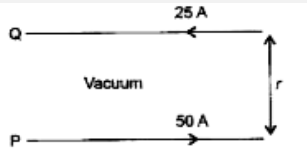
View SolutionA long horizontal wire P carries a current of 50A. It is rigidly fixed. Another wire Q is placed directly above and parallel to P, as shown in figure below. The weight per unit length of the wire Q is 0.025 Nm−1 and it carries a current of 25A. Find the distance .r. of the wire Q from the wire P so that the wire Q remains at rest.
View SolutionFind →B at the origin due to the long wire carrying a current I

View SolutionAn electric current passes through a long straight copper wire. At a distance of 5 cm from the straight wire, the magnetic field is B. What is the magnetic field at a distance of 20 cm from the wire ?
View SolutionA long copper wire carries a current of I ampere. Calculate the magnetic flux per meter of the wire for a plane surface S inside the wire as shown in Fig.

View SolutionFind →B at the origin due to the long wire carrying current I.

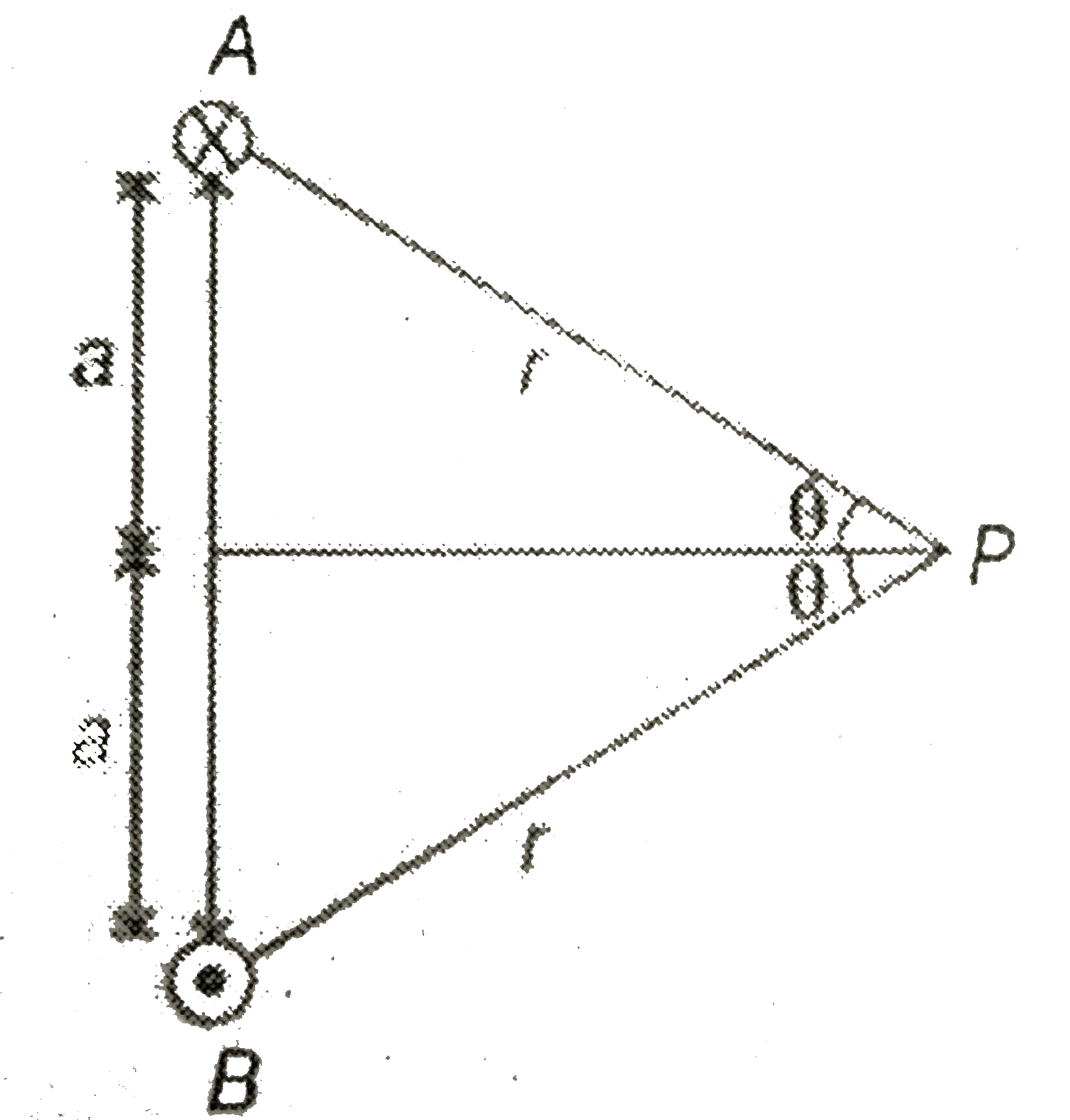
View SolutionTwo long parallel wire A and B situated perpendicuilar to the plane of the paper at a distance 2a are carrying equal currents I in opposite direction as show in the figure . The value of magnetic induction at point P situated at equal distance r from both the wires will be
View SolutionA rod of length l is kept parallel to a long wire carrying constant current i . It is moving away from the wire with a velocity v. Find the emf induced in the wire when its distance from the long wire is x.
View Solution
