The harmonic wave yi=(2.0×10−3)cosπ(2.0x−50t) travels along a string towards a boundary at x=0 with a second string. The wave speed on the second string is 50m/s. Write expressions for reflected and transmitted waves. Assume SI units.
(a) (6.67×10−4)cosπ(2.0x+50t)
(b) (2.67×10−3)cosπ(1.0x−50t) SI units
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - PROBLEMS (LEVEL - I)59videos
WAVE MOTION AND SOUND
- BOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - PRACTICE SHEET ADVANCED (INTEGER TYPE QUESTIONS)10videos
WAVE MOTION
- BOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - PROBLEMS (LEVEL - II)33videos
WAVE OPTICS
Similar Questions
A wave yi=0.3cos(2.0x−40t) is travelling along a string toward a boundary at x=0. Write expressions for the reflected waves if .
(a) the string has a fixed end at x=0 and
(b) The string has a free end at x=0.
Assume SI units.View SolutionA travelling wave y=Asin(kx−ωt+θ) passes from a heavier string to a lighter string . The juction of the strings is at x=0. The equation of the reflected wave is
View SolutionA harmonic wave is travelling on string 1. At a junction with string 2 it is partly reflected and partly transmitted. The linear mass density of the second string is four times that of the first string, and that the boundary between the two strings is at x=0. If the expression for the incident wave is
yi=Aicos(k1x−ω1t)
(a) What are the expressions for the transmitted and the reflected waves in terms of Ai,k1 and ω1?
(b) Show that the average power carried by the incident wave is equal to the sum of the average power carried by the transmitted and reflected waves.View SolutionA travelling wave y=Asin(kx−ωt+θ) passes from a heavier string to a lighter string. The reflected wave has amplitude 0.5A . The junction of the strings is at x=0. The equation fo the refelcted wave is :
View SolutionA wave pulse on a string on a string has the dimension shown in figure. The wave speed is v=1 cm /s . If point O is a free end. The shape of wave at time t = 3s si
 View Solution
View SolutionThe displacement wave in a string is y=(3cm)sin6.28(0.5x−50t) where x is in centimetres and t in seconds. The velocity and wavelength of the wave is :-
View SolutionA travelling wave y=Asin(kx−ωt+θ) passes from a heavier string to a lighter string. The reflected wave has amplitude 0.5A. The junction of the string is at x=0 The equation of the reflected is :
View SolutionThe wave described by y =0.25sin(10πx−2πt) where x and y are in meters and t in seconds , is a wave travelling along the
View SolutionTransverse waves travel with a speed of 20.0m/sin a string under a tension of 6.00 N. what tension is requared for a wave speed of 30.0m/s in the same string?
View SolutionA standing wave pattern of maximum amplitude 2 mm is obtained in a string whose shape at t = 0 is represented in the graph.
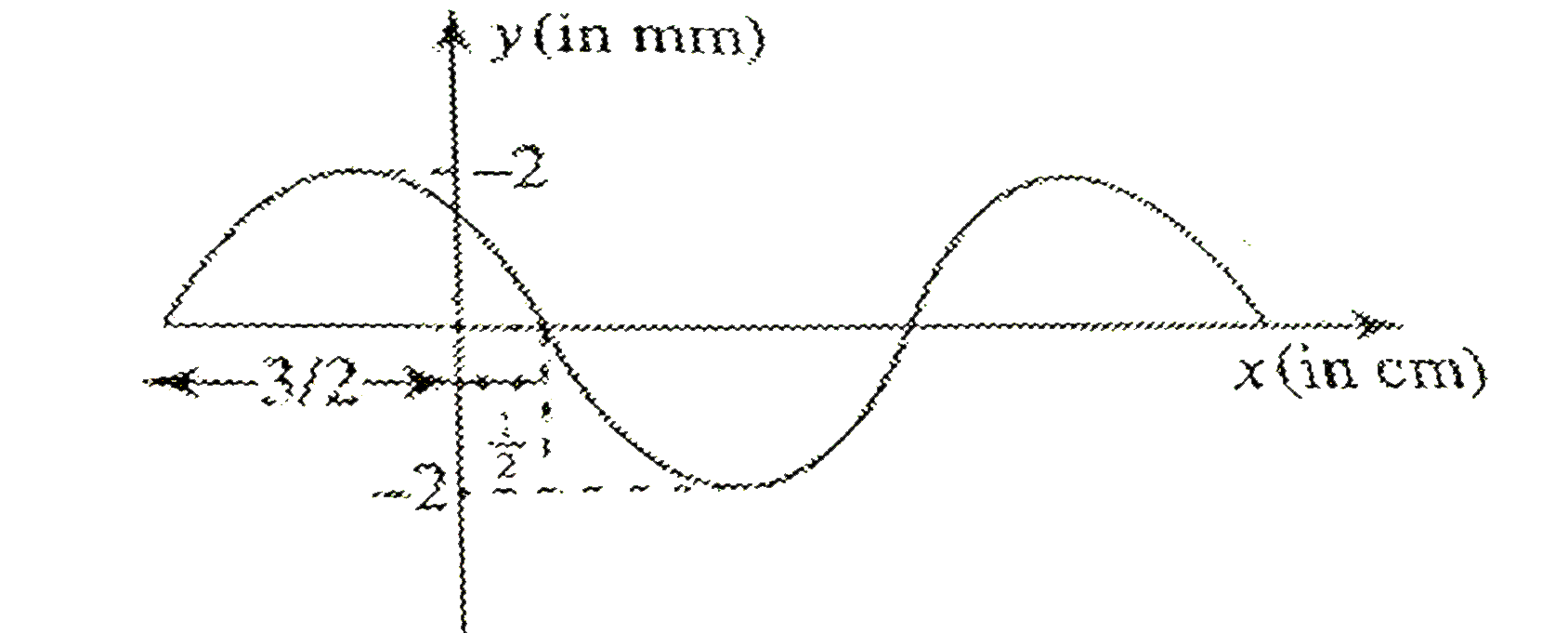
If the speed of the travelling wave in the string is 5 cm/s, then find the component waves.View Solution

