A source of sound emitting a 1200 Hz note travels along a straight line at a speed of 170 m/s. A detector is placed at a distance of 200 m from the line of motion of the source.
Find the distance between the source and the detector at the instant it detects the frequency 1200 Hz. Velocity of sound in air = 340 m/s.
To solve the problem, we need to find the distance between the source of sound and the detector when the frequency detected is 1200 Hz. Here's a step-by-step solution:
Step 1: Understand the problem
We have a sound source emitting a frequency of 1200 Hz and moving at a speed of 170 m/s. The detector is positioned 200 m away from the line of motion of the source. We need to find the distance between the source and the detector when the frequency detected is still 1200 Hz.
Step 2: Set up the scenario
Let:
- Vs=170m/s (speed of the source)
- V=340m/s (speed of sound in air)
- L=200m (perpendicular distance from the line of motion to the detector)
Step 3: Use the relationship between distances and time
The distance SD between the source and the detector can be expressed using the Pythagorean theorem. The distance SD can be calculated as:
SD=√(V⋅T)2+(Vs⋅T)2
Where T is the time taken for the sound to reach the detector.
Step 4: Express time in terms of distance
The time T can be expressed as:
T=LV
Substituting this into the equation for SD:
SD=√(V⋅LV)2+(Vs⋅LV)2
This simplifies to:
SD=√L2+(Vs⋅LV)2
Step 5: Substitute the known values
Now, substituting the known values:
SD=√2002+(170⋅200340)2
Calculating 170⋅200340:
170⋅200340=100
Now, substituting this back into the equation:
SD=√2002+1002
Calculating:
SD=√40000+10000=√50000=223.6m
Step 6: Round the answer
Rounding to the nearest meter, we find:
SD≈224m
Final Answer
The distance between the source and the detector at the instant it detects the frequency of 1200 Hz is approximately 224 meters.
---
We have a sound source emitting a frequency of 1200 Hz and moving at a speed of 170 m/s. The detector is positioned 200 m away from the line of motion of the source. We need to find the distance between the source and the detector when the frequency detected is still 1200 Hz.
Let:
- Vs=170m/s (speed of the source)
- V=340m/s (speed of sound in air)
- L=200m (perpendicular distance from the line of motion to the detector)
The distance SD between the source and the detector can be expressed using the Pythagorean theorem. The distance SD can be calculated as:
SD=√(V⋅T)2+(Vs⋅T)2
Where T is the time taken for the sound to reach the detector.
The time T can be expressed as:
T=LV
Substituting this into the equation for SD:
SD=√(V⋅LV)2+(Vs⋅LV)2
This simplifies to:
SD=√L2+(Vs⋅LV)2
Now, substituting the known values:
SD=√2002+(170⋅200340)2
Calculating 170⋅200340:
170⋅200340=100
Now, substituting this back into the equation:
SD=√2002+1002
Calculating:
SD=√40000+10000=√50000=223.6m
Rounding to the nearest meter, we find:
SD≈224m
The distance between the source and the detector at the instant it detects the frequency of 1200 Hz is approximately 224 meters.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - PROBLEMS (LEVEL - I)59videos
WAVE MOTION AND SOUND
- BOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - PRACTICE SHEET ADVANCED (INTEGER TYPE QUESTIONS)10videos
WAVE MOTION
- BOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - PROBLEMS (LEVEL - II)33videos
WAVE OPTICS
Similar Questions
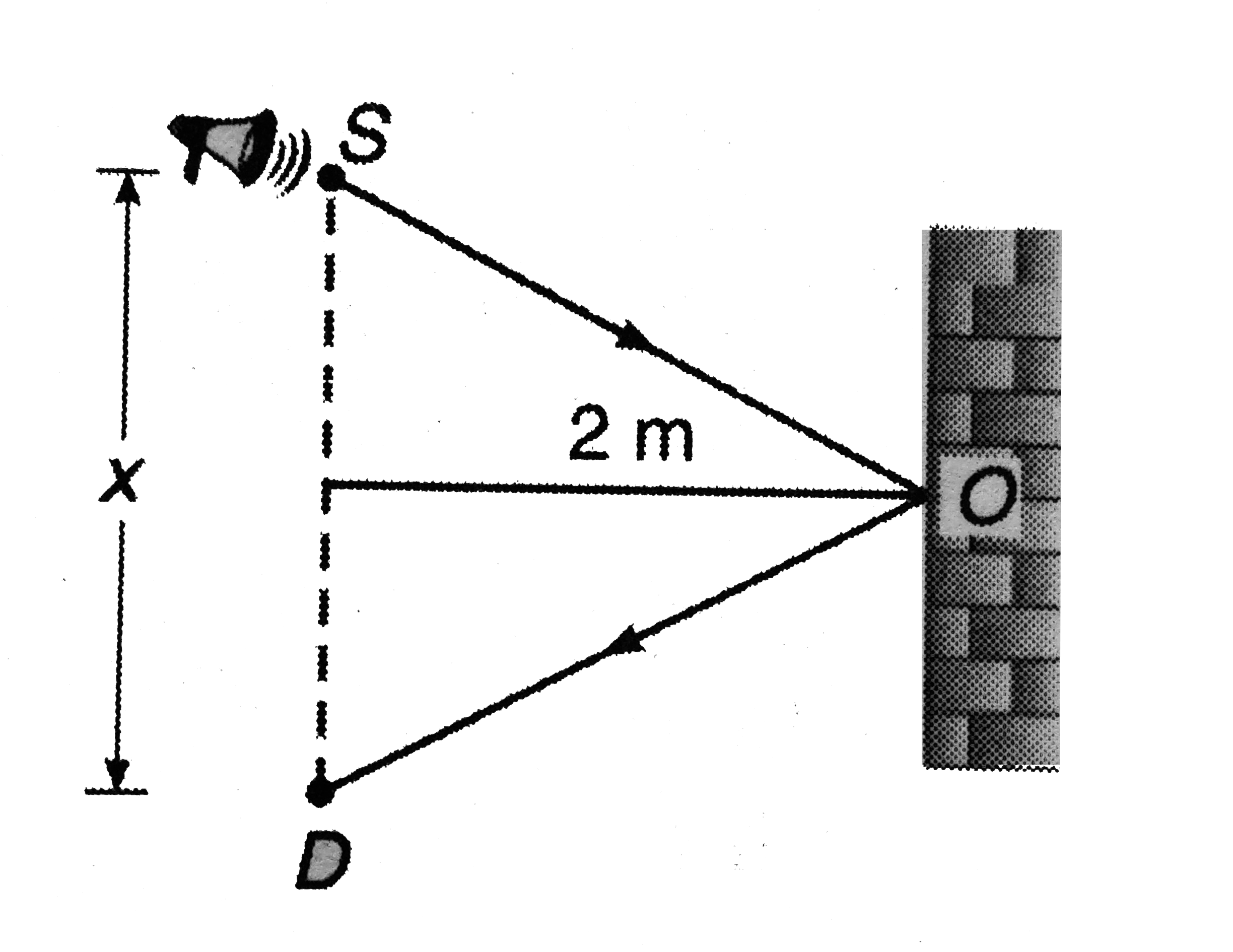
A soure of sound of frequency 165 hz is placed in front of a wall at a distance 2 m from it. A dtector is also placed in front of the wall at the same distance from it. Find the minimum distance between the source and detector for which maximum sound is recorded int he detector . the speed of sound is 330 m/s
View SolutionA source of sound emitting waves at 360HZ is placed in front of a vertical wall, at a distance 2m from it. A detector is also placed in front of the wall at the same distance from it. Find the minimum distance between the source and the detestor for which the detector detects a maximum of sound. Take speed of sound in air=360m/s. Assume that there is not phase change in reflected wave.
 View Solution
View SolutionIn an organ pipe the distance between the adjacent node is 4cm. Find the frequency of source if speed of sound in air is 336m/s.
View SolutionA source of sound of frequency 1000HZ moves unifornly along a straight line with velocity 0.8 times velocity of sound . An observer is located at a distance l=250m from this line. Find
(a) the frequency of the sound at instant when the source is closest to the observer.
(b) the distance of the source when he observer no change in the frequency.View SolutionA soure of sound of frequency 165 hz is placed in front of a wall at a distance 2 m from it. A dtector is also placed in front of the wall at the same distance from it. Find the minimum distance between the source and detector for which maximum sound is recorded int he detector . the speed of sound is 330 m/s
View SolutionA person is listening to a tone of 500Hz sitting at a distance of 450m from the source of the sound. What is the time interval between successive compressions from the source ?
View SolutionCalculate the minimum distance in air required between the source of sound and the obstacle to hear an echo. Take speed of sound in air = 350 ms−1
View SolutionA man is travelling in a train towards the station with a speed of 50 m/s. calculate the apparent frequency heard by him of whistle which is blown at the station with a frequency 200 Hz. Velocity of sound in air is 350 m/s.
View Solutionthe minimum distance between the reflecting surface and source for listening the eco of sound is ( take speed of sound 340ms)
View SolutionA source of sound emitting a frequency 660 Hz is moving counter-clockwise in a circular path of radius 2 metres with an angular velocity 15 rad/s. A recorder at a distance from the source is moving simple harmonically along a straight line with an amplitude 2 metres. The frequency of SHM is 152π per second. The arrangement is shown in figure. When the source is at point A the detector is at D. Find the maximum and minimum frequencies recorded. Velocity of sound in air at this temperature can be taken as 300 m/s
 View Solution
View Solution

