A source of sound emitting a 1200 Hz note travels along a straight line at a speed of 170 m/s. A detector is placed at a distance of 200 m from the line of motion of the source.
Find the frequency of sound received by the detector at the instant when the source gets closest to it.
To solve the problem of finding the frequency of sound received by the detector when the source is closest to it, we can use the Doppler effect formula. Here are the steps to arrive at the solution:
Step 1: Understand the Doppler Effect
The Doppler effect describes the change in frequency (or wavelength) of a wave in relation to an observer who is moving relative to the wave source. When the source of sound is moving towards a stationary observer, the frequency observed increases.
Step 2: Identify Given Values
- Frequency of the source, fs=1200Hz
- Speed of the source, vs=170m/s
- Speed of sound in air, v=343m/s (assuming standard conditions)
- Distance from the line of motion to the detector, d=200m
Step 3: Determine the Closest Approach
At the instant when the source is closest to the detector, it is directly perpendicular to the line connecting the source and the detector. The distance from the source to the detector can be calculated using the Pythagorean theorem:
r=√d2+(vst)2
However, at the closest point, we can simplify our calculation by focusing on the frequency change.
Step 4: Apply the Doppler Effect Formula
The formula for the observed frequency f′ when the source is moving towards a stationary observer is given by:
f′=fs(v+vsv)
Where:
- f′ = observed frequency
- fs = source frequency
- v = speed of sound
- vs = speed of the source
Step 5: Substitute the Values
Now we can substitute the values into the Doppler effect formula:
f′=1200(343+170343)
f′=1200(513343)
Step 6: Calculate the Observed Frequency
Calculating the fraction:
f′=1200×1.495≈1794Hz
Final Answer
The frequency of sound received by the detector at the instant when the source gets closest to it is approximately 1794 Hz.
---
The Doppler effect describes the change in frequency (or wavelength) of a wave in relation to an observer who is moving relative to the wave source. When the source of sound is moving towards a stationary observer, the frequency observed increases.
- Frequency of the source, fs=1200Hz
- Speed of the source, vs=170m/s
- Speed of sound in air, v=343m/s (assuming standard conditions)
- Distance from the line of motion to the detector, d=200m
At the instant when the source is closest to the detector, it is directly perpendicular to the line connecting the source and the detector. The distance from the source to the detector can be calculated using the Pythagorean theorem:
r=√d2+(vst)2
However, at the closest point, we can simplify our calculation by focusing on the frequency change.
The formula for the observed frequency f′ when the source is moving towards a stationary observer is given by:
f′=fs(v+vsv)
Where:
- f′ = observed frequency
- fs = source frequency
- v = speed of sound
- vs = speed of the source
Now we can substitute the values into the Doppler effect formula:
f′=1200(343+170343)
f′=1200(513343)
Calculating the fraction:
f′=1200×1.495≈1794Hz
The frequency of sound received by the detector at the instant when the source gets closest to it is approximately 1794 Hz.
Topper's Solved these Questions
- WAVE MOTION AND SOUNDBOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - PROBLEMS (LEVEL - I)
59 Videos
- WAVE MOTIONBOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - PRACTICE SHEET ADVANCED (INTEGER TYPE QUESTIONS)
10 Videos
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - PROBLEMS (LEVEL - II)
33 Videos
Similar Questions
A source of sound of frequency 1.8kHz moves uniformly along a straight line at a distance 250m from observer. The velocity of source is 0.8C where C is the velocity of sound. Find out the frequency of sound received by observer (in kHz) at the moment when the source gets closest to him.
View SolutionA source of sound of frequency 1000HZ moves unifornly along a straight line with velocity 0.8 times velocity of sound . An observer is located at a distance l=250m from this line. Find
(a) the frequency of the sound at instant when the source is closest to the observer.
(b) the distance of the source when he observer no change in the frequency.
View SolutionA source of sound with natural frequency f0=1800Hz moves uniformly along a straight line separated from a stationary observer by a distance l=250m. The velocity of the source is equal to η=0.80 fraction of the velocity of the sound.
Q. Find the frequency of osund received by the observer at the moment when the source gets closest to him.

View SolutionA source of sound with natural frequency f0=1800Hz moves uniformly along a straight line separated from a stationary observer by a distance l=250m. The velocity of the source is equal to η=0.80 fraction of the velocity of the sound.
Q. Find the frequency of osund received by the observer at the moment when the source gets closest to him.

View SolutionA source of sound with natural frequency f0=1800Hz moves uniformly along a straight line separated from a stationary observer by a distance l=250m. The velocity of the source is equal to η=0.80 fraction of the velocity of the sound.
Q. The distance between the source and the observer at the moment when the observer receives a frequency f=f0 is

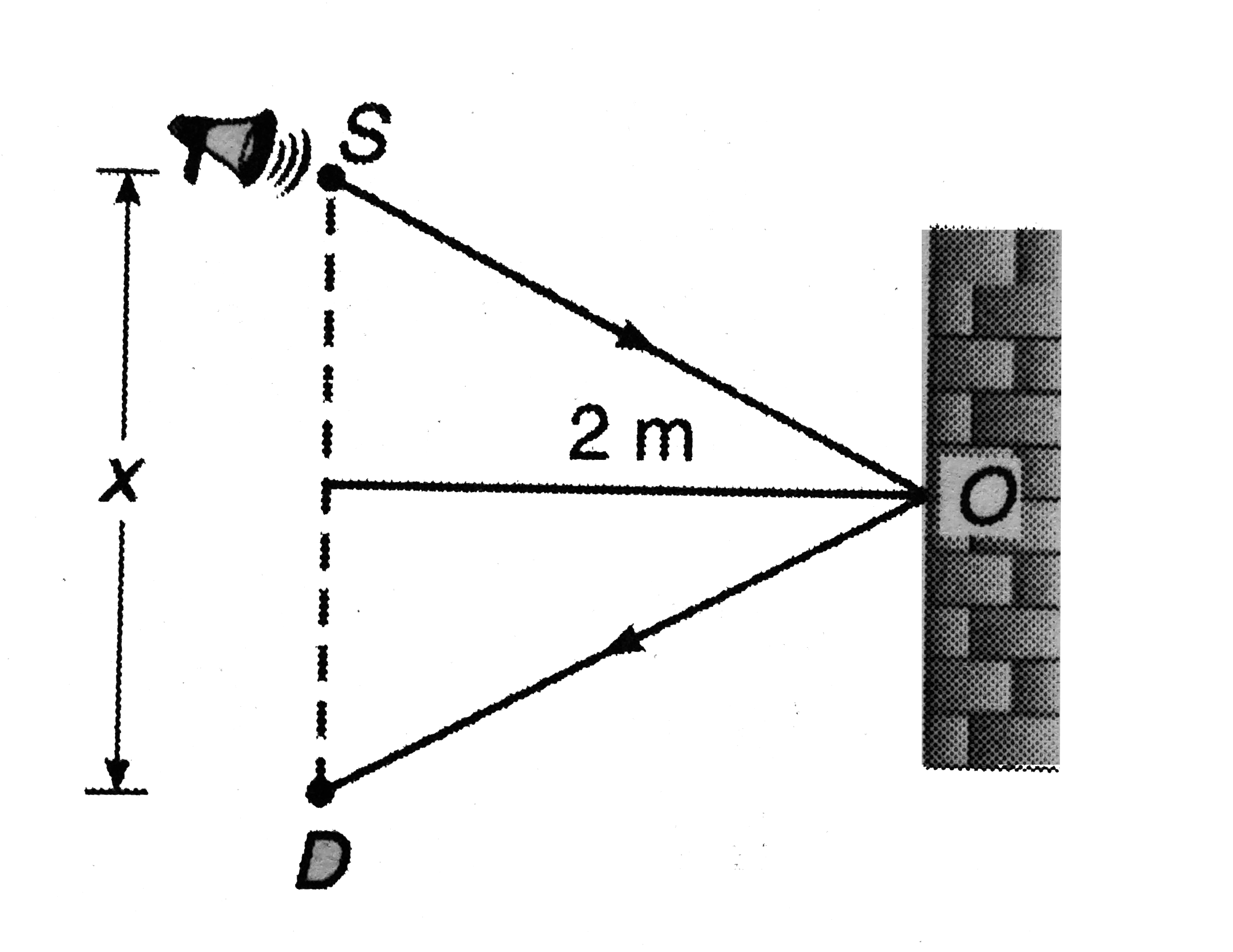
View SolutionA source of sound emitting waves at 360HZ is placed in front of a vertical wall, at a distance 2m from it. A detector is also placed in front of the wall at the same distance from it. Find the minimum distance between the source and the detestor for which the detector detects a maximum of sound. Take speed of sound in air=360m/s. Assume that there is not phase change in reflected wave.
View SolutionThe figure shows the location of a source and detector at time t = 0. The source and detector are moving with velocities vs=5ˆims−1andvD=10ˆjms−1 respectively . The frequency of signals received by the detector at the moment when the source cros the origin is (the frequency of the source is 100 Hz . Velocity bof sound 330ms−1 .)

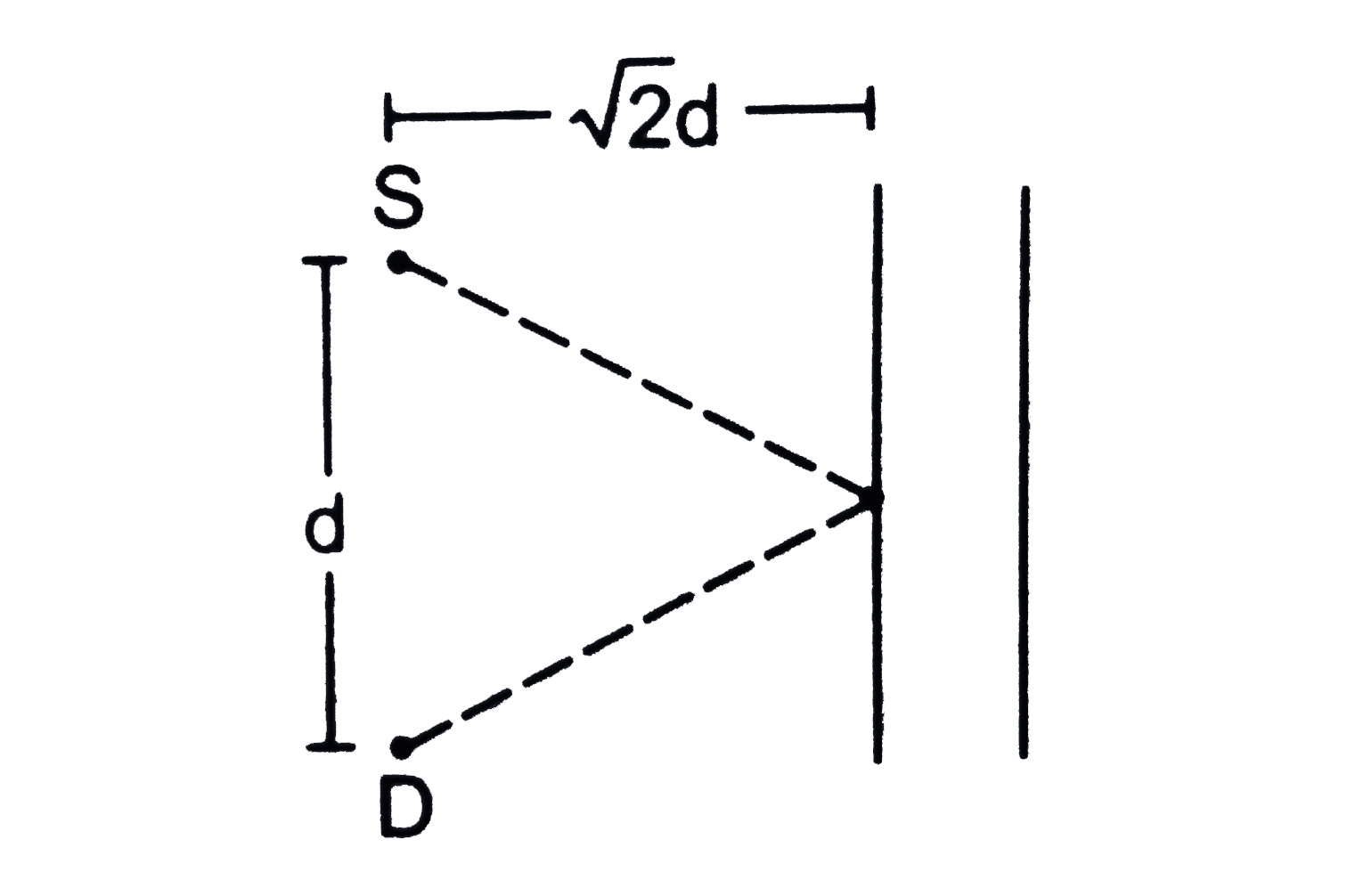
View SolutionA source S and a detector D are placed at a distance d apart. A big cardboard is placed at a distance √2d from the source and the detector as shown in figure. The source emits a wave of wavelength =d2 which is received by the detector after reflection from the cardboard. It is found to be in phase with the direct wave received from the source. By what minimum distance should the cardboard be shifted away so that the reflected wave becomes out of phase with the direct wave ?
View SolutionA soure of sound of frequency 165 hz is placed in front of a wall at a distance 2 m from it. A dtector is also placed in front of the wall at the same distance from it. Find the minimum distance between the source and detector for which maximum sound is recorded int he detector . the speed of sound is 330 m/s
View SolutionA source and a detector move away from each other, each with a speed of 10 m/s with respect to ground with no wind. If the detector detects a frequency 1650 Hz of the sound coming from the source, what is the original frequency of the source? (speed of sound = 340 m/s
View Solution
