Two spheres of masses 4 kg and 8 kg are moving with velocities 2ms−1and3ms−1 away from each other along the same line. The velocity of centre of mass is
83ms−1 towards second sphere
83ms−1 towards first sphere
43ms−1 towards second sphere
43ms−1 towards first sphere
The correct Answer is:A
To find the velocity of the center of mass of the two spheres, we can follow these steps:
Step 1: Identify the masses and velocities
- Mass of the first sphere, m1=4kg
- Velocity of the first sphere, v1=−2m/s (negative because it is moving in the opposite direction)
- Mass of the second sphere, m2=8kg
- Velocity of the second sphere, v2=3m/s (positive because it is moving in the positive direction)
Step 2: Write the formula for the velocity of the center of mass
The velocity of the center of mass Vcm is given by the formula:
Vcm=m1v1+m2v2m1+m2
Step 3: Substitute the values into the formula
Substituting the values we have:
Vcm=(4kg)(−2m/s)+(8kg)(3m/s)4kg+8kg
Step 4: Calculate the numerator and denominator
Calculating the numerator:
=(4×−2)+(8×3)=−8+24=16
Calculating the denominator:
=4+8=12
Step 5: Calculate the velocity of the center of mass
Now, substituting back into the equation:
Vcm=1612=43m/s
Step 6: Determine the direction of the center of mass velocity
Since the result is positive, it indicates that the center of mass is moving in the direction of the second sphere (which is the positive direction).
Final Answer:
The velocity of the center of mass is 43m/s towards the second sphere.
---
- Mass of the first sphere, m1=4kg
- Velocity of the first sphere, v1=−2m/s (negative because it is moving in the opposite direction)
- Mass of the second sphere, m2=8kg
- Velocity of the second sphere, v2=3m/s (positive because it is moving in the positive direction)
The velocity of the center of mass Vcm is given by the formula:
Vcm=m1v1+m2v2m1+m2
Substituting the values we have:
Vcm=(4kg)(−2m/s)+(8kg)(3m/s)4kg+8kg
Calculating the numerator:
=(4×−2)+(8×3)=−8+24=16
Calculating the denominator:
=4+8=12
Now, substituting back into the equation:
Vcm=1612=43m/s
Since the result is positive, it indicates that the center of mass is moving in the direction of the second sphere (which is the positive direction).
The velocity of the center of mass is 43m/s towards the second sphere.
Similar Questions
Particles of masses 1kg and 3kg are moving with the velocities (10i−7j−3k)ms−1 and (7i−9j+6k)ms−1 then the instantaneous velocity of their centre of mass is
View SolutionTwo bodies of different masses 2kg and 4kg are moving with velocities 2m/s and 10m/s towards each other due to mutual gravitational attraction. Then the velocity of the centre of mass is
View SolutionTwo bodies of masses 3 kg and 2 kg are moving towards wach other with 3ms−1 and 2ms−1 respectively. Then velocity of centre of mass is
View SolutionTwo bodies of masses 4kg and 2kg are moving towards each other with 3ms−1 and 2ms−1 respectively. Then velocity of centre of mass is
View SolutionTwo bodies of mases 5kg and 3kg are moving towards each other with 2ms−1 and 4ms−1 respectively. Then velocity of centre of mass is
View SolutionTwo particles of masses 3kg and 2kg move due north and due east respectively with the velocities2ms−1and3ms−1. The magnitude and direction of the velocity of centre of mass is
View SolutionTwo particles of masses 2 kg and 4 kg are approaching each other with acceleration 1ms−2 and 2ms−2, respectively, on a smooth horizontal surface. Find the acceleration of center of mass of the system.
View SolutionTwo bodies of masses 1 kg and 2 kg moving with same velocities are stopped by the same force. Then, the ratio of their stopping distances is
View SolutionThree small balls of masses 1kg, 2kg and 3kg are moving in a plane and their velocities are 1ms−1,2ms−2and3ms−1 respectively as shown . The total angular momentum of the system of three balls about point P at the given instant of time is
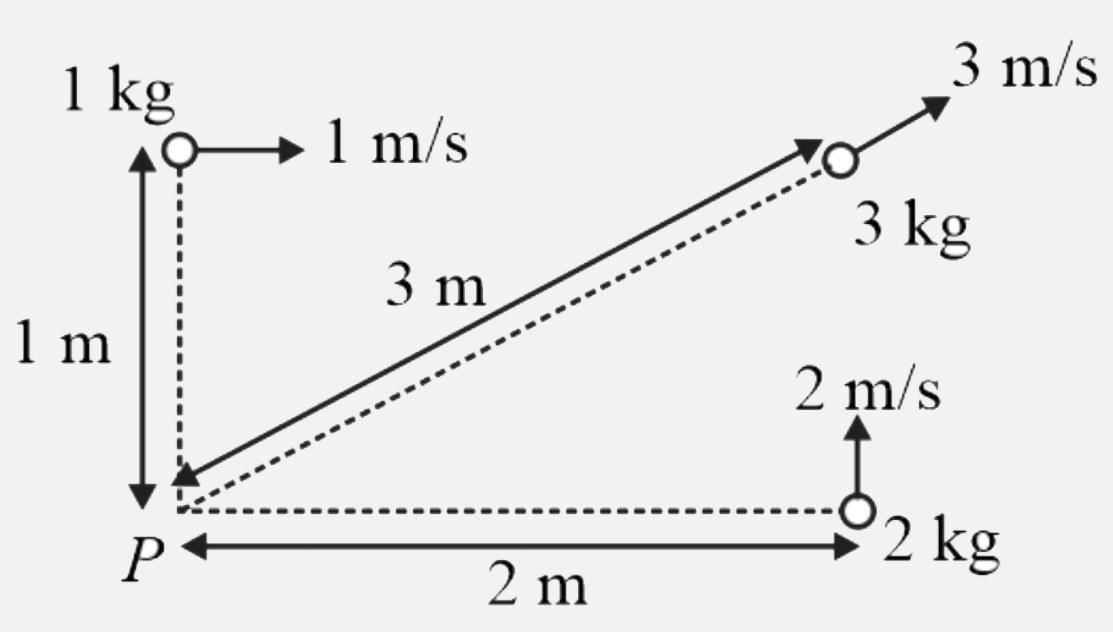 View Solution
View SolutionTwo smooth spheres A and B of masses 4kg and 8kg move with velocities 9m/s and 3m/s in opposite directions. If A rebounds on its path with velocity 1m/s, then
View Solution

