Particles of masses 1kg and 3kg are moving with the velocities (10i−7j−3k)ms−1 and (7i−9j+6k)ms−1 then the instantaneous velocity of their centre of mass is
14(31i−34j+15k)ms−1
14(30i−32j+15k)ms−1
14(25i−28j+15k)ms−1
14(31i−34j+20k)ms−1
The correct Answer is:A
To find the instantaneous velocity of the center of mass of two particles with given masses and velocities, we can follow these steps:
Step 1: Identify the masses and velocities
- Mass of particle 1, m1=1kg
- Velocity of particle 1, v1=(10i−7j−3k)m/s
- Mass of particle 2, m2=3kg
- Velocity of particle 2, v2=(7i−9j+6k)m/s
Step 2: Use the formula for the velocity of the center of mass
The formula for the velocity of the center of mass (Vcm) is given by:
Vcm=m1v1+m2v2m1+m2
Step 3: Substitute the values into the formula
Substituting the values we have:
Vcm=1⋅(10i−7j−3k)+3⋅(7i−9j+6k)1+3
Step 4: Calculate the numerator
Calculating the individual components:
1. For m1v1:
1⋅(10i−7j−3k)=10i−7j−3k
2. For m2v2:
3⋅(7i−9j+6k)=21i−27j+18k
Now, adding these two results together:
(10i−7j−3k)+(21i−27j+18k)=(10+21)i+(−7−27)j+(−3+18)k
This simplifies to:
31i−34j+15k
Step 5: Divide by the total mass
Now, divide by the total mass:
Vcm=31i−34j+15k4
Step 6: Final result
This gives us:
Vcm=314i−344j+154k
Thus, the instantaneous velocity of the center of mass is:
Vcm=7.75i−8.5j+3.75km/s
- Mass of particle 1, m1=1kg
- Velocity of particle 1, v1=(10i−7j−3k)m/s
- Mass of particle 2, m2=3kg
- Velocity of particle 2, v2=(7i−9j+6k)m/s
The formula for the velocity of the center of mass (Vcm) is given by:
Substituting the values we have:
Calculating the individual components:
1⋅(10i−7j−3k)=10i−7j−3k
3⋅(7i−9j+6k)=21i−27j+18k
Now, divide by the total mass:
This gives us:
Similar Questions
Two spheres of masses 4 kg and 8 kg are moving with velocities 2ms−1and3ms−1 away from each other along the same line. The velocity of centre of mass is
View Solution(b) Two bodies of masses 10kg and 2 kg are moving with velocities 2ˆi−7ˆj+3ˆk and −10ˆi+35ˆj−3ˆkm/s respectively. Find the velocity of the centre of mass.
View Solution
Knowledge Check
Two bodies of masses 10kgand2kg are moving with velocities (2ˆi−7ˆj+3ˆk)and(−10ˆi+35ˆj−3ˆk)m/s respectively. Calculate the velocity of their centre of mass.
A1. 2ˆims−1B2. 2ˆkms−1C3. (2ˆj+2ˆk)ms−1D4. (2ˆi+2ˆj+2ˆk)ms−1
Two particles of masses 3kg and 2kg move due north and due east respectively with the velocities2ms−1and3ms−1. The magnitude and direction of the velocity of centre of mass is
View SolutionParticles of masses 1kg and 2kg are at (i+2j+3k) m and (−2i+4j+2k)m then instantaneous position of their centre of mass is
View SolutionParticles of masses 1 kg and 3 kg at (2i+5j+13k) m and (−6i+4j−2k)m then instantaneous position of their centre of mass is
View SolutionTwo bodies of masses 3 kg and 2 kg are moving towards wach other with 3ms−1 and 2ms−1 respectively. Then velocity of centre of mass is
View SolutionTwo bodies of masses 4kg and 2kg are moving towards each other with 3ms−1 and 2ms−1 respectively. Then velocity of centre of mass is
View SolutionTwo bodies of mases 5kg and 3kg are moving towards each other with 2ms−1 and 4ms−1 respectively. Then velocity of centre of mass is
View SolutionThree small balls of masses 1kg, 2kg and 3kg are moving in a plane and their velocities are 1ms−1,2ms−2and3ms−1 respectively as shown . The total angular momentum of the system of three balls about point P at the given instant of time is
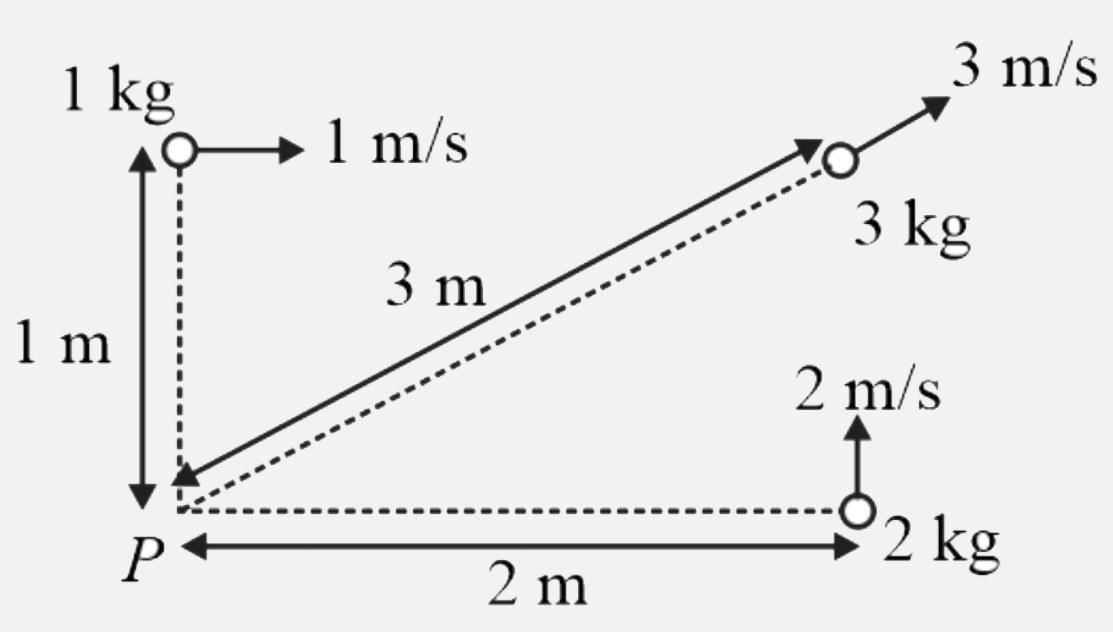
View Solution
