Particles of masses 1kg and 3kg are at 2i+5j+13k)m and (−6i+4j−2k)m then instantaneous position of their centre of mass is
14(−16i+17j+7k)m
14(−8i+17j+7k)m
14(−6i+17j+7k)m
14(−6i+17j+5k)m
The correct Answer is:A
To find the instantaneous position of the center of mass of two particles, we can use the formula for the center of mass (R_cm) given by:
Rcm=m1⋅r1+m2⋅r2m1+m2
where:
- m1 and m2 are the masses of the particles,
- r1 and r2 are their respective position vectors.
Step 1: Identify the given values
- Mass of the first particle, m1=1kg
- Position vector of the first particle, r1=2i+5j+13k
- Mass of the second particle, m2=3kg
- Position vector of the second particle, r2=−6i+4j−2k
Step 2: Substitute the values into the center of mass formula
Substituting the known values into the formula:
Rcm=1⋅(2i+5j+13k)+3⋅(−6i+4j−2k)1+3
Step 3: Calculate the numerator
Calculating each term in the numerator:
1. For the first particle:
1⋅(2i+5j+13k)=2i+5j+13k
2. For the second particle:
3⋅(−6i+4j−2k)=−18i+12j−6k
Now, combine these results:
Rcm=(2i+5j+13k)+(−18i+12j−6k)4
Step 4: Simplify the numerator
Combine the vectors:
=(2−18)i+(5+12)j+(13−6)k4
=−16i+17j+7k4
Step 5: Final expression for the center of mass
Now, divide each component by 4:
Rcm=−4i+174j+74k
Conclusion
Thus, the instantaneous position of the center of mass is:
Rcm=14(−16i+17j+7k)
Final Answer
The correct answer is option A:
14(−16i+17j+7k)
- m1 and m2 are the masses of the particles,
- r1 and r2 are their respective position vectors.
- Mass of the first particle, m1=1kg
- Position vector of the first particle, r1=2i+5j+13k
- Mass of the second particle, m2=3kg
- Position vector of the second particle, r2=−6i+4j−2k
Substituting the known values into the formula:
Calculating each term in the numerator:
1⋅(2i+5j+13k)=2i+5j+13k
3⋅(−6i+4j−2k)=−18i+12j−6k
Rcm=(2i+5j+13k)+(−18i+12j−6k)4
Combine the vectors:
=(2−18)i+(5+12)j+(13−6)k4
=−16i+17j+7k4
Now, divide each component by 4:
Rcm=−4i+174j+74k
Thus, the instantaneous position of the center of mass is:
Rcm=14(−16i+17j+7k)
The correct answer is option A:
14(−16i+17j+7k)
Topper's Solved these Questions
- SYSTEM OF PARTICLESBOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level -II(H.W)
47 Videos
- SYSTEM OF PARTICLESBOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-V
72 Videos
- SYSTEM OF PARTICLESBOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - NCERT based questions
15 Videos
- PHYSICAL WORLDBOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q
10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - IV
39 Videos
Similar Questions
Two particle of mass 1 kg and 2 kg are located at x = 0 and x = 3 m. Find the position of their centre of mass.
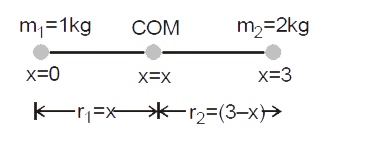
View SolutionThe coordinates of a triangle ABC are A(1,2), B(4,6) and C(−3,−2). Three particles of masses 1kg, 2kg and mkg are placed the vertices of the triangle. If the coordinate of the centre of mass are (35,2), calculate the mass m.
View Solution
Knowledge Check
Two bodies of mass 2 kg and 5 kg have position (1 m, 2 m, 1 m) and (3 m, 2 m, -1 m) respectively. The position vector of centre of mass is
A(177ˆi+2ˆj−37ˆk)mB(17ˆi+14ˆj−3ˆk)mC(2ˆi+177ˆj−37ˆk)mD(14ˆi+17ˆj−3ˆk)mTwo particles of mass 1kgand3kg have position vectors 2ˆi+3ˆj+4ˆkand−2ˆi+3ˆj−4ˆk respectively. The centre of mass has a position vector.
Aˆi+3ˆj−2ˆkB−ˆi−3ˆj−2ˆkC−ˆi+3ˆj+2ˆkD−ˆi+3ˆj−2ˆkTwo bodies of mass 1kg and 3kg have position vectors ˆi+2ˆj+ˆk and −3ˆi−2ˆj+ˆk, respectively. The centre of mass of this system has a position vector.
A−2ˆi+2ˆkB−2ˆi−ˆj+ˆkC2ˆi−ˆj−2ˆkD−1ˆi+ˆj+ˆk
The centre of mass of three particles of masses 1kg,2kgand3kg lies at the point (3m,3m,3m) where should a fourth particles of mass 4kg be positioned so that centre of mass of the four particle system at (1m,1m,1m)?
View SolutionThree particles of masses 1kg, 2kg and 3kg are placed at the corners A, B and C respectively of an equilateral triangle ABC of edge 1m. Find the distance of their centre of mass from A.
View SolutionFour particles of masses 1kg, 2kg, 3kg and 4kg are placed at the four vertices A, B, C and D of a square of side 1m. Find the position of centre of mass of the particles.
View SolutionTwo particles of masses 1kg and 2kg are located at x=0 and x=3m. Find the position of their centre of mass.
View SolutionA rigid body consists of a 3kg mass located at →r1=(2ˆi+5ˆj)m and a 2kg mass located at →r2=(4ˆi+2ˆj)m. The position of centre of mass is
View Solution