What is the torque acting on a plane coil of "n" turns carrying a current "i" and having an area A, when placed in a constant magnetic field B?
Number of turns = n, Current = i, Area of coil = A, Magnetic field = B.
Torque on a current carrying coil in a magnetic field τ=ni(¯¯¯Aׯ¯¯B)=niABsinθ.
Topper's Solved these Questions
- MODEL PAPER 12BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - MODEL PAPER 12EXERCISE - SECTION - B
8 Videos
- MODEL PAPER 12BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - MODEL PAPER 12EXERCISE - SECTION - C
3 Videos
- MODEL PAPER 11BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - MODEL PAPER 11EXERCISE - SECTION -C
3 Videos
- MODEL PAPER 3BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - MODEL PAPER 3EXERCISE - SECTION - C
4 Videos
Similar Questions
To double the torque acting on a coil of n-turns, when placed in a magnetic field
View SolutionCalculate the torque on a 200 turns rectangular coil of length 20cm and breadth 10cm carrying a current of 10A, when placed in a magnetic field. The plane of the coil is making an angle of 60∘ with a magnetic field of 4T.
View Solution
Knowledge Check
To double the torque acting on a rectangular coil of n turns, when placed in a magnetic field-
AArea of the coil and the magnetic induction should be doubled.BArea and current through the coil should be doubled.COnly area of coil should be doubled.DNumber of turns are to be halved.A coil having N turns carry a current I as shown in the figure. The magnetic field intensity at point P is
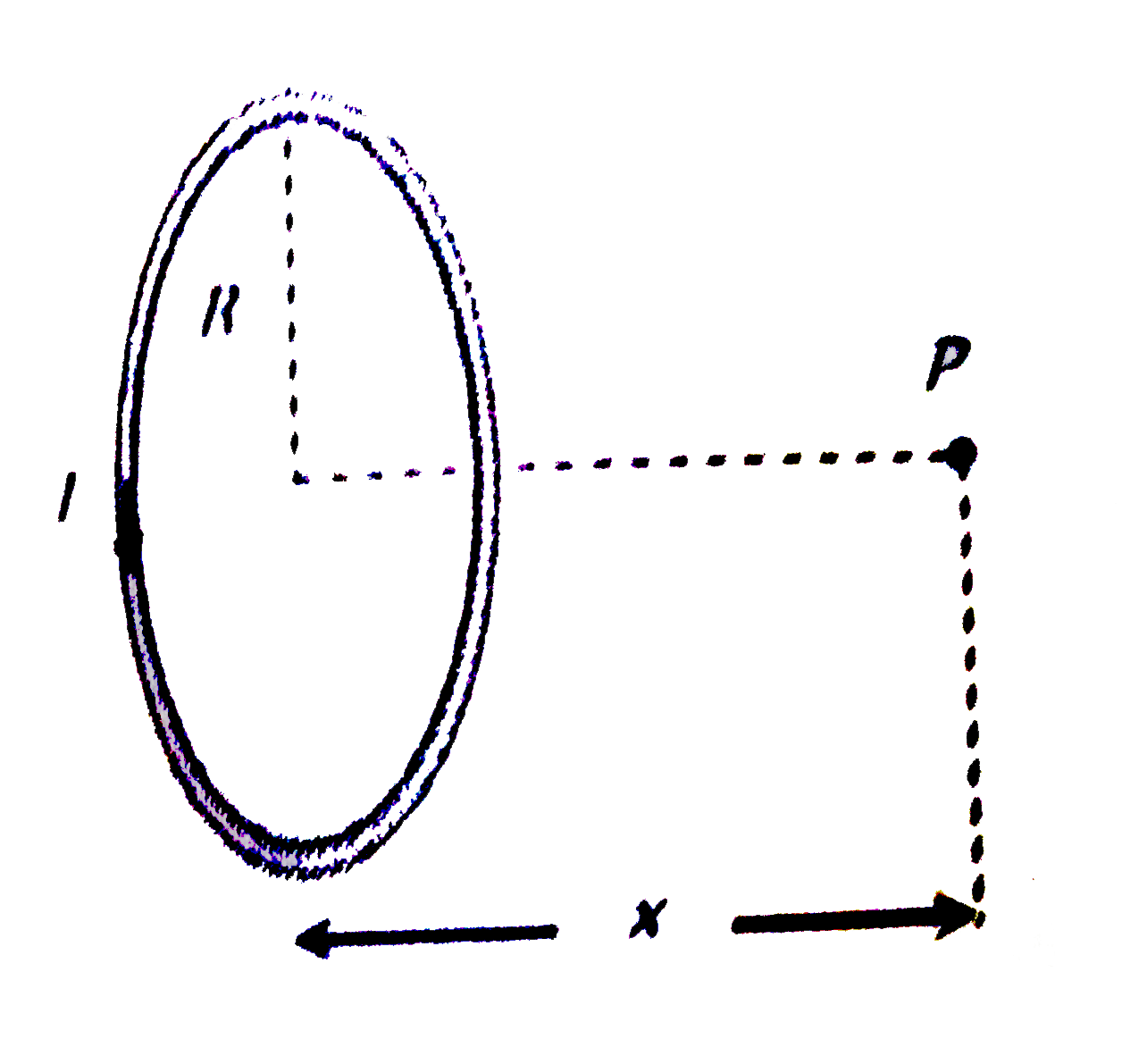 Aμ0NIR22(R2+x2)3/2Bμ0NI2RCμ0NIR2(R+x)2DZero
Aμ0NIR22(R2+x2)3/2Bμ0NI2RCμ0NIR2(R+x)2DZeroThe expression for the torque acting on a coil having area of crosssection A, number of turns n, placed in a magnetic field of strength B, making an angle θ with the normal to the plane of the coil, when a current i is flowing in it, will be
AniABtanθBniABcosθCniABsinθDniAB
What is the value of net force acting on a current carrying (i) rectangular coil and (ii) circular coil of same area placed in a uniform magnetic field? What will be the torque acting in each case?
View SolutionWhat is the magnitude of torque which acts on a coil carrying current placed in a uniform radial magnetic field?
View SolutionThe torque acting on a rectangular loop having area A carrying current i and placed in a magnetic field Bî, with which the loop makes an angle o is given by
View SolutionA coil having N turns carry a current I as shown in the figure. The magnetic field intensity at point P is
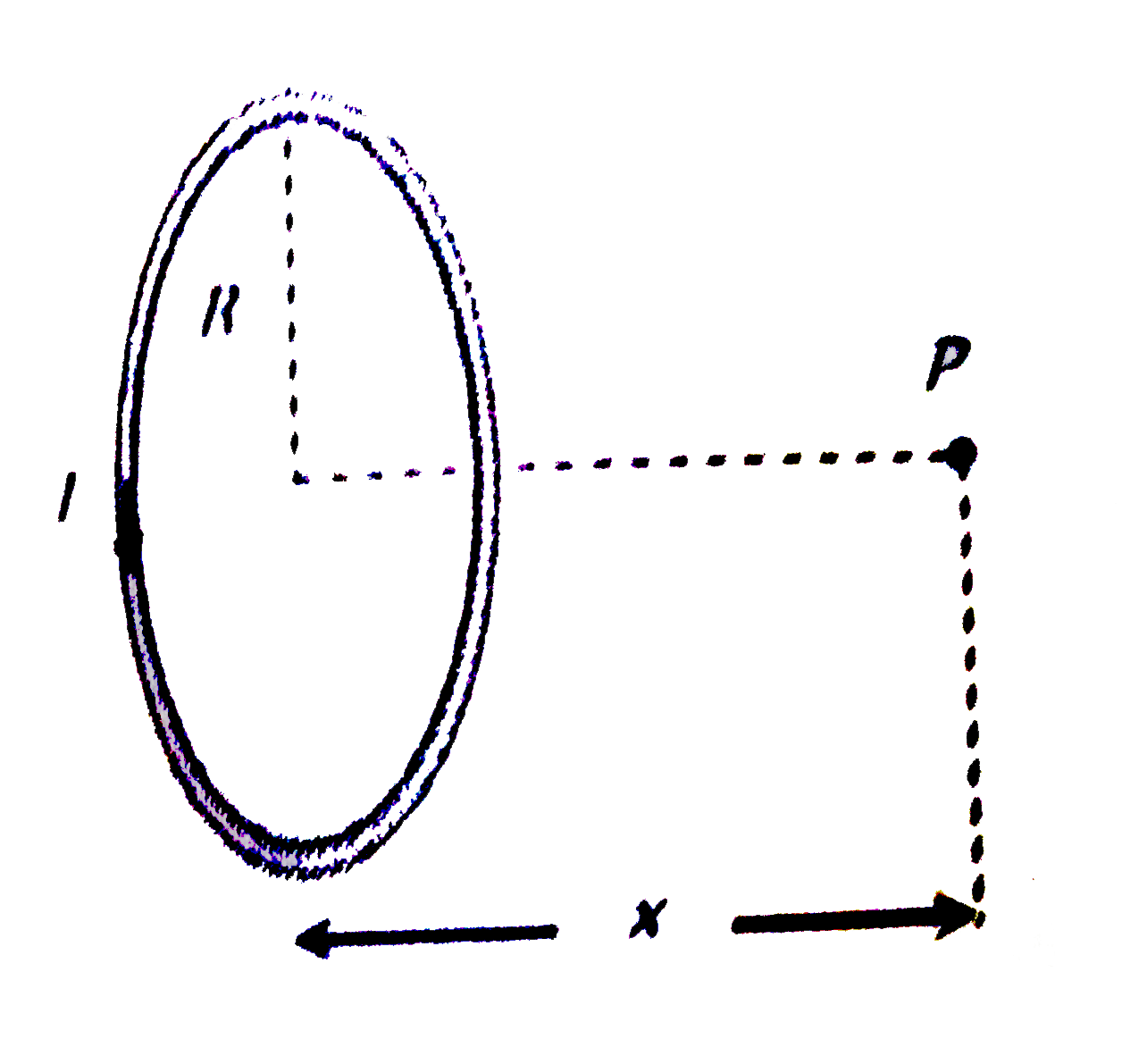
View Solution(a) Derive the expression for the torque acting on a current carrying placed in a magnetic field.
(b) Explain the significance of a radial magnetic when current carrying coil is kept in it.
View Solution
