A whistling train approaches a junction. An observer standing at juction observes the frequency to be and of the approaching and the receding train respectively. Find the speed of the train (speed of sound )
The correct Answer is:30
To solve the problem of finding the speed of the train using the observed frequencies of the whistling train, we can use the Doppler effect equations for sound. Here’s a step-by-step solution:
Step 1: Understand the Doppler Effect
The Doppler effect describes how the frequency of sound changes for an observer moving relative to the source of the sound. When the source approaches the observer, the frequency increases, and when it recedes, the frequency decreases.
Step 2: Write the Doppler Effect Equations
For a source moving towards a stationary observer, the apparent frequency f1 is given by:
f1=vv−vsf0
For a source moving away from a stationary observer, the apparent frequency f2 is given by:
f2=vv+vsf0
Where:
- f0 is the actual frequency of the source.
- v is the speed of sound (300 m/s).
- vs is the speed of the source (train).
Step 3: Set Up the Equations
From the problem, we have:
- f1=2.2kHz=2200Hz (approaching)
- f2=1.8kHz=1800Hz (receding)
Using the equations:
1. For the approaching train:
2200=300300−vsf0(1)
2. For the receding train:
1800=300300+vsf0(2)
Step 4: Divide the Two Equations
Dividing equation (1) by equation (2):
22001800=300/(300−vs)300/(300+vs)
This simplifies to:
22001800=300+vs300−vs
Calculating the left side:
22001800=119
Thus, we have:
119=300+vs300−vs
Step 5: Cross Multiply and Solve for vs
Cross multiplying gives:
11(300−vs)=9(300+vs)
Expanding both sides:
3300−11vs=2700+9vs
Rearranging gives:
3300−2700=11vs+9vs
600=20vs
Thus, solving for vs:
vs=60020=30m/s
Final Answer
The speed of the train is 30m/s.
---
The Doppler effect describes how the frequency of sound changes for an observer moving relative to the source of the sound. When the source approaches the observer, the frequency increases, and when it recedes, the frequency decreases.
For a source moving towards a stationary observer, the apparent frequency f1 is given by:
f1=vv−vsf0
For a source moving away from a stationary observer, the apparent frequency f2 is given by:
f2=vv+vsf0
Where:
- f0 is the actual frequency of the source.
- v is the speed of sound (300 m/s).
- vs is the speed of the source (train).
From the problem, we have:
- f1=2.2kHz=2200Hz (approaching)
- f2=1.8kHz=1800Hz (receding)
1. For the approaching train:
2200=300300−vsf0(1)
2. For the receding train:
1800=300300+vsf0(2)
Dividing equation (1) by equation (2):
22001800=300/(300−vs)300/(300+vs)
This simplifies to:
22001800=300+vs300−vs
Calculating the left side:
22001800=119
Thus, we have:
119=300+vs300−vs
Cross multiplying gives:
11(300−vs)=9(300+vs)
Expanding both sides:
3300−11vs=2700+9vs
Rearranging gives:
3300−2700=11vs+9vs
600=20vs
Thus, solving for vs:
vs=60020=30m/s
The speed of the train is 30m/s.
Topper's Solved these Questions
- WAVE MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - WAVE MOTIONEXERCISE - JEE ADVANCED ARCHIVE LEVEL 2 (FILL IN THE BLANKS)
17 Videos
- WAVE MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - WAVE MOTIONEXERCISE - JEE ADVANCED ARCHIVE LEVEL 2 (TRUE FALSE TYPE)
4 Videos
- WAVE MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - WAVE MOTIONEXERCISE - JEE ADVANCED ARCHIVE LEVEL 2 (MATRIX MATCH TYPE)
3 Videos
- UNITS, MEASUREMENTS & ERRORSBOOK - VMC MODULES ENGLISHCHAPTER - UNITS, MEASUREMENTS & ERRORSEXERCISE - IN - CHAPTER EXERCISE - B
10 Videos
- WORK ENERGY AND POWER BOOK - VMC MODULES ENGLISHCHAPTER - WORK ENERGY AND POWER EXERCISE - IMPECCABLE
54 Videos
Similar Questions
An observer standing on a railway crossing receives frequencies 2.2 kHz and 1.8 kHz when the tran approaches and recedes from the observer. Find the velocity of the train (speed of sound in air is 300 m/s).
View SolutionThe ratio of the apparent frequencies of a car when approaching and receding a stationary observer is 11:9 What is the speed of the car, if the velocity of sound in air is 330 m/s?
View SolutionA train 180 m long crosses a standing man in 12 seconds . Find the speed of the train in km per hour .
View Solution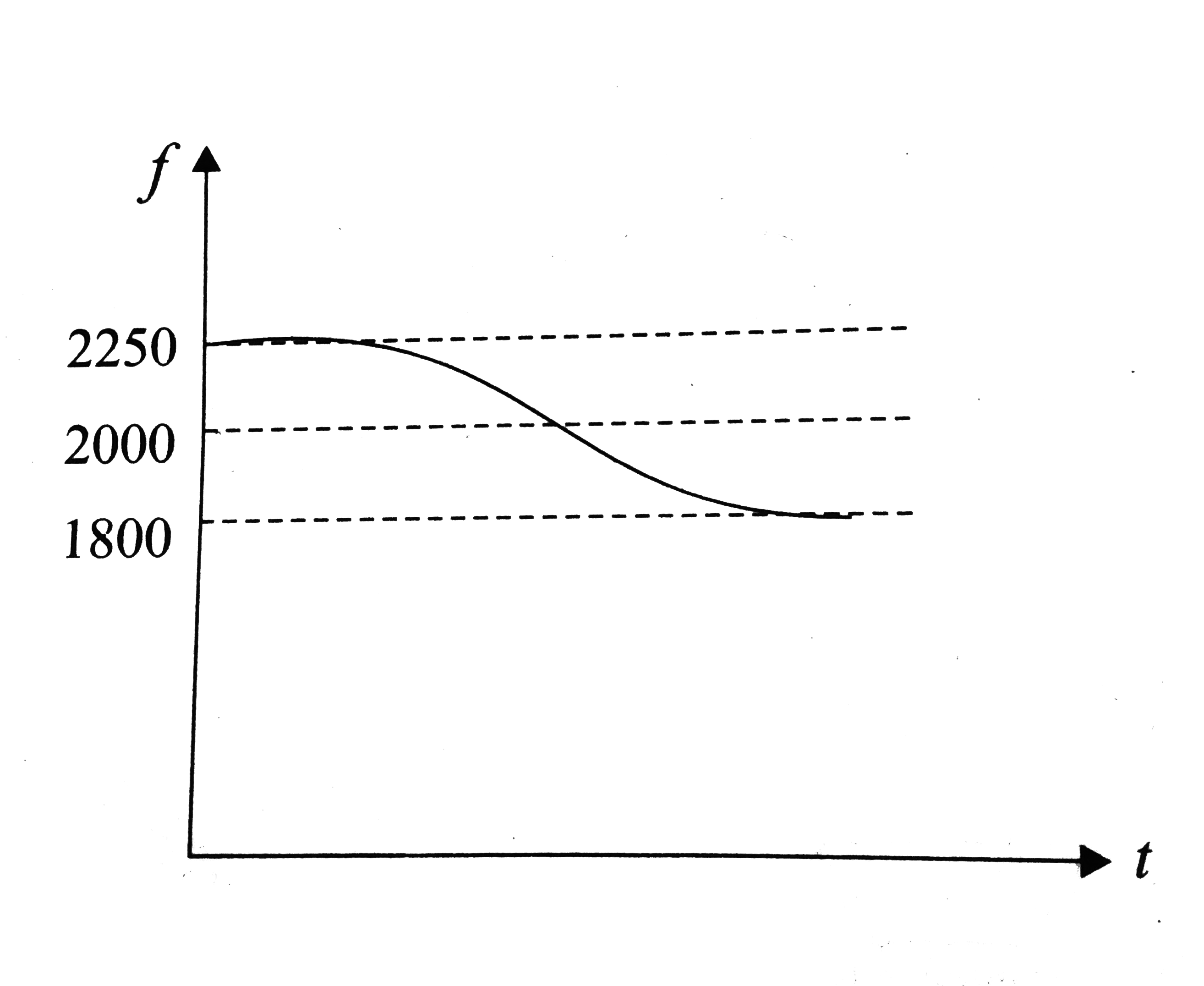
A statinary observer receives a sound of frequency 2000 Hz. The variation of apparent frequency and time is shown. Find the speed of source, if velocity of sound is 300ms
View SolutionAn engine giving off whistle is moving towards a stationary observer with 50m/s speed. What will be the ratio of the frequencies of the whistle heard when engine is approaching and receding from the observer? (speed of sound = 350 m/s)
View SolutionA stationary source of sound is emitting sound of frequency 500Hz. Two observers A and B lying on the same line as the source, observe frequencies 480Hz and 530Hz respectively. The velocity of A and B respectively are (in m/s), speed of sound =300m/s.
View SolutionThe frequency of the whistle of a train is observed to drop from 280 Hz to 260 Hz as the train moves away from a stationary listerner on the platform. Calculate the speed of the train, if speed of sound in air is 340 m/s.
View SolutionTwo trains A and B approach a station from opposite sides, sounding their whistles. A stationary observer on the platform hears no beats. If the velocities of A and B are 15 m/s and 30 m/s respectively and the real frequency of the whistle of B is 600 Hz, find the real frequency of the whistle of A. (Velocity of sound = 330 m/s)
View SolutionA train running at 108 km/hr towards east whistles at a frequency of 800 Hz. The frequencies heard by a passenger sitting in the train and a person standing near the track whom the train has just passed (Speed of Sound =330 m/s)
View SolutionA man standing on a platform observes that the frequency of the sound of a whistle emitted by a train drops by 140 Hz. If the velocity of sound in air is 330 m/s and the speed of the train is 70 m/s, the frequency of the whistle is
View Solution
