Consider four equal charges q1,q2,q3andq4=q=+1μC located at four different points on a circle of radius 1m, as shown in the figure. Calculate the total force acting on the charge q1 due to all the other charges.
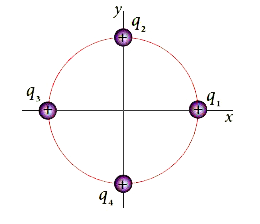
According to the superposition principle, the total electrostatic force on charge q1 is the vector sum of the forces due to the other charges,
→Ftot1=→F12+→F13+→F14
The following diagram shows the direction of each force on the charge q1.
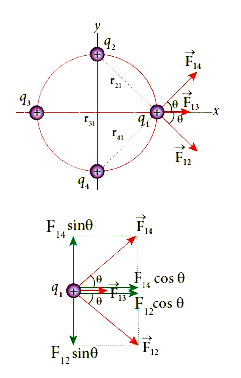
The charges q2andq4 are equip-distant from q1. As a result the strengths (magnitude) of the forces →F12and→F14 are the same even though their directions are different. Therefore the vectors representing these two forces are drawn with equal lengths. the charge q3 is located farther compared to q2andq4. Since the strength of the electrostatic force decreases as distance increases, the strength of the force →F13 is lesser than that of forces →F12and→F14. Hence the vector representing the force →F13 is drawn with smaller length compared to that for forces →F12and→F14.
F13=2.25×10−3N
F12=kq2r221=F14=9×109×10−222
4.5×10−3N
From the figure, the angle θ=45∘. In terms of the components, we have
→F12=F12cosθˆi−F12sinθˆj
=4.5×10−3×1√2ˆi−4.5×10−3×1√2ˆj
→F13=F13ˆi=2.25×10−3Nˆi
→F14=F14cosθˆi+F14sinθˆj
=4.5×10−3×1√2ˆi+4.5×10−3×1√2ˆj
Then the total force on q1 is,
→Ftot1=(F12cosθˆi−F12sinθˆj)+F13ˆi
+(F14cosθˆi+F14sinθˆj)
→Ftot1=(F12cosθ+F13+F14cosθ)ˆi
+(−F12sinθ+F14sinθ)ˆj
Since F12=F14, the jth component is zero. Hence we have
→Ftot1=(F12cosθ+F13+F14cosθ)ˆi
substituting the values in the above equation,
=(4.5√2+2.25+4.5√2)ˆi=(4.5√2+2.25)ˆi
→Ftot1=8.61×10−3Nˆi
The resultant force is along the positive x axis.
Topper's Solved these Questions
- ELECTROSTATICSBook:NCERT TAMILChapter:ELECTROSTATICSExercise:EVALUATION (Multiple choice questions)
Explore 15 Videos
- ELECTROSTATICSBook:NCERT TAMILChapter:ELECTROSTATICSExercise:Exercises
Explore 23 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:NCERT TAMILChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:ADDITIONAL EXERCISES
Explore 1 Video
- MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENTBook:NCERT TAMILChapter:MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENTExercise:EVALUATION (IV. Numerical problems)
Explore 10 Videos
Similar Questions
Four point charges Q.q Q and q are placed at the corners of a square side 'a' as shown in the figures.

Find the resultant electric force on a charge Q,
View SolutionFour point charges Q , q Q and q are placed at the corners of a square of side 'a' as shown in the Fig. Find the
resultant electric force on a charge Q
View Solution
Knowledge Check
The value of charge q1,q2andq3 as shown in the figure are
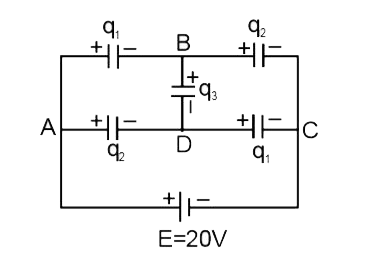 Aq1=32μC,q2=24μC,q3=−8μCBq1=48μc,q2=16μC,q3=+8μCCq1=32μC,q2=24μC,q3=+8μCDq1=3μC,q2=4μC,q3=+2μC
Aq1=32μC,q2=24μC,q3=−8μCBq1=48μc,q2=16μC,q3=+8μCCq1=32μC,q2=24μC,q3=+8μCDq1=3μC,q2=4μC,q3=+2μCTwo positive charges q1andq2 are moving with velocities v1andv2 when they are at points A and B, respectively, as shown in Fig. The magnetic force experienced by charge q1 due to the other charge q2 is
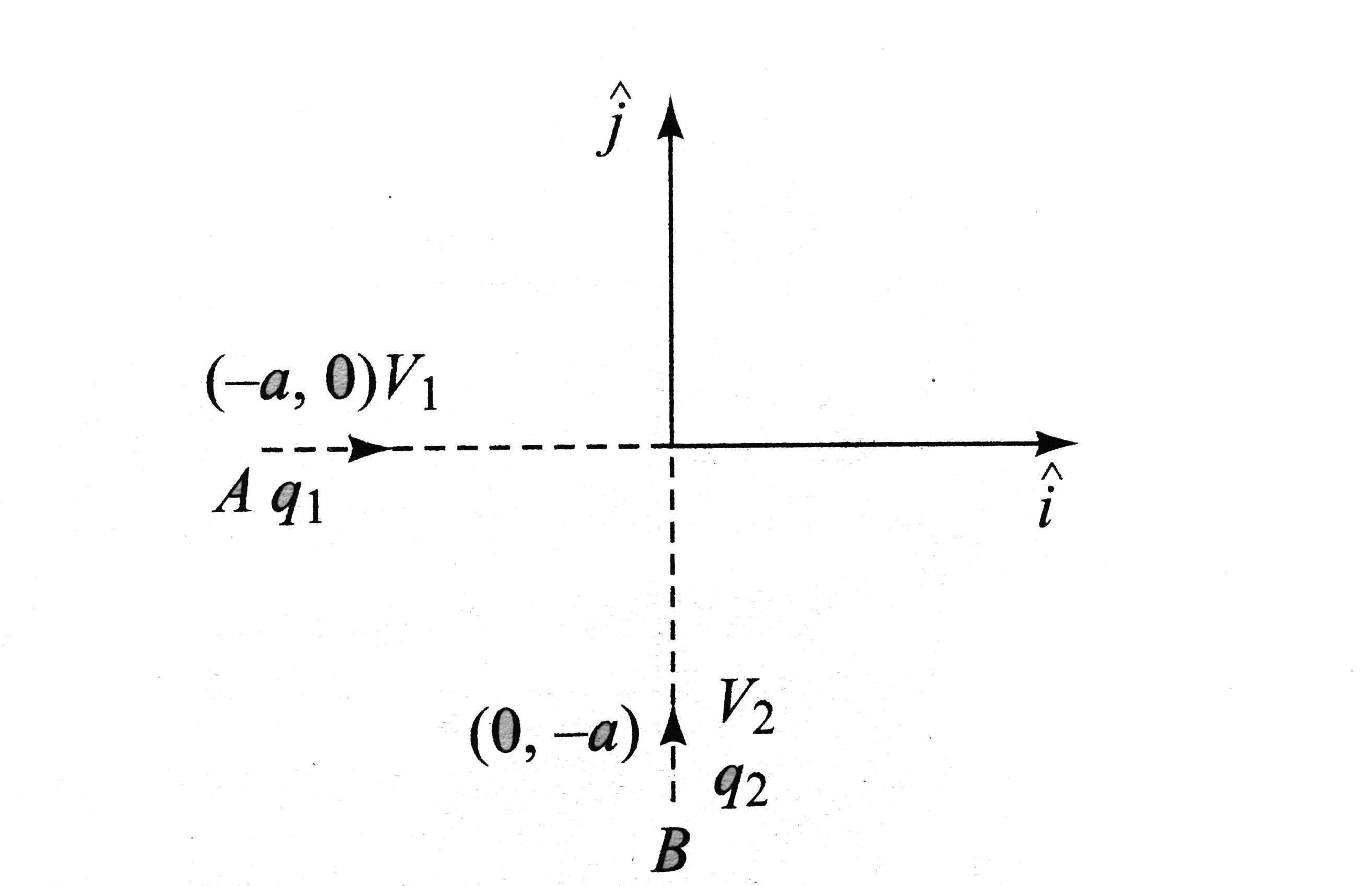 Aμ0q1q2v1v28√2πa2Bμ0q1q2v1v24√2πa2Cμ0q1q2v1v22√2πa2Dμ0q1q2v1v2√2πa2
Aμ0q1q2v1v28√2πa2Bμ0q1q2v1v24√2πa2Cμ0q1q2v1v22√2πa2Dμ0q1q2v1v2√2πa2
Two positive charges q1andq2 are moving with velocities v1andv2 when they are at points A and B, respectively, as shown in Fig. The magnetic force experienced by charge q1 due to the other charge q2 is
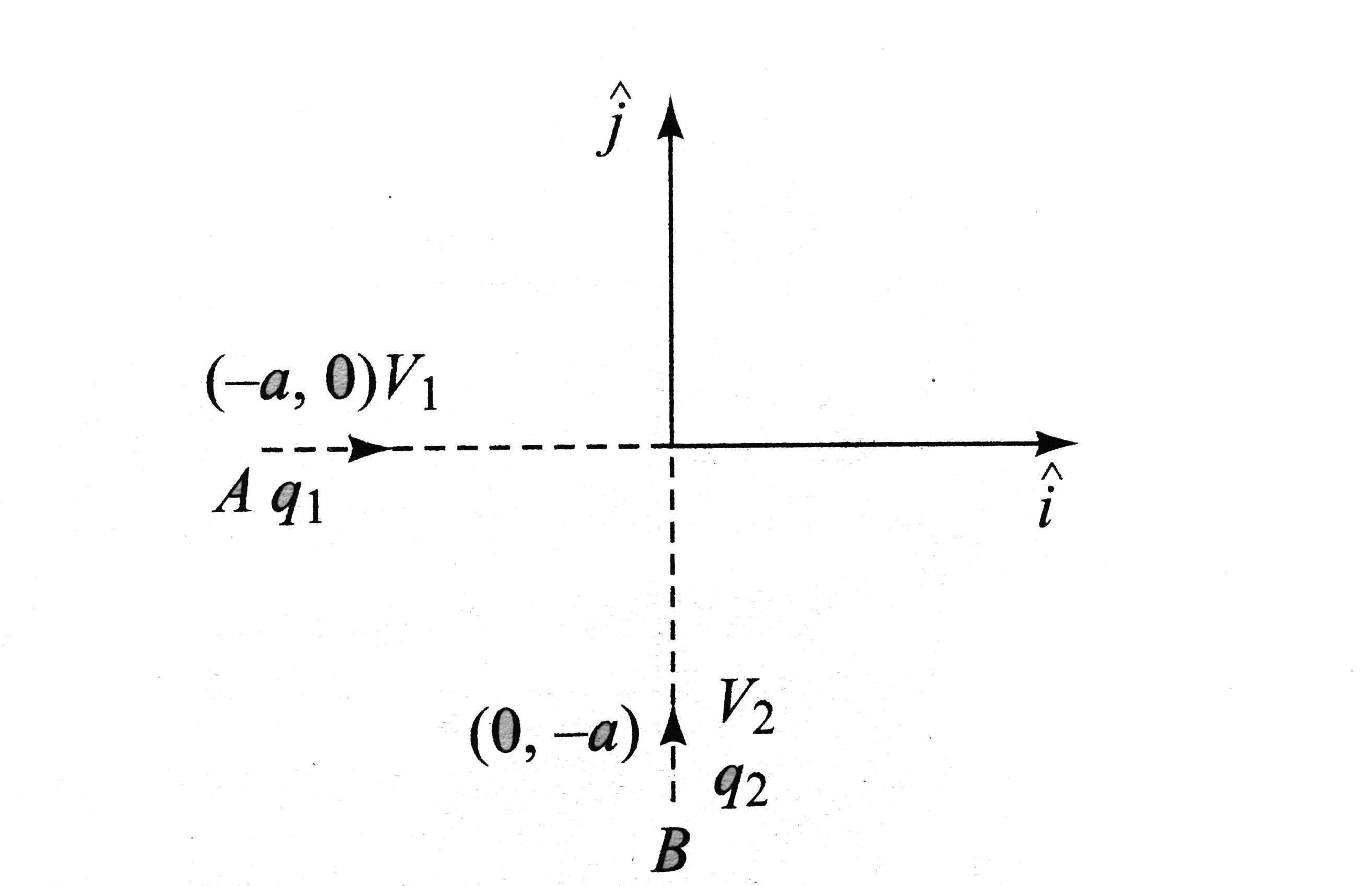
View SolutionFour charges q1=1μC,q2=2μC,q3=−3μCandq4=4μC are kept on the vertices of a square of side 1m. Find the electric potential energy of this system of charges.
View SolutionFour charges q1=1μC,q2=2μC,q3=−3μCandq4=4μC are kept on the vertices of a square of side 1m. Find the electric potential energy of this system of charges.

View SolutionA thin metallic spherical shell contains a charge Q on it. A point charge q is placed at the center of the shell and another charge q1 is placed outside it as shown in the figure. All the three charges are positive. Find the force on the charge

a. at centre due to all charges.
b. at center due to shell.
View SolutionA thin metallic spherical shell contains a charge Q on it. A point charge q is placed at the center of the shell and another charge q1 is placed outside it as shown in the figure. All the three charges are positive. Find the force on the charge

a. at centre due to all charges.
b. at center due to shell.
View SolutionThree charges q1=1μC,q2=2μC and q3=3μC are placed on the vertices of an equilateral triangle of side 1.0 m. Find the net electric force acting on charge q1

View Solution
