A block of mass m and positive charge q is placed on an insulated frictionless inclined plane as shown in the figure. A uniform electric field E is applied parallel to the inclined surface such that the block is at rest. Calculate the magnitude of the electric field E.
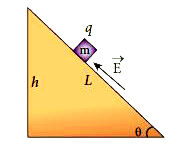
There are three forces that acts on the mass m:
(i) The downward gravitational force exerted by the Earth (mg)
(ii) The normal force exerted by the inclined surface (N)
(iii) The Coulomb force given by uniform electric field (qE)
The free body diagram for the mass m is drawn below.

A convenient inertial coordinate system is located in the inclined surface as shown in the figure. The mass m has zero net acceleration both in x and y-direction.
Along x-direction, applying Newton’s second law, we have
or,
Note that the magnitude of the electric field is directly proportional to the mass m and inversely proportional to the charge q. It implies that, if the mass is increased by keeping the charge constant, then a strong electric field is required to stop the object from sliding. If the charge is increased by keeping the mass constant, then a weak electric field is sufficient to stop the mass from sliding down the plane.
The electric field also can be expressed in terms of height and the length of the inclined surface of the plane.
Topper's Solved these Questions
- ELECTROSTATICSBook:NCERT TAMILChapter:ELECTROSTATICSExercise:EVALUATION (Multiple choice questions)
Explore 15 Videos
- ELECTROSTATICSBook:NCERT TAMILChapter:ELECTROSTATICSExercise:Exercises
Explore 23 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:NCERT TAMILChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:ADDITIONAL EXERCISES
Explore 1 Video
- MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENTBook:NCERT TAMILChapter:MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENTExercise:EVALUATION (IV. Numerical problems)
Explore 10 Videos
Similar Questions
A block of mass 'm' is released on the top of a frictionless incline as shown in the figure. The time period of the oscillation of the block is

View SolutionA block having mass 'm' and charge q is resting on a frictionless plane at distance L from the wall as shown in fig.Discuss the motion of the block when a uniform electric field E is applied horizontally towards the wall assuming that collision of the block with the wall is perfectly elastic.
View Solution
Knowledge Check
Two blocks each of mass M are resting on a frictionless inclined plane as shown in fig then:
 Athe block A moves down the planeBthe block B moves down the planeCboth the blocks remain at restDboth the blocks move down the plane
Athe block A moves down the planeBthe block B moves down the planeCboth the blocks remain at restDboth the blocks move down the planeTwo blocks each of mass M are resting on a frictionless inclined plane as shown in fig then:
 AThe block A moves down the planeBThe block B moves down the plane.CBoth the blocks remain at restDBoth the blocks move down the plane.
AThe block A moves down the planeBThe block B moves down the plane.CBoth the blocks remain at restDBoth the blocks move down the plane.A block of mass 'm' is released on the top of a frictionless incline as shown in the figure. The time period of the oscillation of the block is
 A2π√mK+√2LsinθgB2π√mK+√2(L−l)gsinθC2π√(L−l)gsinθ+√mKDnone of these
A2π√mK+√2LsinθgB2π√mK+√2(L−l)gsinθC2π√(L−l)gsinθ+√mKDnone of these
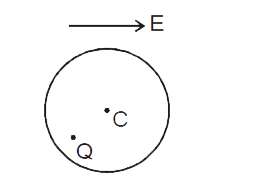
A positive point charge Q is kept (as shown in the figure) inside a neutral conducting shell whose centre is at C. An external uniform electric field E is applied. Then :
View SolutionA block (mass = M kg) is placed on a rough inclined plane. A force F is applied parallel to the inclined (as shown in figure) such that it just starts moving upward. The value of F is
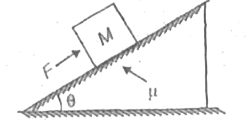
View SolutionA block (mass = M kg) is placed on a rough inclined plane. A force F is applied parallel to the inclined (as shown in figure) such that it just starts moving upward. The value of F is

View SolutionA block of mass m & charge q is released on a long smooth inclined plane magnetic field B is constant, unifrom, horizontal and parallel to surface a shown Find the time from start when block loses contact with the surface
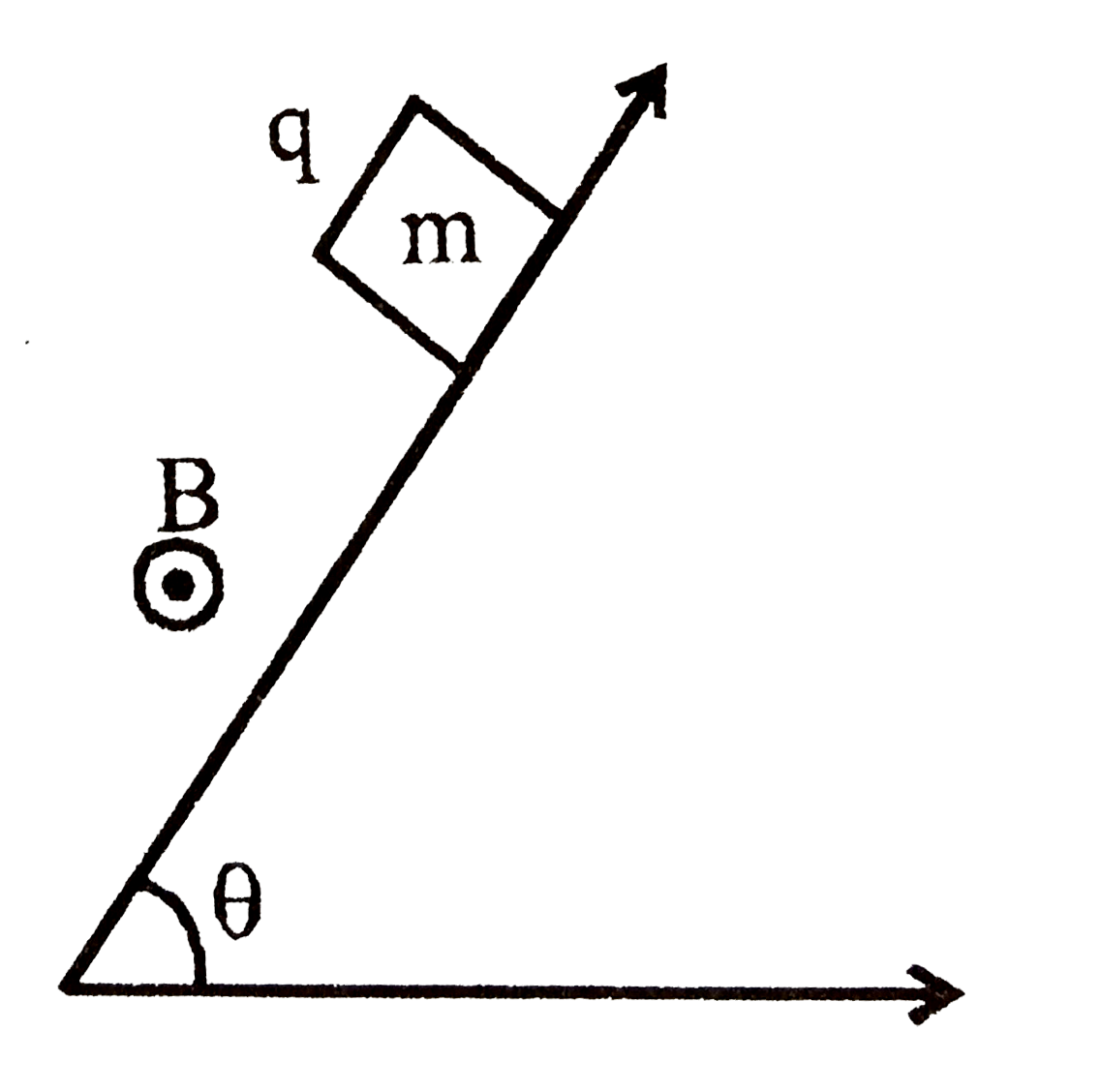 .
.
View SolutionA block of mass m & charge q is released on a long smooth inclined plane magnetic field B is constant, unifrom, horizontal and parallel to surface a shown Find the time from start when block loses contact with the surface
 .
.
View Solution
