Four charges are arranged at the corners of the square PQRS of side a as shown in the figure.
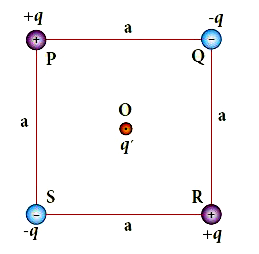
Suppose a charge q′ is brought to the center of the square, by keeping the four charges fixed at the corners, how much extra work is required for this?
Work required to bring the charge q′ to the center of the square = q′ × potential at the center point O due to all the four charges in the four corners
The potential created by the two +q charges are canceled by the potential created by the -q charges which are located in the opposite corners. Therefore the net electric potential at the center O due to all the charges in the corners is zero.
Hence no work is required to bring any charge to the point O. Physically this implies that if any charge q′ when brought close to O, then it moves to the point O without any external force.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - NCERT TAMILCHAPTER - ELECTROSTATICSEXERCISE - EVALUATION (Multiple choice questions)
15 Videos
- ELECTROSTATICSBOOK - NCERT TAMILCHAPTER - ELECTROSTATICSEXERCISE - Exercises
23 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - NCERT TAMILCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ADDITIONAL EXERCISES
1 Video
- MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENTBOOK - NCERT TAMILCHAPTER - MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENTEXERCISE - EVALUATION (IV. Numerical problems)
10 Videos
Similar Questions
Four charges are arranged at the corners of a square ABCD as shown in the figure. The force on the charge kept at the centre O will be:

View SolutionFour point charges are placed at the corners of a square ABCD of side 10 cm, as shown in figure. The force on a charge of 1μC placed at the centre of square is

View Solution
Knowledge Check
Four charges are arranged at the corners of a square ABCD as shown in the figure. The force on the charge kept at the centre O will be:
 AzeroBalong the diagonal ACCalong the diagonal BDDperpendicular to side AB
AzeroBalong the diagonal ACCalong the diagonal BDDperpendicular to side ABFour charges are arranged at the corners of a square ABCD as shown in the figure. The force on the charge kept at the centre O will be:
 Aperpendicular to side ABBalong the diagonal BDCalong the diagonal ACDzero
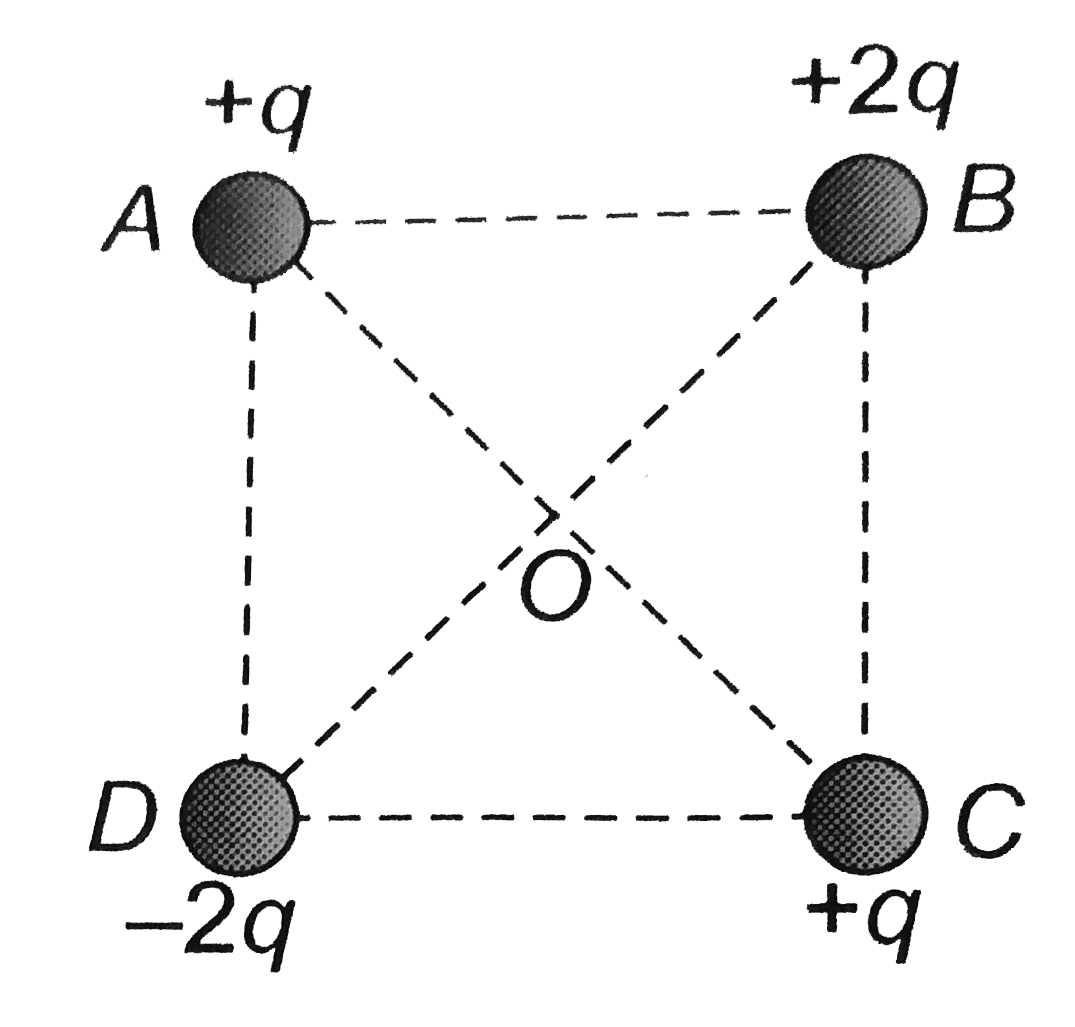
Aperpendicular to side ABBalong the diagonal BDCalong the diagonal ACDzeroFour charges are arranged at the corners of a square ABCD, as shown in the adjoining figure, The force on a positive charge kept at the centre O is
 AZeroBAlong the diagonal ACCAlong the diagonal BDDPerpendicular to side AD
AZeroBAlong the diagonal ACCAlong the diagonal BDDPerpendicular to side AD
Four point charges are placed at the corners of a square ABCD of side 10 cm, as shown in figure. The force on a charge of 1μC placed at the centre of square is

View SolutionThree particles each of mass m are placed at the three corners of an equilateral triangle of side a. The work which should be done to increase the sides of the triangle to 2a is
View SolutionFour charges are arranged at the corners of a square ABCD as shown in the figure. The force on the charge kept at the ccentre O is
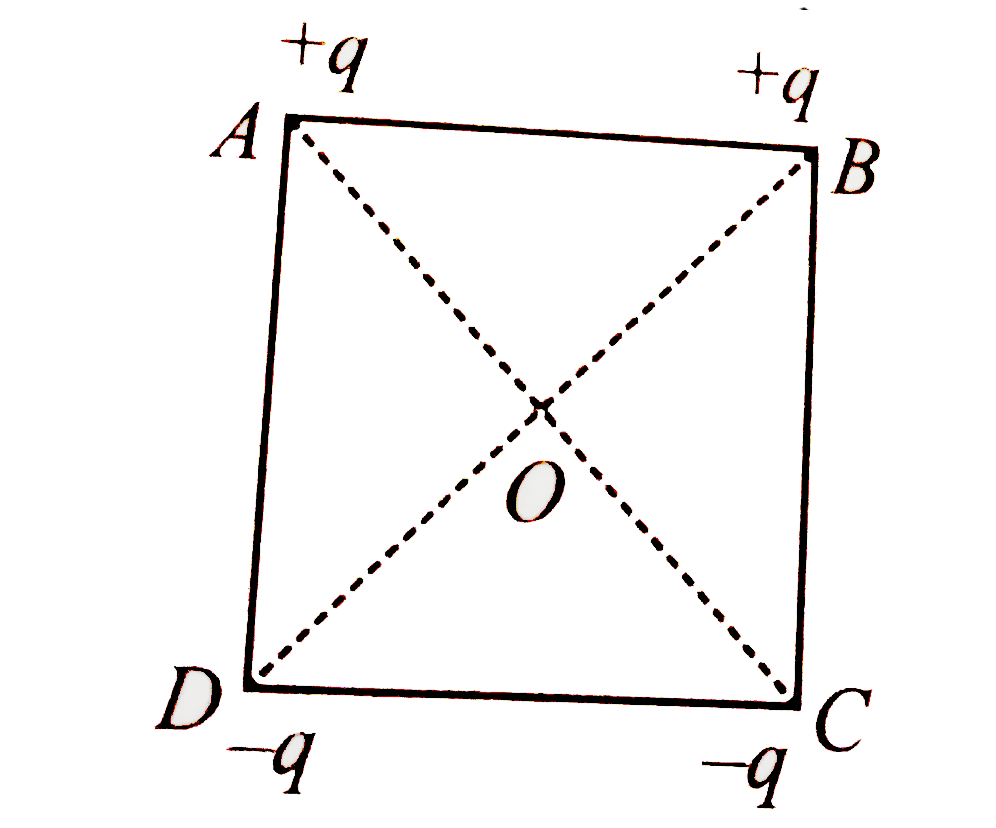
View SolutionFour charges are arranged at the corners of a square ABCD, as shown in the adjoining figure. The force on the charge kept at the centre O is
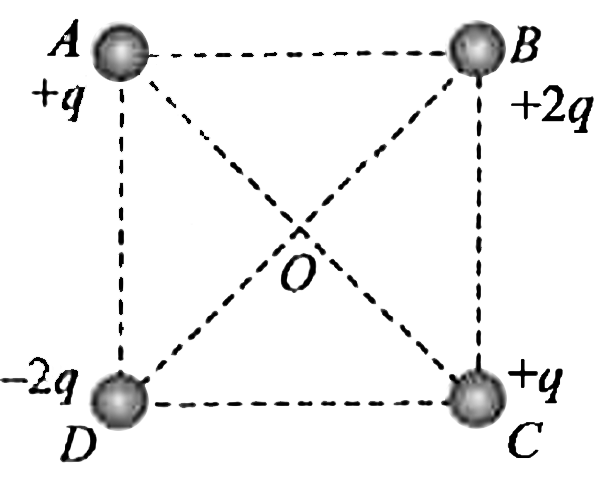
View SolutionFour charges are arranged at the corners of a square ABCD, as shown. The force on a positive charge kept at the centre of the square is

View Solution
