Three particles each of mass m are placed at the three corners of an equilateral triangle of side a. The work which should be done to increase the sides of the triangle to 2a is
(a) Since the work done depends on the final arrangement of the charges, and not on how they are put together, we calculate work needed for one way of putting the charges at A, B, C and D. Suppose, first the charge + q is brought to A, and then the charges – q, + q, and – q are brought to B, C and D, respectively. The total work needed can be calculated in steps:
(i) Work needed to bring charge + q to A when no charge is present elsewhere: this is zero.
(ii) Work needed to bring – q to B when + q is at A. This is given by (charge at B) × (electrostatic potential at B due to charge + q at A)
=−q×(q4πε0d)=−q24πε0d
(iii) Work needed to bring charge +q to C when +q is at A and –q is at B. This is given by (charge at C) × (potential at C due to charges at A and B)
=+q(+q4πε0d√2+−q4πε0d)
=−q24πε0d(1−1√2)
(iv) Work needed to bring –q to D when +q at A,–q at B, and +q at C. This is given by (charge at D) × (potential at D due to charges at A, B and C)
=−q(+q4πε0d+−q4πε0d√2+q4πε0d)
=−q24πε0d(2−1√2)
Add the work done in steps (i), (ii), (iii) and (iv). The total work required is
=−q24πε0d{(0)+(1)(1−1√2)+(2−1√2)}
=−q24πε0d(4−√2)
The work done depends only on the arrangement of the charges, and not how they are assembled. By definition, this is the total electrostatic energy of the charges. (Students may try calculating same work/energy by taking charges in any other order they desire and convince themselves that the energy will remain the same.)
(b) The extra work necessary to bring a charge q0 to the point E when the four charges are at A, B, C and D is q0× (electrostatic potential at E due to the charges at A, B, C and D). The electrostatic potential at E is clearly zero since potential due to A and C is cancelled by that due to B and D. Hence, no work is required to bring any charge to point E.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NCERT ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Exercise
37 Videos
- ELECTROMAGNETIC WAVESBOOK - NCERT ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise
15 Videos
- MAGNETISM AND MATTERBOOK - NCERT ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Exercise
25 Videos
Similar Questions
Three particle of mass m each are placed at the three corners of an equilateral triangle of side a. Find the work which should be done on this system to increase the sides of the triangle to 2a.
View SolutionThree particle of mass m each are placed at the three corners of an equilateral triangle of side a. Find the work which should be done on this system to increase the sides of the triangle to 2a.
View Solution
Knowledge Check
Three point masses each of mass m are placed at the corners of an equilateral triangle of side b. The moment of inertia of the system about an axis coinciding with one side of the triangle is
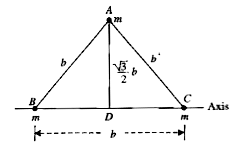 A3mb2Bmb2C(3/4)mb2D(2/3)mb2
A3mb2Bmb2C(3/4)mb2D(2/3)mb2
Three particle of mass m each are placed at the three corners of an equilateral triangle of side a. Find the work which should be done on this system to increase the sides of the triangle to 2a.
View SolutionThree particle of mas m each are placed at the three corners of an equlateral triangle of side a. Find the work which should be done on this system to increase the sides of the triangle to 2a.
View SolutionThree particle each of mass m are placed at the corners of equilateral triangle of side l

Which of the following is/are correct ?
View SolutionThree particles of equal mass 'm' are situated at the vertices of an equilateral triangle of side L. The work done in increasing the side of the triangle to 2L is
View SolutionThree particles each of mass m are kept at vertices of an equilateral triangle of side L. The gravitational field at centre due to these particle is
View SolutionThree equal masses each of mass 'm' are placed at the three-corner of an equilateral triangle of side 'a'
If a fourth particle of equal mass is placed at the centre of triangle, then net force acting on it, is equal to
View SolutionConstruct an equilateral triangle of sides 6 cm each.
View Solution
