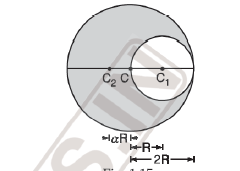
A circular disc of radius R is removed from a bigger circular dise of radius 2 R from one edge of the disc as shown in Fig. The centre of mass of the new disc is from the centre of the bigger disc. Find the value of .
 Solution in Punjabi
Solution in Punjabi
Step by step video & image solution for A circular disc of radius R is removed from a bigger circular dise of radius 2 R from one edge of the disc as shown in Fig. The centre of mass of the new disc is alpha Rfrom the centre of the bigger disc. Find the value of alpha. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- Moment of InertiaBOOK - MODERN PUBLICATIONCHAPTER - Moment of InertiaEXERCISE - Example
323 Videos
- Gravitational potential and potential energyBOOK - MODERN PUBLICATIONCHAPTER - Gravitational potential and potential energyEXERCISE - Exercise
17 Videos
- Motion of SatellitesBOOK - MODERN PUBLICATIONCHAPTER - Motion of SatellitesEXERCISE - Exercise
25 Videos
Similar Questions
The moment of inertia of a thin rod about an axis passing through its centre and perpendicular to its length is 1,200gcm2. If length of the rod is 20 cm, find its moment of inertia about an axis passing through its one end and perpendicular to its length.
View SolutionWhat do you understand by gravitational field?
View SolutionDefine orbital velocity of a satellite. Obtain an expression for orbital velocity of a satellite.
View SolutionA circular disc of radius R is removed from a bigger circular disc of radius 2R such that the cirucmferences of the discs coincide. The centre of mass of the new disc is αR from the center of the bigger disc. The value of α is
View SolutionFrom the circular disc of radius 4R two small discs of radius R are cut off. The centre of mass of the new structure will be at
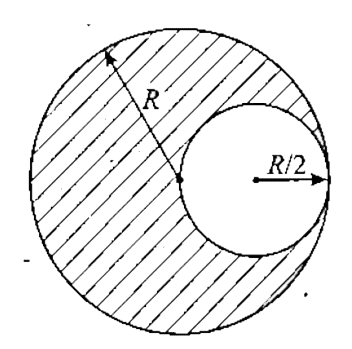
View SolutionFrom a uniform circular dis of radius R , a circular dis of radius R//6 and having centre at a distance R//2 from the centre of the disc is removed. Determine the centre of mass of remaining portion of the disc.
View SolutionA circular disc of radius R is removed from a bigger circular disc of radius 2 R such that the circumferences of the discs coincide. The center of mass of new disc is alpha R from the center of the bigger disc. The value of alpha is
View SolutionA circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumferences of the discs touch. The centre of mass of the new disc is at a distance aR from the centre of the bigger disc. The value of a is
View SolutionA circular disc of radius R is removed from a bigger circular disc of radius 2R, such that the circumference of the disc coincides. The centre of mass of the new disc is αR from the centre of bigger disc. The value of alpha is
View SolutionA circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumference of the discs coincoid . The centre of mass of the new disc is alphaR from the centre of the bigger disc . the value of alpha is
View SolutionA circular disc of radius R is removed from a bigger circular dise of radius such that the circumferences of the discs coincide. The centre of mass of the new disc is alphaR from the centre of the bigger disc. The value of a is:
View SolutionA circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumferences of the disc coincide. The centre of mass of the new disc is αR from the centre of the bigger disc. The value of α is :
View SolutionA circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumferences of the discs touch. The centre of mass of the new disc is at a distance aR from the centre of the bigger disc. The value of a is
View SolutionA circular disc of radius R is removed from a bigger of the discs coincide. The centre of mass of the new disc is ar from the centre of the bigger disc. The value of α is
View SolutionA solid toy is in the form of a hemisphere surmounted by a right circular cone of same radius. The height of the cone is 10 Cm and the radius of the base is 7 cm. Determine the volume of the toy. Also find the area of the coloured sheet required to cover the toy. (Use π=22/7 and √149=12.2)
View SolutionFrom the circular disc of radius 4R two small discs of radius R are cut off. The centre of mass of the new structure will be at

View Solution
