The distance of center of mass from the center of a uniform disc of radius R. if a circular plate is removed from the disc as shown in figure will be (C is centre of complete disc)
R6
R2
3R8
R4
The correct Answer is:B
To solve the problem of finding the distance of the center of mass from the center of a uniform disc after a circular plate is removed, we can follow these steps:
1. Identify the Components:
- Let the radius of the original uniform disc be R.
- When a circular plate of radius r is removed from the disc, we need to consider the center of mass of the remaining part of the disc.
2. Define the Centers:
- Let C be the center of the original disc.
- Let C1 be the center of the removed circular plate.
- Let C2 be the center of mass of the remaining portion of the disc.
3. Mass Consideration:
- Let m1 be the mass of the removed circular plate.
- Let m2 be the mass of the remaining part of the disc.
4. Use the Center of Mass Formula:
- The center of mass of the system can be calculated using the formula:
m1⋅→C1+m2⋅→C2=0
- Rearranging gives:
m2⋅→C2=−m1⋅→C1
- This indicates that the moment of the masses about the center of the original disc is zero.
5. Express the Centers in Terms of Distances:
- If we assume the distance from C to C1 is R (the radius of the disc), then we can express →C1 as R in the direction away from C.
6. Calculate the Center of Mass of the Remaining Portion:
- From the above equation, we can express →C2:
→C2=−m1m2⋅→C1
- Since m1 and m2 are proportional to the areas of the discs, we can say:
m1m2=Area of removed plateArea of remaining disc=πr2π(R2−r2)=r2R2−r2
7. Substituting Values:
- Substitute this ratio back into the equation for →C2:
→C2=−r2R2−r2⋅R
8. Finding the Distance:
- The distance from C to C2 is thus:
d=r2R2−r2⋅R
- For small values of r compared to R, this simplifies to R2.
9. Conclusion:
- Therefore, the distance of the center of mass from the center of the uniform disc after removing the circular plate is R2.
Final Answer:
The distance of the center of mass from the center of the uniform disc is R2.
- Let the radius of the original uniform disc be R.
- When a circular plate of radius r is removed from the disc, we need to consider the center of mass of the remaining part of the disc.
- Let C be the center of the original disc.
- Let C1 be the center of the removed circular plate.
- Let C2 be the center of mass of the remaining portion of the disc.
- Let m1 be the mass of the removed circular plate.
- Let m2 be the mass of the remaining part of the disc.
- The center of mass of the system can be calculated using the formula:
m1⋅→C1+m2⋅→C2=0
- Rearranging gives:
m2⋅→C2=−m1⋅→C1
- This indicates that the moment of the masses about the center of the original disc is zero.
- If we assume the distance from C to C1 is R (the radius of the disc), then we can express →C1 as R in the direction away from C.
- From the above equation, we can express →C2:
→C2=−m1m2⋅→C1
- Since m1 and m2 are proportional to the areas of the discs, we can say:
m1m2=Area of removed plateArea of remaining disc=πr2π(R2−r2)=r2R2−r2
- Substitute this ratio back into the equation for →C2:
→C2=−r2R2−r2⋅R
- The distance from C to C2 is thus:
d=r2R2−r2⋅R
- For small values of r compared to R, this simplifies to R2.
- Therefore, the distance of the center of mass from the center of the uniform disc after removing the circular plate is R2.
The distance of the center of mass from the center of the uniform disc is R2.
Similar Questions
From a uniform disc of radius R, an equilateral triangle of side √3R is cut as shown in the figure. The new position of centre of mass is :

View SolutionFind the centre of mass of a uniform disc of radius a from which a circualr section of radius b has been removed. The centre of hole is at a distance c from the centre of the disc.
View SolutionFind the position of center of mass of the uniform lamina shown in figure, if small disc of radius α2 is cut from disc of radius a.
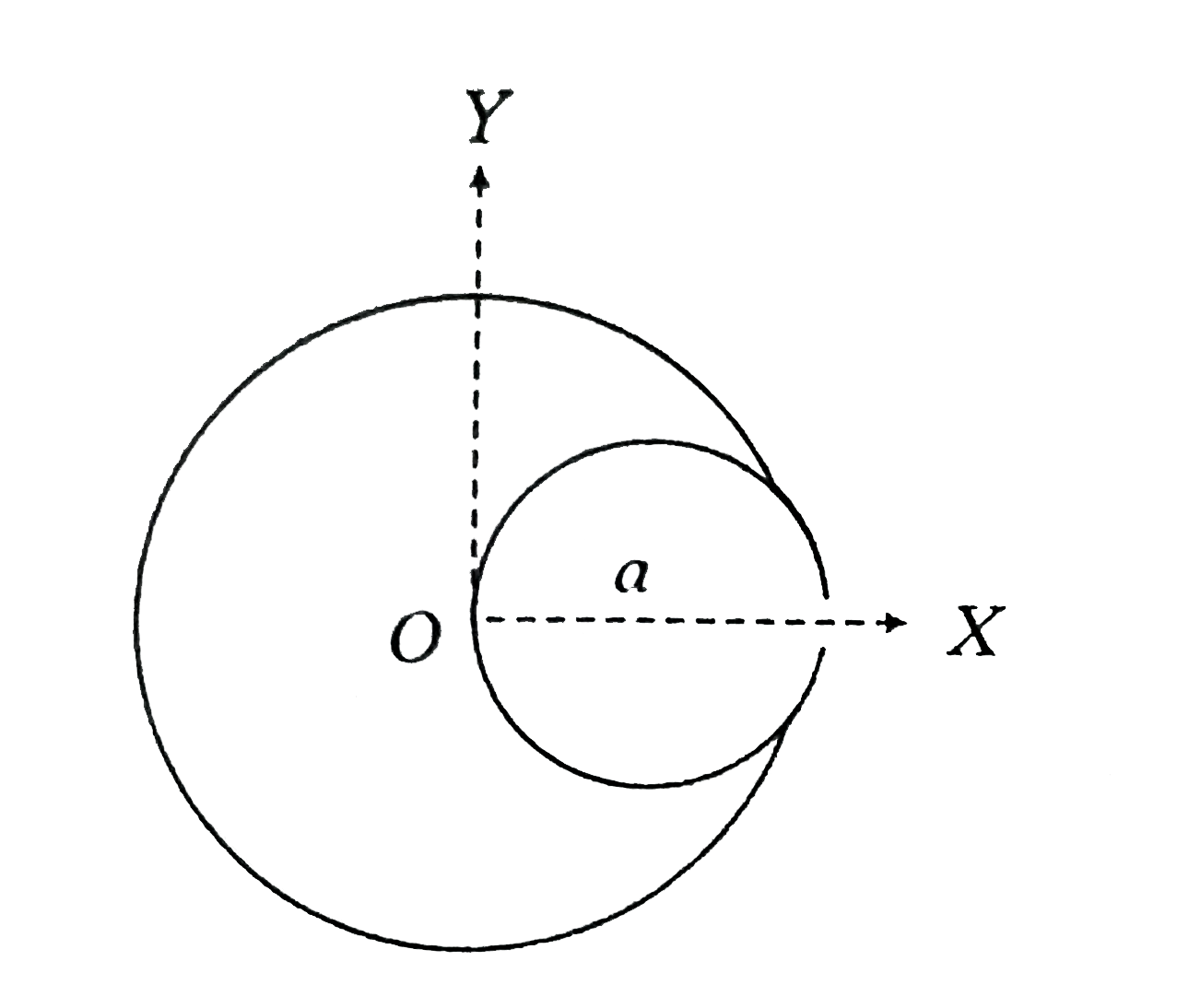
View SolutionA circular metallic disc of radius R has a small circular cavity of radius r as shown in figure. On heating the system

View SolutionThe moment of inertia of a uniform circular disc of radius R and mass M about an axis passing from the edge of the disc and normal to the disc is.
View SolutionA non - conducting disc of radius R is uniformly charged with surface charge density σ. A disc of radius R2 is cut from the disc, as shown in the figure. The electric potential at centre C of large disc will be

View SolutionA uniform disc of mass M and radius R is liffted using a string as shown in the figure. Then choose incorrect option(s),

View SolutionFrom a circular disc of radius R and mass 9 M , a small disc of radius R/3 is removed from the disc. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is

View SolutionA disc of radius r is removed from the centre of a disc of mass M and radius R. The M.I. About the axis through the centre and normal to the plane will be:
View SolutionFind the position of center of mass of the uniform lamina shown in figure, if small disc of radius α2 is cut from disc of radius a.
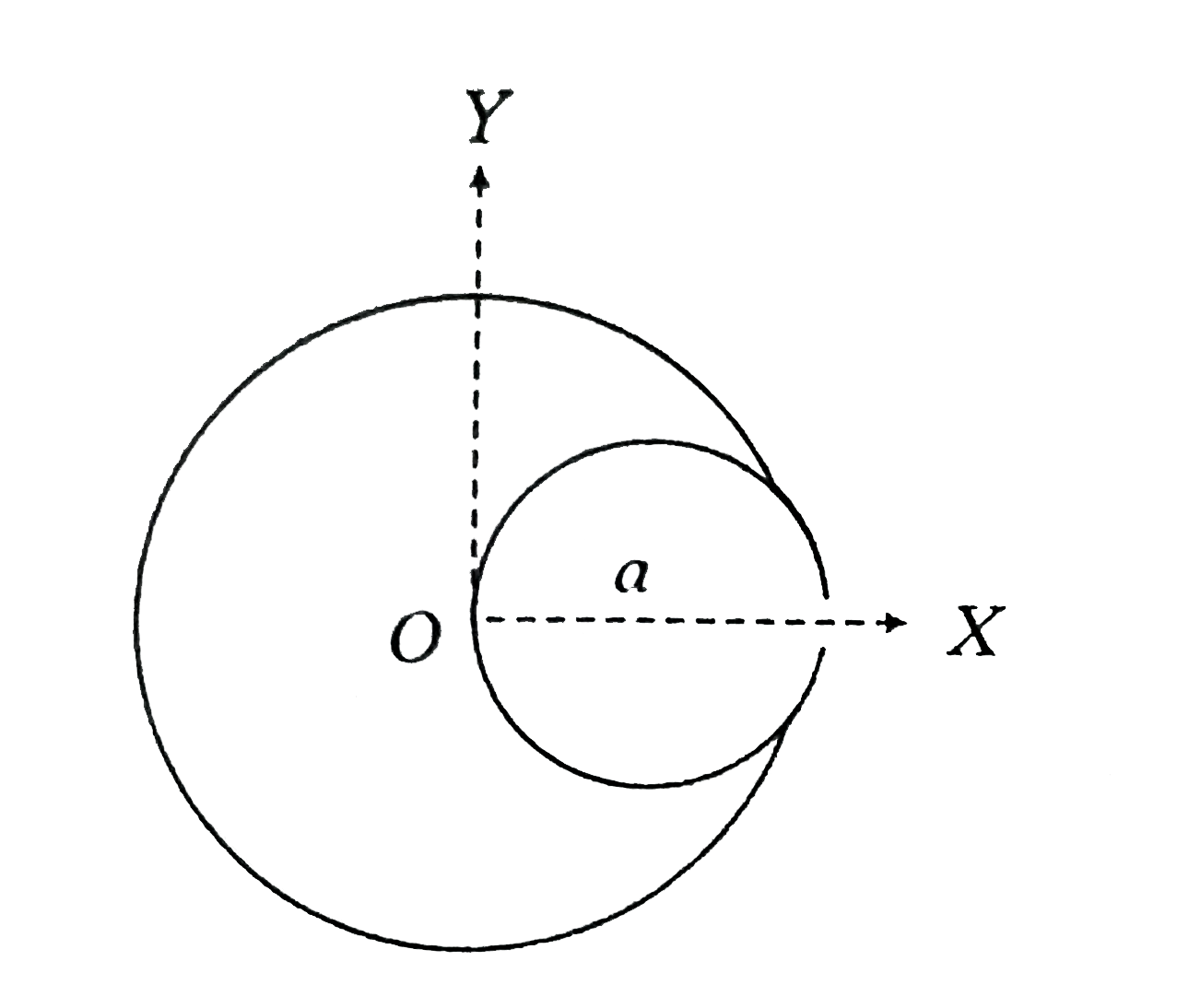
View Solution
