
As shown in the above figure, a loop surrounds three regions of the magnetic field where the magnitude of the magnetic field is decreasing at a constant rate a. Take the area of each region as A. Now find the
∮→E.→dl along the given loop, where →E is the induced electric field.
αA
−αA
3αA
−3αA
The correct Answer is:B
From faraday law of emf, a time varying magnetic field produces electric field according to the following equation: ∮→E.d→l=−dϕdt
also, ϕ=B.A is the magnetic flux assosiated substituting this in the above equation,we get:
⇒∮→E+E.→l=−d(BA)dt
⇒∮→E.d→l=−AdBdt
Here it is given that dBdt=α and now taking the sign of flux according to right hand curl rule we get:
=∮→E.d→l=−[−(−αA)−(−αA)+(−αA)]
⇒∮→E.d→l=−αA
Topper's Solved these Questions
Similar Questions
Figure. shows three rigions of magnetic field each of area A, and in each rigion, magnitude of mqagnetic field decreases rate α. If →E is the induced electric field, then the vlue of the line ∮→E.d→r along the given loop is equal to

View SolutionA uniform but time varying magnetic field is present in a circular region of radius R. The magnetic field is perpendicular and into the plane of the loop and the magnitude of field is increasing at a constant rate α. There is a straight conducting rod of length 2R placed as shown in figure.
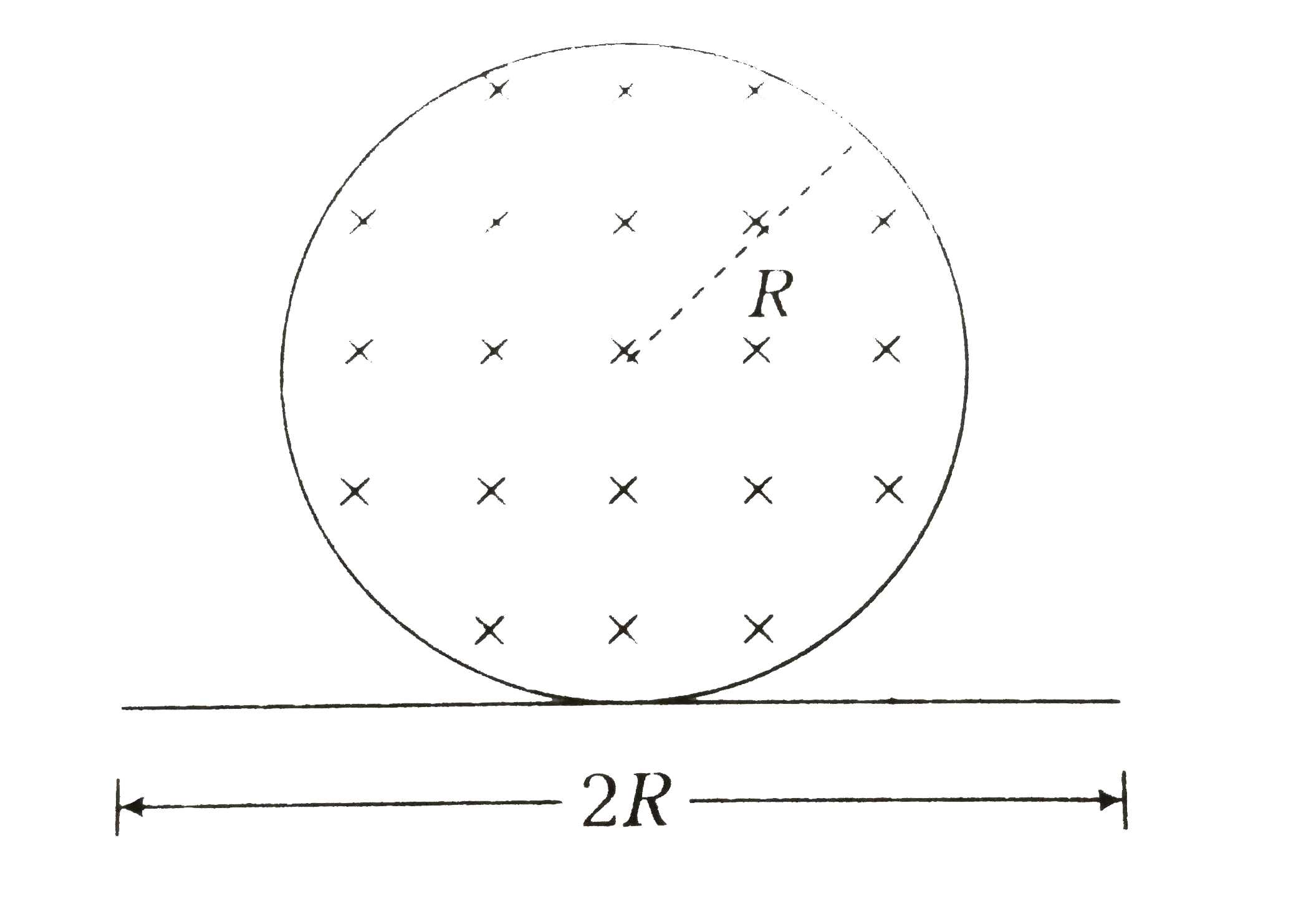
The magnitude of induced emf across the rod is
View Solution
Knowledge Check
Figure. shows three rigions of magnetic field each of area A, and in each rigion, magnitude of mqagnetic field decreases rate α. If →E is the induced electric field, then the vlue of the line ∮→E.d→r along the given loop is equal to
 A(a) αAB(b) −αAC( c) 3αAD(d) −3αA
A(a) αAB(b) −αAC( c) 3αAD(d) −3αAIn a certain region of space the electric potential V is known to be constant. Is the electric field in this region (a) positive (b) zero ,or (c ) negative ?
AAlso constantBPositiveCNegativeDZeroA uniform but time varying magnetic field is present in a circular region of radius R. The magnetic field is perpendicular and into the plane of the loop and the magnitude of field is increasing at a constant rate α. There is a straight conducting rod of length 2R placed as shown in figure.

The magnitude of induced emf across the rod isAπR2αBπR2α2CR2α√2Dπr2α4
An electric field (vec E) and a magnetic field (vec B)exist in a region . The fields are not perpendicular to each other.
View SolutionAn electric field (vec E) and a magnetic field (vec B)exist in a region . The fields are not perpendicular to each other.
View SolutionA wire is bent to form the double loop shown in figure. There is a uniform magnetic field directed into the plane of the loop. If the magnitude of this field is decreasing current will flow from:
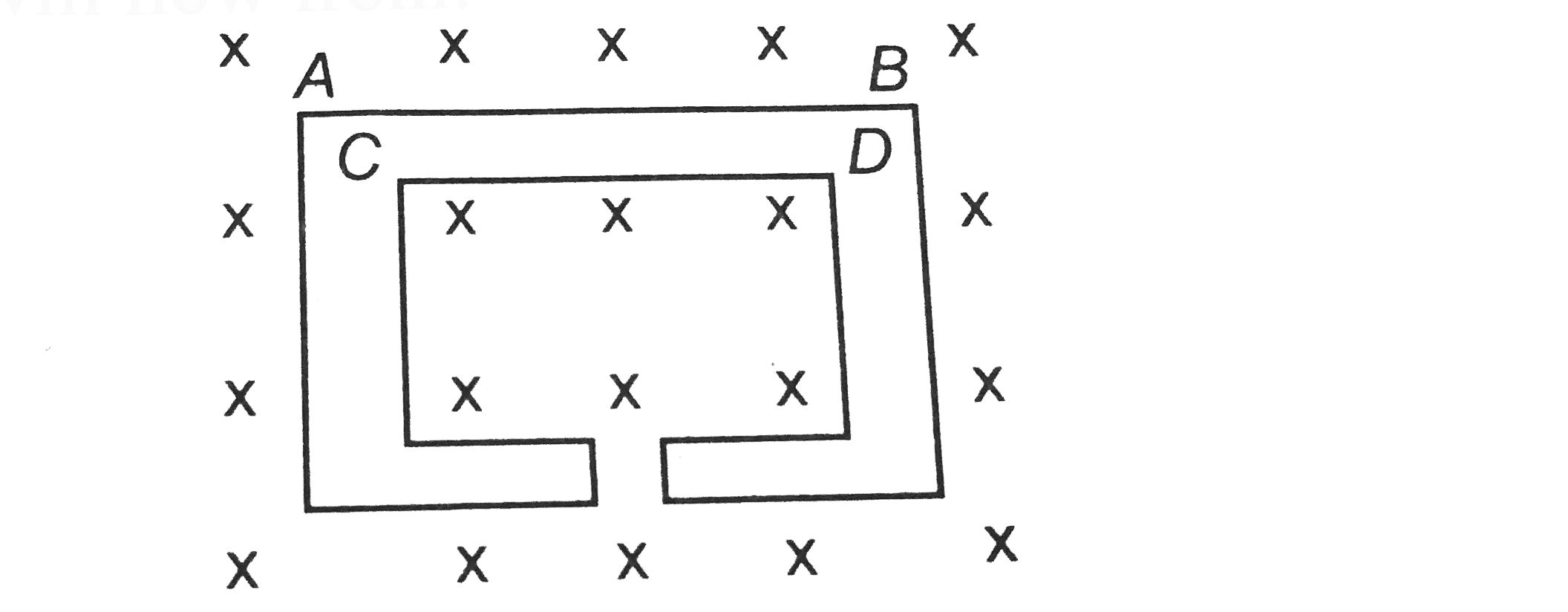
View SolutionA wire is bent to form the double loop shown in figure. There is a uniform magnetic field directed into the plane of the loop. If the magnitude of this field is decreasing current will flow from:

View SolutionA wire is bent to form the double loop shown in figure. There is a uniform magnetic field directed into the plane of the loop. If the magnitude of this field is decreasing, current will flow from:
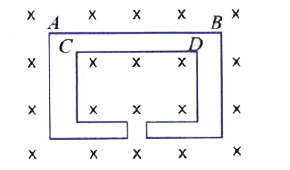
View Solution
