The time period for small vertical oscillations of block of mass m when the masses of the pulleys are negligible and spring constant k1 and k2 is
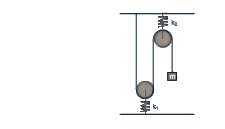
T=4π√m(1k1+1k2)
T=2π√m(1k1+1k2)
T=4π√m(k1+k2)
T=2π√m(k1+k2)
The correct Answer is:A
Topper's Solved these Questions
- OSCILLATIONSBOOK - NCERT TAMILCHAPTER - OSCILLATIONSEXERCISE - EVALUATION(IV. NUMERICAL PROBLEMS)
4 Videos
- OSCILLATIONSBOOK - NCERT TAMILCHAPTER - OSCILLATIONSEXERCISE - EXAMPLE
22 Videos
- NATURE OF PHYSICAL WORLD AND MEASUREMENTBOOK - NCERT TAMILCHAPTER - NATURE OF PHYSICAL WORLD AND MEASUREMENTEXERCISE - EXERCISE (V. Conceptual Questions)
5 Videos
- PHYSICAL WORLD BOOK - NCERT TAMILCHAPTER - PHYSICAL WORLD EXERCISE - EXERCISES
15 Videos
Similar Questions
Find the time period of oscillation of block of mass m. Spring, and pulley are ideal. Spring constant is k.

View SolutionFind the period of small vertical oscillations of a body with mass m in the system illustrated in figure. The stiffness values of the springs are x1 and x2, their masses are negligible.
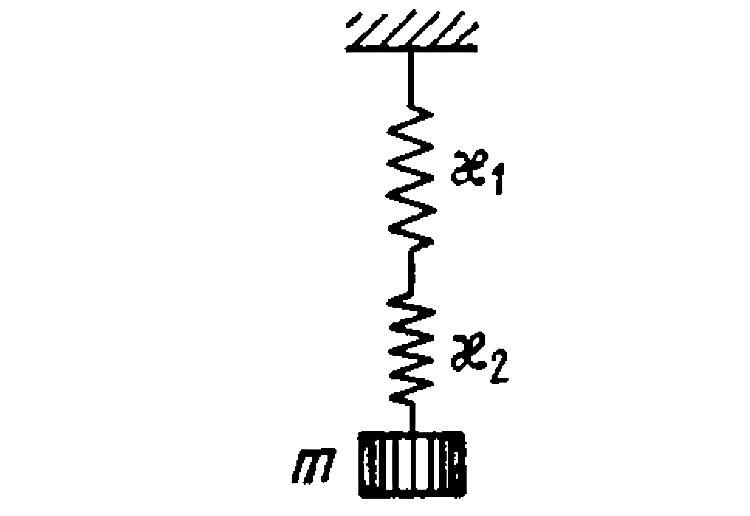
View Solution
Knowledge Check
Find the time period of oscillation of block of mass m. Spring, and pulley are ideal. Spring constant is k.
 A2π√mkBπ√mkC4π√mkD2π√m2k
A2π√mkBπ√mkC4π√mkD2π√m2kThe period of the free oscillations of the system shown here if mass m1 is pulled down a little and force constant of the spring is k and masses of the fixed pulleys are negligible, is
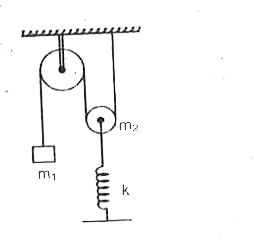 AT=2π√m1+m2kBT=2π√m1+4m2kCT=2π√4m1+m2kDT=2π√3m1+m2k
AT=2π√m1+m2kBT=2π√m1+4m2kCT=2π√4m1+m2kDT=2π√3m1+m2kIn the situation as shown in figure time period of small vertical oscillation of block will be - (String, springs and pulley are ideal)
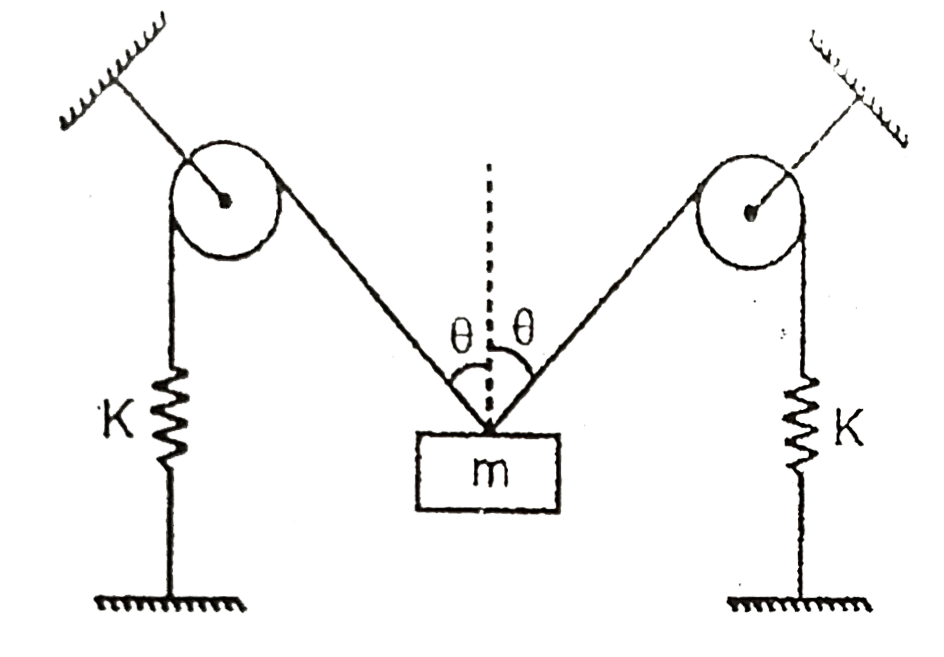 A2πcosθ√m2kB2πsecθ√m2kC2πsinθ√m2kD2πcosecθ√m2k
A2πcosθ√m2kB2πsecθ√m2kC2πsinθ√m2kD2πcosecθ√m2k
The pulley shown in figure has a moment of inertias I about its axis and mass m. find the time period of vertical oscillation of its centre of mass. The spring has spring constant k and the string does not slip over the pulley.

View SolutionThe pulley shown in figure has a moment of inertias I about its xis and mss m. find the tikme period of vertical oscillastion of its centre of mass. The spring has spring constant k and the string does not slip over the pulley.

View SolutionIn the arrangement shown in the diagram, pulleys are small and springs are ideal. k1=k2=k3=k4=10Nm−1 are force constants of the springs and mass m=10kg. If the time period of small vertical oscillations of the block of mass m is given by 2πx seconds, then find the value of x.

View SolutionIn the arrangement shown in the diagram, pulleys are small and springs are ideal. k1=k2=k3=k4=10Nm−1 are force constants of the springs and mass m=10kg. If the time period of small vertical oscillations of the block of mass m is given by 2πx seconds, then find the value of x.

View SolutionIn the situation as shown in figure time period of small vertical oscillation of block will be - (String, springs and pulley are ideal)

View Solution
